
- •Навчальний посібник
- •1 Основні принципи математичного і компютерного моделювання в сучасних екологічних дослідженнях.
- •1.1 Моделювання як методологія пізнання
- •1.2 Види моделювання
- •Математична модель – це відтворення будь-якого явища всесвіту за допомогою математичної символіки
- •1.3 Характеристики моделей
- •1.4 Особливості моделювання в екології
- •1.5 Значення моделювання в екології
- •2 Елементарні функціональні залежності в екології
- •2.1 Лінійна функціональна залежність
- •2.2 Пряма і обернена пропорціональні залежності
- •2.3 Дробово-лінійна функція. Рівняння Міхаеліса-Ментен
- •2.4 Степенева функція
- •2.5 Показникова та логарифмічна функції, їх застосування до опису розмноження популяцій
- •2.6. Тригонометричні функції та їх застосування до моделювання періодичних процесів
- •3 Моделювання екологічних cистем за допомогою диференційних рівнянь
- •3.1. Поняття похідної та її застосування до вивчення законів природи, операції диференціювання та інтегрування
- •3.2. Побудова емпіричних формул, метод найменших квадратів
- •3.3. Загальні принципи моделювання екологічних процесів за допомогою диференціальних рівнянь, стаціонарні розв'язки та їх стійкість
- •3.4 Моделювання динаміки чисельності окремих популяцій
- •5 «Жорсткі» та «м'які» математичні моделі динаміки популяцій
- •3.6 Динаміка біоценозів як наслідок міжвидових взаємовідносин
- •{Декларативна частина}
- •I,n: integer;
- •Var I,j,k: Integer;
- •I,m,n : integer;
- •Var I,j,k: Integer;
- •Var I, j : Integer;
- •11. Математичне моделювання – це моделювання,
- •12. Моделі із зосередженими значеннями (параметрами) описують …
- •Навчальний посібник
- •65082, Одеса, вул. Дворянська, 1/3
2.5 Показникова та логарифмічна функції, їх застосування до опису розмноження популяцій
2.5.1 Означення, формули і графіки
Показниковою називається функція вигляду
![]() ,
(2.5.1)
,
(2.5.1)
 де
а
-
додатне
число (а>0), що не дорівнює одиниці (а#1)
і називається
основою степеня. Показникова функція
має дійсні значення за будь-якого
значення аргументу. Тому областю
існування для неї є вся числова
вісь, тобто інтервал -∞ < х
< +∞. За будь-яких додатних чи від'ємних
значень аргументу х
значення функції у
завжди додатні, а тому її
графік всіма своїми точками лежить вище
осі Ох.
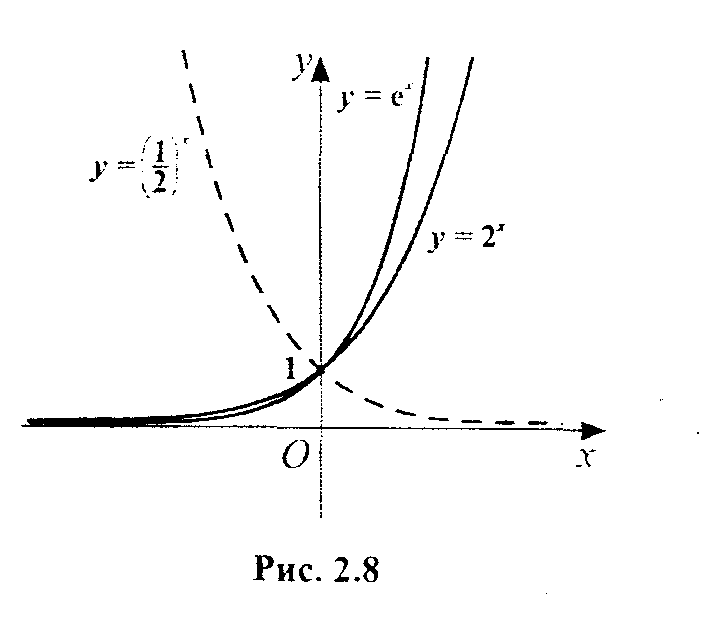
Якщо
а>1,
то
графік
являє собою криву, яка піднімається
праворуч угору (рис. 2.8).
а
якщо
а<1
то
графік є кривою, що опускається праворуч
униз (на рис.
2.8 це - пунктирна лінія). В обох випадках
вісь Ох
є
асимптотою всіх кривих,
що є графіками функції (2.6.1),
причому всі ці криві проходять через
точку (0, 1).
де
а
-
додатне
число (а>0), що не дорівнює одиниці (а#1)
і називається
основою степеня. Показникова функція
має дійсні значення за будь-якого
значення аргументу. Тому областю
існування для неї є вся числова
вісь, тобто інтервал -∞ < х
< +∞. За будь-яких додатних чи від'ємних
значень аргументу х
значення функції у
завжди додатні, а тому її
графік всіма своїми точками лежить вище
осі Ох.
Якщо
а>1,
то
графік
являє собою криву, яка піднімається
праворуч угору (рис. 2.8).
а
якщо
а<1
то
графік є кривою, що опускається праворуч
униз (на рис.
2.8 це - пунктирна лінія). В обох випадках
вісь Ох
є
асимптотою всіх кривих,
що є графіками функції (2.6.1),
причому всі ці криві проходять через
точку (0, 1).
Якщо порівняти степеневу і показникову функції, то легко побачити, що при визначенні степеневої функції за аргумент х взято основу степеня, а при визначенні показникової функції - показник степеня. Отже, обидві ці функції утворилися внаслідок введення дії піднесення до степеня. Якщо у співвідношенні (2.5.1.) за аргумент x взяти результат піднесення до степеня, а за функцію y - показник степеня, то одержимо функціональну залежність
 х
= аY
(2.5.2)
х
= аY
(2.5.2)
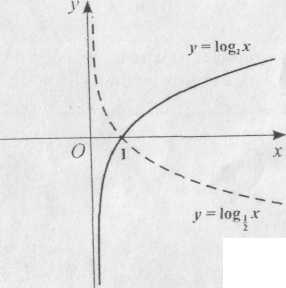
яка буде оберненою до функціональної залежності (2.5.1). Обернену до показникової функцію у називають логарифмічною і позначають її таким символом:
Рис.
2.9
![]() ,
(2.5.3)
,
(2.5.3)
де а > 0 називається основою логарифма. Рівності (2.5.2) і (2.5.3) еквівалентні й відрізняються тільки тим, що за допомогою рівності (2.5.2) можна побачити, як обчислювати значення функції, а з символічної рівності (2.5.3) цього не видно. Тому, розглядаючи рівність (2.5.3), завжди потрібно пам'ятати рівність (2.5.2), яка і є основною при визначенні логарифмічної функції. Графіки логарифмічної функції (2.5.2) або (2.5.3) мають таку саму форму, як і графіки показникової функції, але розташовані вони щодо останніх симетрично відносно бісектриси у = х першого координатного кута (рис. 2.9). Якщо в показниковій функції (2.5.1) за основу степеня а взяти число e = 2,71828 (ірраціональне число), то графік показникової функції
![]() (2.5.4)
(2.5.4)
називається експонентою (див. рис. 2.8).
Якщо в логарифмічній функції за основу логарифма а взяти число e, така функція називається натуральним логарифмом і записується так:
![]() ,
(2.5.5)
,
(2.5.5)
а якщо за основу логарифма взято а = 10, то відповідну функцію називають десятковим логарифмом і записують так:
![]() .
(2.5.6)
.
(2.5.6)
При вивченні різних природних процесів, включаючи і екологічні процеси, найчастіше зустрічаються залежності між змінними величинами, які описуються показниковою або логарифмічною функціями з основою
а = е.
2.5.2. Приклади застосування в екології
Розглянемо приклади застосування показникової і логарифмічної функцій. Розмноження більшості бактерій описується такою експоненціальною (показниковою) залежністю:
![]() ,
(2.5.7)
,
(2.5.7)
де N - кількість бактерій у будь-який час t; No - початкова кількість бактерій у момент часу t=0, r - константа швидкості розмноження бактерій, що визначається експериментально. Колонія клітин дріжджів розмножується також за експоненціальним законом. Інакше кажучи, з кожної окремої клітини через кожні десять хвилин з'являються вже дві клітини, тобто має місце їх збільшення на 100 %. Іще через десять хвилин клітин буде вже чотири, потім - вісім, шістнадцять і т. д., тобто ці числа утворюють геометричну прогресію. Таке експоненціальне зростання є звичайним процесом у біологічних, економічних та багатьох інших системах оточуючого нас світу. Проте, незважаючи на свою звичайність, експоненціальне зростання здатне приводити до досить дивних результатів, які протягом віків зачаровували людство. Всім відома стара персидська легенда про мудрого слугу, який подарував своєму королю гарну шахову дошку і попросив, щоб король натомість дав йому 1 зерно рису за першу клітинку шахової дошки, 2 зернини - за другу клітинку, 4 - за третю і т. д. Король одразу ж погодився і наказав принести рис. Для четвертої клітинки необхідно було 8 зернин, для десятої - 512, для п'ятнадцятої – 16 384, а двадцять перша клітинка принесла царському слузі понад 1 млн. зерен рису. За сорокову клітинку король повинен був віддати мільйон мільйонів зерен. Усі запаси рису в королівстві закінчились задовго до того, як дісталися шістдесят четвертої клітинки.
Отже, експоненціальне зростання, починаючи з невеликих чисел, приводить до велетенських величин, які збільшуються з блискавичною швидкістю. Таке несподіване зростання величин яскраво спостерігається ще на одному цікавому прикладі. Припустимо, що ви маєте ставок, в якому ростуть лілії. Щодня кількість квіток подвоюється. Якби дозволити ліліям розростатися безконтрольно, то вся поверхня ставка заросла б за 30 днів, знищивши при цьому всі інші форми життя у воді. Протягом досить тривалого часу заросла ліліями частина ставка залишається невеликою і немає необхідності в їх розрідженні. Тому ви вирішуєте не зрізати зайві лілії до того часу, доки вони не покриють половину ставка. На який день це відбудеться? Виходить, що половина ставка заросте на двадцять дев'ятий день. Отже, для спасіння ставка залишається тільки один день.
 На
рис. 2.10 зображена крива експоненціального
зростання
кількості
населення світу. В 1650 році чисельність
Рис.
2.10
населення Землі становила
приблизно
0,5 млрд. чол. і збільшувалась з темпом
зросгання 0,3 % на
рік. Це відповідає періоду подвоєння
кількості населення, рівному приблизно
250 рокам. У 1970 році загальна чисельність
населення Землі становила
3,6 млрд. чол., а темп зростання дорівнював
2,1 % на рік. При такому
темпі збільшення населення період його
подвоєння дорівнює 33
рокам. Отже, бачимо, що чисельність
населення зростає не просто експоненціально,
а таким чином, що збільшується сам темп
зростання. У
даному випадку можна говорити про
понадекспоненціальне зростання
населення,
тобто крива чисельності населення
піднімається швидше, ніж це
мало б місце при експоненціальному
зростанні.
На
рис. 2.10 зображена крива експоненціального
зростання
кількості
населення світу. В 1650 році чисельність
Рис.
2.10
населення Землі становила
приблизно
0,5 млрд. чол. і збільшувалась з темпом
зросгання 0,3 % на
рік. Це відповідає періоду подвоєння
кількості населення, рівному приблизно
250 рокам. У 1970 році загальна чисельність
населення Землі становила
3,6 млрд. чол., а темп зростання дорівнював
2,1 % на рік. При такому
темпі збільшення населення період його
подвоєння дорівнює 33
рокам. Отже, бачимо, що чисельність
населення зростає не просто експоненціально,
а таким чином, що збільшується сам темп
зростання. У
даному випадку можна говорити про
понадекспоненціальне зростання
населення,
тобто крива чисельності населення
піднімається швидше, ніж це
мало б місце при експоненціальному
зростанні.
Але для більшості біологічних процесів, в тому числі й процесу розмноження різних популяцій, значення змінних не можуть зростати необмежено. Для опису таких процесів добре пристосована показникова функція з від'ємним показником
![]() .
(2.5.8.)
.
(2.5.8.)
Чисельність більшості популяцій спочатку зростає, а потім ріст припиняється і чисельність залишається сталою, точніше, не перевищує певної величини Nmax. Таку динаміку чисельності популяції можна описати за допомогою функції
![]() ,
(2.5.9)
,
(2.5.9)
де N0 - початкова чисельність популяції, k - постійне число (коефіцієнт) яке визначається експериментально для кожного виду популяції.
Прямі N = Nmax є горизонтальною асимптотою графіка цієї функції (рис. 2.11), де величина Nmax називається ємністю середовища.
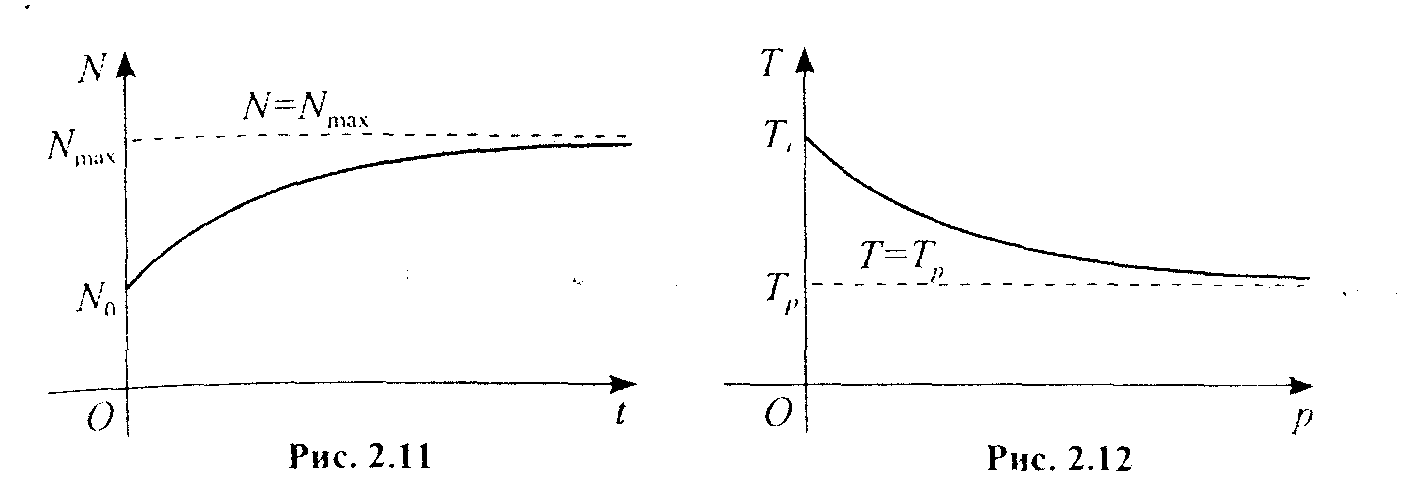
Розглянемо ще один приклад, пов'язаний з дією на організм тварин шкідливих речовин (токсикантів), які скорочують тривалість їхнього життя. Якшо дозу речовини, що діє на організм, позначити через р, середню тривалість життя контрольних тварин - через Тs, і врахувати дію великої кількості токсичних речовин (р→∞), що скорочує тривалість житія Т до величини Тр, то процес дії шкідливої речовини добре описується такою показниковою функцією з від'ємним показником:
![]() (2.5.10)
(2.5.10)
Графік функції (2.6.10) мас горизонтальну асимптоту Т = Tp (рис. 2,12), сталі Тр і k визначаються експериментально для кожного виду тварин і для кожної шкідливої речовини.
На сам кінець наведемо приклад, в якому для математичного моделювання процесів збільшення ваги риби застосовується комбінація показникової і степеневої функцій. Бевертон і Холт запропонували визначати вагу риби будь-якого віку за допомогою формули Берталанфи :
![]() ,
(2.5.11)
,
(2.5.11)
де Wmax -найбільша вага риби, а і t0 – емпіричні коефіцієнти (графік цієї функції читач легко побудує самостійно).
