
- •Навчальний посібник
- •1 Основні принципи математичного і компютерного моделювання в сучасних екологічних дослідженнях.
- •1.1 Моделювання як методологія пізнання
- •1.2 Види моделювання
- •Математична модель – це відтворення будь-якого явища всесвіту за допомогою математичної символіки
- •1.3 Характеристики моделей
- •1.4 Особливості моделювання в екології
- •1.5 Значення моделювання в екології
- •2 Елементарні функціональні залежності в екології
- •2.1 Лінійна функціональна залежність
- •2.2 Пряма і обернена пропорціональні залежності
- •2.3 Дробово-лінійна функція. Рівняння Міхаеліса-Ментен
- •2.4 Степенева функція
- •2.5 Показникова та логарифмічна функції, їх застосування до опису розмноження популяцій
- •2.6. Тригонометричні функції та їх застосування до моделювання періодичних процесів
- •3 Моделювання екологічних cистем за допомогою диференційних рівнянь
- •3.1. Поняття похідної та її застосування до вивчення законів природи, операції диференціювання та інтегрування
- •3.2. Побудова емпіричних формул, метод найменших квадратів
- •3.3. Загальні принципи моделювання екологічних процесів за допомогою диференціальних рівнянь, стаціонарні розв'язки та їх стійкість
- •3.4 Моделювання динаміки чисельності окремих популяцій
- •5 «Жорсткі» та «м'які» математичні моделі динаміки популяцій
- •3.6 Динаміка біоценозів як наслідок міжвидових взаємовідносин
- •{Декларативна частина}
- •I,n: integer;
- •Var I,j,k: Integer;
- •I,m,n : integer;
- •Var I,j,k: Integer;
- •Var I, j : Integer;
- •11. Математичне моделювання – це моделювання,
- •12. Моделі із зосередженими значеннями (параметрами) описують …
- •Навчальний посібник
- •65082, Одеса, вул. Дворянська, 1/3
2.6. Тригонометричні функції та їх застосування до моделювання періодичних процесів
2.6.1 Означення та графіки
Тригонометричні функції виражають залежність між відношеннями сторін прямокутного трикутника та його гострими кутами. Якщо розглянути прямокутний трикутник ABC з катетами а і b та гіпотенузою с (рис. 2.13, а), то можна формулювати означення тригонометричних функцій гострого кута А таким чином:
синусом кута А називається відношення протилежного катета а до гіпотенузи с:
![]() ;
(2.6.1)
;
(2.6.1)
косинусом кута А називається відношення прилеглого катета b до гіпотенузи с:
![]() ;
(2.6.2)
;
(2.6.2)
тангенсом кута А називається відношення протилежного катета а до прилеглого катета b:
![]() ;
(2.6.3)
;
(2.6.3)
котангенсом кута А називається відношення прилеглого катета b до протилежного катета а:
![]() (2.6.4)
(2.6.4)
Кути вимірюються градусами і радіанами (рис. 2.13, б).
Радіаном називається гострий кут , під яким видно з центра кола 0 дугу MN, довжина якої дорівнює радіусу R (MN = ОМ = R).
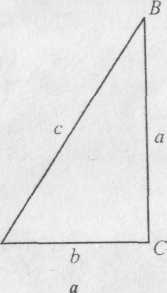
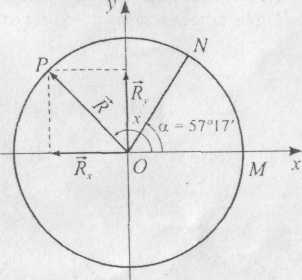
Рис. 2.13
Оскільки півколо видно з центра кола під кутом 180°, а довжина його дорівнює R, де R - радіус кола (рис. 2.13, б), то розгорнутий кут, що дорівнює 180°, має радіанів. Отже, між градусами і радіанами існує така залежність:
![]() ;
(2.6.5)
;
(2.6.5)
![]() ;
(2.6.6)
;
(2.6.6)
![]() .
(2.6.7)
.
(2.6.7)
Для довільного кута х тригонометричні функції визначаються рівностями
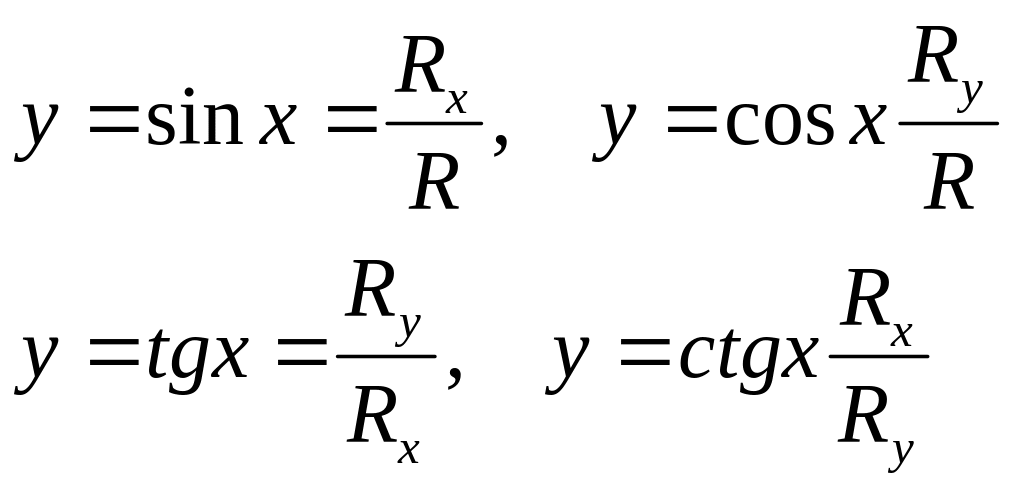 (2.6.8)
(2.6.8)
де
х
-
кут, утворений радіусом-вектором
![]() з додатним напрямом осі абсцис Ох
(рис.
2.13, б),
R
- довжина
(модуль) радіуса-вектора
з додатним напрямом осі абсцис Ох
(рис.
2.13, б),
R
- довжина
(модуль) радіуса-вектора
![]() , Rх:
і
Rу
- його
координати (проекції відповідно на вісі
Ох
та
Оу).
, Rх:
і
Rу
- його
координати (проекції відповідно на вісі
Ох
та
Оу).
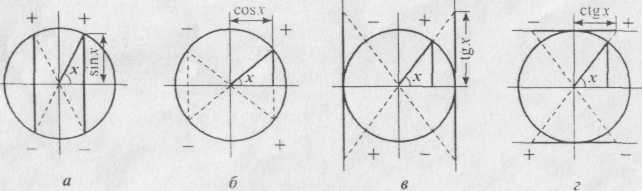 Рис 2.14
Рис 2.14
Значення
тригонометричних функцій будь-якого
кута х
можна
зобразити
геометрично у вигляді відрізків відносно
кола, радіус якого дорівнює одиниці, а
центр розміщений у точці О
- початку
координат. На рис. 2.14
зображені
значення тригонометричних функцій у
різних чвертях (квадрантах):
на рис. 2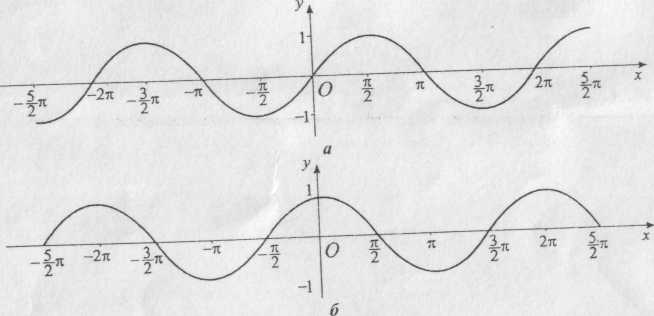 .14,
а
зображені
значення синуса, на рис. 2.14, б
- значення
косинуса,
.14,
а
зображені
значення синуса, на рис. 2.14, б
- значення
косинуса,
на рис. 2.14, в - значення тангенса, а на рис. 2.14, г - значення котангенса
Рис. 2.15
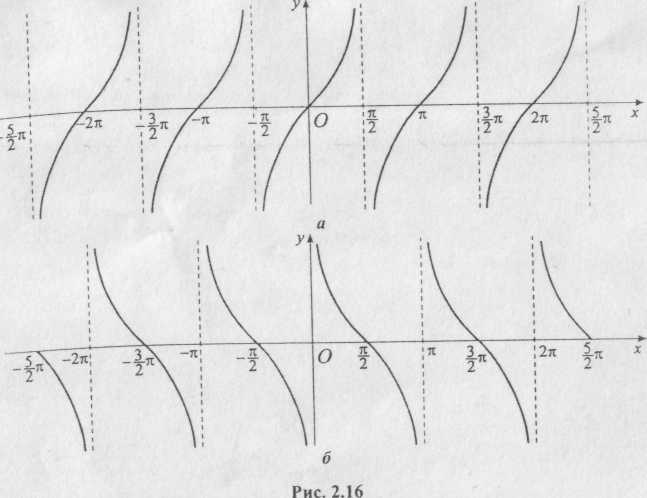
Використовуючи добре відомі значення тригонометричних функцій для певних значень аргументів (кутів), що представлені в табл. 2.1, легко побудувати графіки цих функцій, які називаються синусоїдою і косинусоїдою (рис. 2.15) та тангенсоїдою і котангенсоїдою (рис. 2.16).
Таблиця 2.1
У |
α° |
|||||||
0° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
|
sin х |
0 |
|
|
|
1 |
0 |
–1 |
0 |
cos х |
1 |
|
|
|
0 |
–1 |
0 |
1 |
tg х |
0 |
|
1 |
|
±∞ |
0 |
±∞ |
0 |
ctg х |
∞ |
|
1 |
|
0 |
±∞ |
0 |
±∞ |
У |
0 |
|
|
|
|
π |
|
2π |
х |
||||||||
2.6.2 Основні співвідношення
Характерною властивістю тригонометричних функцій є їх періодичність.
Функція називається періодичною, якщо існує таке число h, що додавання його до будь-якого значення аргументу не змінює значення функції.
Інакше кажучи, періодичними називаються такі функції, для яких виконується рівність
![]() . (2.6.9)
. (2.6.9)
Найменше з чисел h називається періодом функції і позначається через . Інколи число називають основним періодом.
З графіків видно, що основний період функцій sin х і cos х дорівнює 2, а основний період функцій tg x і ctg де дорівнює .
Якщо синусоїдальну (гармонічну) функціональну залежність записати в такому вигляді
![]() ,
(2.6.10)
,
(2.6.10)
то стала А - це амплітуда, > 0 - частота, сума (t + ) - фаза, а – початкова фаза (вона одержується з фази при t = 0).
Амплітуда збільшує висоту синусоїди в А разів, а частота перетворює період 2 на період , що дорівнює
![]() ,
(2.6.11)
,
(2.6.11)
тобто зменшує період 2 у ) разів.
За
наявності початкової фази
(або -)
синусоїда змішується вліво
(вправо)
на величину
![]() .
.
З означень тригонометричних функцій, тобто з формул (2.6.1)–(2.6.4) випливають такі важливі співвідношення:
![]() ;(2.6.12)
;(2.6.12)
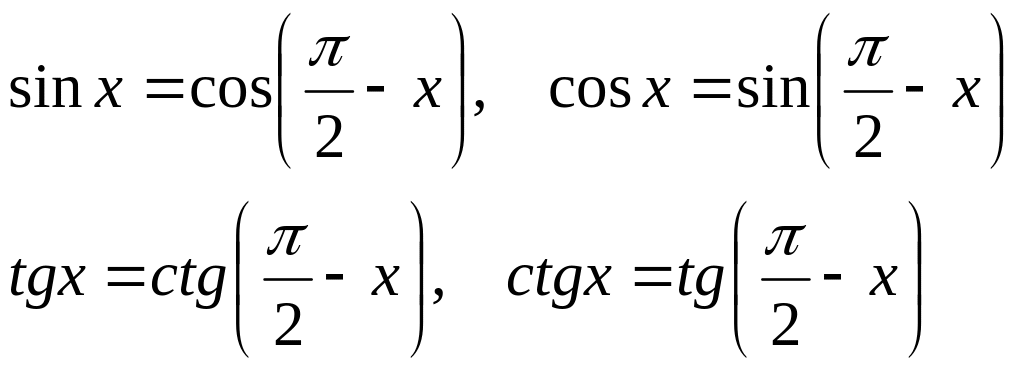 .(2.6.13)
.(2.6.13)
Для прямокутного трикутника АВС (див. рис. 2.13, а) виконується теорема Піфагора, а саме:
![]() . (2.6.14)
. (2.6.14)
Якщо ліву і праву частини рівності (2.6.14) розділити на с2, то одержимо
![]() .
(2.6.15)
.
(2.6.15)
Враховуючи співвідношення (2.6.1) і (2.6.2), з (2.6.15) одержимо основну тригонометричну тотожність:
![]() .
(2.6.16)
.
(2.6.16)
З тотожності (2.6.16) випливають такі співвідношення
![]() ;
(2.6.17)
;
(2.6.17)
![]() .
(2.6.18)
.
(2.6.18)
Якщо ввести означення ще двох тригонометричних функцій, а саме, секанса і косеканса:
![]() ,
(2.6.19)
,
(2.6.19)
то формули (2.6.18) перепишуться у такому вигляді:
![]() .
.
2.6.3 Моделі періодичних процесів
Розглянемо приклади застосування тригонометричних функцій до моделювання періодичних процесів, що спостерігаються в природі. Взагалі, точних (строгих) періодичних процесів у природі не дуже багато, але близькі до періодичних (майже періодичних або квазіперіодичних) спостерігаються досить часто. Зокрема, зміна температури повітря, води в річках та поверхні Землі відбувається по роках, по сезонах і протягом доби. Нехай відомо, що літньої днини найвища температура повітря, яка дорівнює 25 °С, досягається опівдні, а найнижча температура, що дорівнює 15 °С, спостерігається опівночі, тобто в нуль годин (або о 24 годині). Покажемо, що цей процес зміни температури Т протягом доби можна наближено описати такою тригонометричною функцією:
![]() ,
(2.6.20)
,
(2.6.20)
де через t позначено час в годинах, 0 t 24.
У
розглянутому випадку, коли
![]() ,
маємо, що період зміни температури
повітря дорівнює
,
маємо, що період зміни температури
повітря дорівнює
![]() .
(2.6.21)
.
(2.6.21)
Графік функції (2.6.20) побудуємо в такій послідовності:
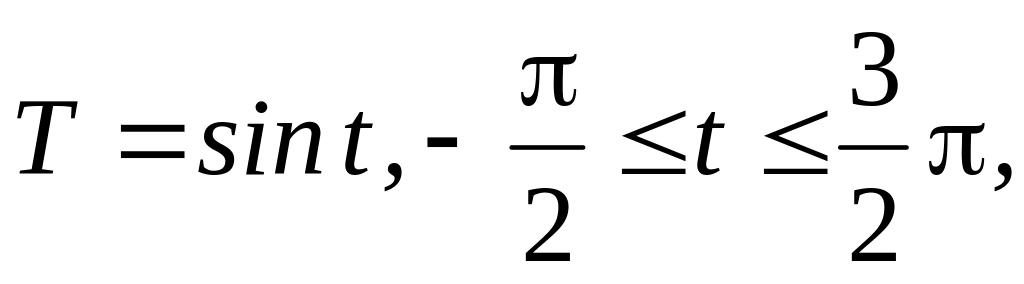 ,
графік на рис. 2.17, а;
(2.6.22)
,
графік на рис. 2.17, а;
(2.6.22)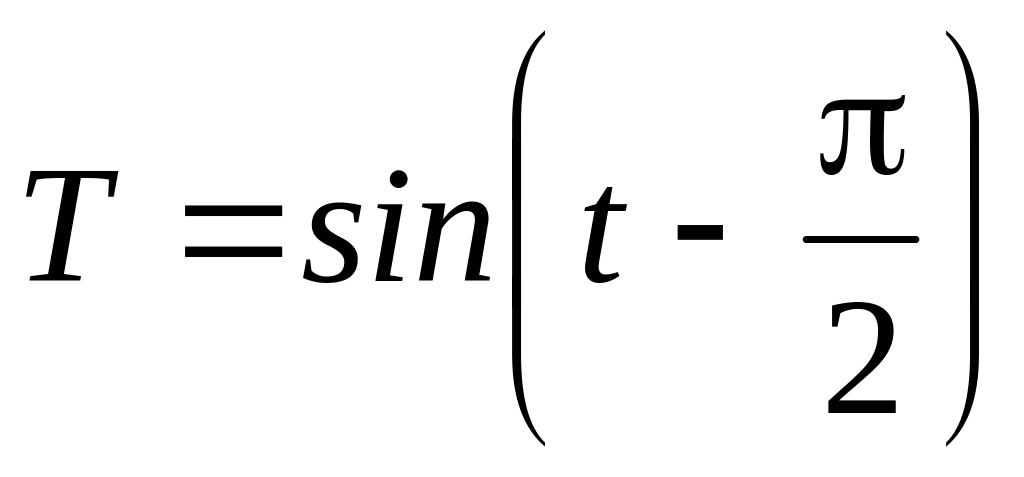 ,
графік на рис. 2.17, б;
(2.6.23)
,
графік на рис. 2.17, б;
(2.6.23)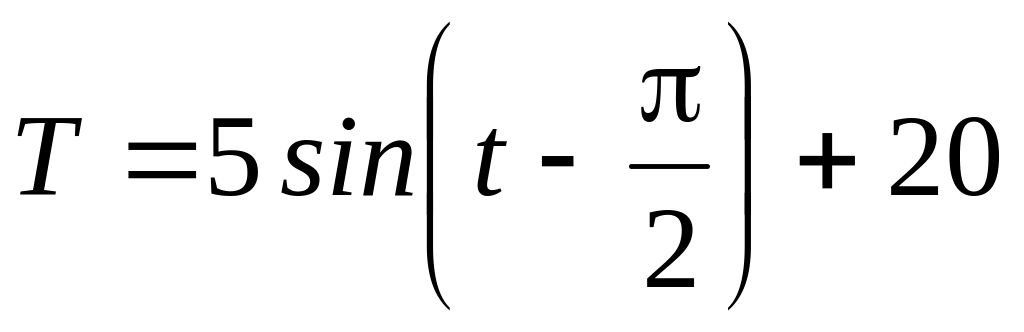 ,
графік на рис. 2.17, в;
(2.6.24)
,
графік на рис. 2.17, в;
(2.6.24)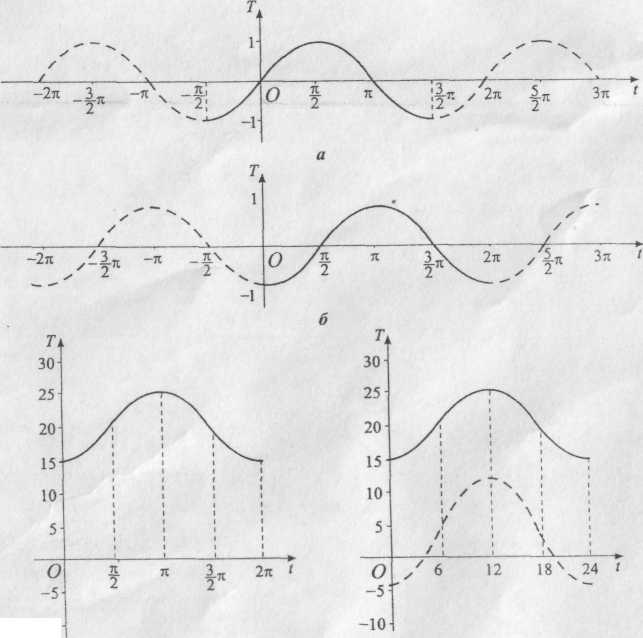
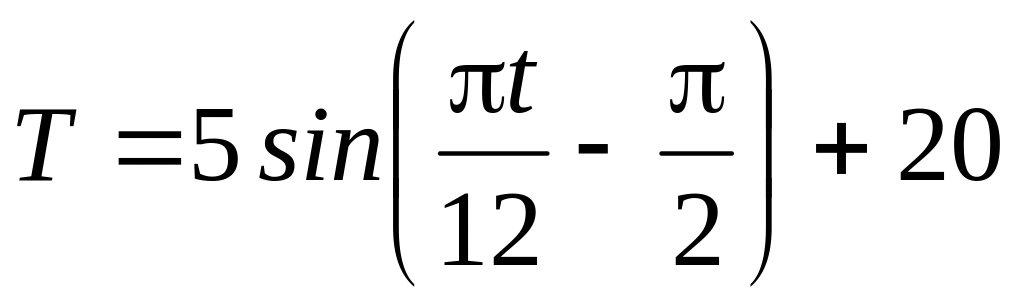 ,
графік на рис. 2.17, г;
(2.6.25)
,
графік на рис. 2.17, г;
(2.6.25)
Рис 2.17
Функцію (2.6.20) можна визначити іншим способом. Для цього скористаємося загальним виглядом функції
![]() (2.6.26)
(2.6.26)
та додатковими умовами, що випливають з постановки задачі, а саме:
![]() .
(2.6.27)
.
(2.6.27)
З умов (2.6.27) видно, що функція (2.6.26) повинна мати період 24, мінімальне значення її дорівнює 15, а максимальне - 25. Скориставшись залежністю (2.6.11), знаходимо частоту
![]() .
(2.6.28)
.
(2.6.28)
Враховуючи,
що синус набуває найменшого значення
при
![]() ,
знаходимо початкову фазу
,
знаходимо початкову фазу
![]() .
(2.6.29)
.
(2.6.29)
Отже, шукана функція має такий вигляд:
![]() .
(2.6.30)
.
(2.6.30)
Тепер, якщо скористатися умовами (2.6.27), то одержимо таку систему рівнянь:
![]() (2.6.31)
(2.6.31)
Розв'язавши систему (2.6.31), знаходимо невідомі параметри А і В:
![]() .
(2.6.32)
.
(2.6.32)
Підставивши значення (2.6.32) у рівність (2.6.29), шукану функцію запишемо в такому остаточному вигляді:
![]() .
(2.6.33)
.
(2.6.33)
Якщо протягом доби температура повітря змінюється від -4 °С до 12 °С, то для визначення сталих А і 5 одержимо таку систему рівнянь:
![]() (2.6.34)
(2.6.34)
Розв'язавши систему (2.6.34), знайдемо:
![]() .
(2.6.35)
.
(2.6.35)
Підставивши (2.6.35) в (2.6.30), отримаємо нову функцію такого вигляду (графік зображений на рис. 2.17, г пунктирною лінією):
![]() .
(2.6.36)
.
(2.6.36)
Подібним способом за допомогою тригонометричних функцій описуються також інші періодичні процеси.
