3.4 Моделювання динаміки чисельності окремих популяцій

3.4.1. Експоненціальний закон

Розглянемо, як будуються найпростіші математичні моделі, що вперше почали застосовуватись у біології та екології (моделі, що були запропоновані В. Вольтерою і А. Лоткою [3] для описування розвитку популяцій при взаємодії типу «хижак - жертва» розглядатимуться у підпункті 3.6.2. Нагадаємо, що популяцією називають будь-яку групу організмів одного виду, що протягом великого числа поколінь займає певний простір і може функціонувати (розмножуватись і розвиватись) за певних умов навколишнього природного середовища. Популяція - це елементарна одиниця еволюційного процесу і форма існування виду, це множина (група) організмів, що мають властивість саморозмноження.

Популяції мають властивості, притаманні як самій популяції (щіль­ність, народжуваність, смертність, вікова структура, генетика, пристосованість), так і окремим організмам (життєвий цикл, репродукція та ін.).

Біотичне угруповання, в свою чергу, визначається як сукупність популяцій, що функціонує як цілісна одиниця у відведеному йому просторі фізичного природного середовища.

Під щільністю популяції розуміють число особин (організмів) на одиницю площі або об'єму, наприклад 500 дерев на га, 200 кг риби на га або 5 млн діатомей на м³ води. Якщо знехтувати віковими, статевими і генетичними відмінностями, то щільність певного виду досліджуваних організмів може бути повністю математично описана однією змінною величиною - числом особин на одиницю площі. Всі популяції дуже мінливі, тобто їх чисельність (щільність) з часом зазнає змін. Навіть у тому випадку, коли угруповання (популяція) та екосистема вбачаються незмінними, щільність, народжуваність, рівень виживання (смертність), вікова структура, швидкість росту та інші характеристики, як правило, змінюються залежно від зміни сезону, клімату та інших факторів навколишнього середовища. Екологів найбільше цікавить те, з якою швидкістю відбувається зміна чисельності популяції або її певної вікової групи. Середня швидкість розмноження популяції визначається як відношення зміни кількості організмів (особин) N до проміжку часу t, протягом якого відбулася ця зміна (збільшення або зменшення, в останньому випадку N береться зі знаком

мінус). Миттєва (істинна) швидкість розмноження особин або просто швидкість розмноження організмів у деякий момент часу t визначається як межа середньої швидкості за умови необмеженого зменшення проміжку часу t, тобто:

(3.4.1)

Таким чином, швидкість розмноження популяції є похідною за часом від кількості особин, що розглядається як функція часу (віку особин або віку популяції), тобто N = (t), V = '(t).

Крім уже згаданих кількісних величин, при формалізації закономірно­стей розмноження популяцій розглядають також певну так звану питому швидкість розмноження г, яка дорівнює зміні числа особин за одиницю часу з розрахунку на одну особину (організм), тобто:

(3.4.2)

Якщо розглядати випадок, коли для розмноження популяції створені найсприятливіші умови і відсутні лімітуючі фактори, то швидкість зростання чисельності популяції може бути описана диференціальним рівнянням

(3.4.3)

що виражає закон прямої пропорційності швидкості розмноження кількості особин (організмів) цієї популяції, причому параметр r в рівнянні (3.4.3) часто називають коефіцієнтом швидкості розмноження популяції (або угруповання). Рівняння (3.4.3) вперше в 1802 р. одержав англійський священик Томас Мальтус. Помилка Мальтуса полягала в тому, що він це рівняння, яке справедливе для певного класу популяцій (про що йтиметься далі), вважав універсальним законом не тільки для всієї природи, але й для суспільства людей.

Для розв'язання (інтегрування) диференціального рівняння (3.4.3) розділимо в ньому змінні N і t, а саме:

Після інтегрування одержимо

З останньої рівності після потенціювання одержимо:

Якщо відома чисельність популяції N = N₀ в початковий момент часу t =t₀, то, підставивши в останню рівність ці значення, одержимо:

Отже, після розв'язання (інтегрування) рівняння (3.4.3) знаходимо шу­кану функцію у такому вигляді:

(3.4.4.)

де N_о — чисельність популяції у початковий момент часу t =t₀, е = ехр - основа натуральних логарифмів, число е дорівнює = 2,718282... ≈ 2,72 .

Для визначення коефіцієнта r (питомої швидкості розмноження) необхідно прологарифмувати обидві частини рівності (3.4.4) і записати це так:

(3.4.5.)

Користуючись рівнянням (3.4.5), можна обчислити значення r за двома відомими значеннями величин N₁, і N₂ у будь-які два моменти часу t₀=t₁ і t₂

(3.4.6)

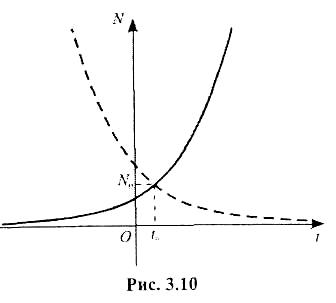
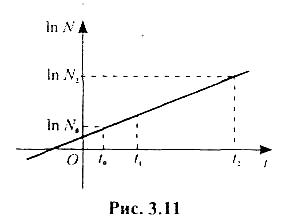
Експоненціальна функція (3.4.4) добре описує розмноження (зростання) колоній деяких бактерій до виснаження культурального середовища (їжі). Графік цієї функції називається кривою зростання (розмноження) популяції (рис. 3.10). Число особин, що визначається цією кривою (рис. 3.10), можна також зобразити відповідно до рівності (3.4.5) в логарифмічному масштабі (рис. 3.11).

З іншого боку, питому швидкість розмноження - параметр r - можна біологічно інтерпретувати як різницю між питомою швидкістю народження «b» (birth) і питомою швидкістю смертності « d» (death).

r = b - d (3.4.7)

Показник r часто використовують для кількісної характеристики репродуктивної пристосованості організмів у генетичному розумінні і називають біотичним потенціалом, тобто цей показник (параметр) характеризує вроджену властивість організмів до розмноження та виживання. За природних умов у короткочасні періоди, коли мається достатньо їжі, відсутні скупченість і хижаки-вороги, для популяцій часто проявляється експоненціаль­ний характер зростання чисельності. За таких умов уся популяція зростає з величезною швидкістю, хоча при цьому кожен організм розмножується з постійною швидкістю (питома швидкість розмноження є сталою r = const) .

Багато явищ природи, такі як «цвітіння» води у водоймищах, спалах (вибух) чисельності шкідників, розмноження бактерій та інших мікроорганізмів, супроводжується зростанням чисельності організмів згідно з експоненціальним законом. За сприятливих неконтрольованих умов потомство однієї пари мух через кілька років важило б більше, ніж земна куля [3]. Відзначимо також, що експоненціальний характер спостерігається для багатьох інших процесів і явищ природи, таких як поглинання світла, мономолекулярні хімічні реакції, зростання складних процентів та ін. Проте, як уже було зазначено, сприятливі для розмноження умови не можуть довго існувати через вплив навколишнього середовища, присутність ворогів (хижаків) та інших несприятливих для життя тої чи іншої популяції факторів. Взаємодія популяції з іншими та вплив зовнішнього середовища значно зменшує швид­кість зростання її чисельності і змінює характер закономірності розмноження цієї популяції (або угруповання). Зокрема, якщо питома швидкість смертності d перевищує питому швидкість народження b, то величина r = b - d. буде від'ємною і розв'язок рівняння (3.4.3) запишеться у такому вигляді:

народження b, то величина r = b - d. буде від'ємною і розв'язок рівняння (3.4.3) запишеться у такому вигляді:

(3.4.8)

Графік функції (3.4.8) буде спадною кривою з асимптотою N = 0 (на рис. 3.10 пунктирна лінія).

3.4.2 Логістичне рівняння

Отже, оскільки після інтенсивного зростання чисельність популяції може стабілізуватися на деякому стійкому рівні, то в даному разі доцільно зростання чисельності (розмноження) популяції описувати так званим логістичним рівнянням:

яке часто записується в такому вигляді

(3.4.10)

де через r, як уже зазначалось, позначено питому швидкість розмноження, а через K = N_max - максимально можливу чисельність популяції (угруповання). На відміну від лінійного диференціального рівняння (3.4.3), рівняння (3.4.9) є нелінійним диференціальним рівнянням, а нелінійні залежності краще описують реальні об'єкти. З іншого боку, нелінійні моделі складніші, і тому їх аналіз має певні, часом досить значні труднощі. Розділивши змінні в рівнянні (3.4.10), одержимо рівняння:

(3.4.11)

Яке, враховуючи співвідношення

(3.4.12)

Запишемо у такому вигляді

(3.4.13)

Після інтегрування рівняння (3.4.13) одержимо

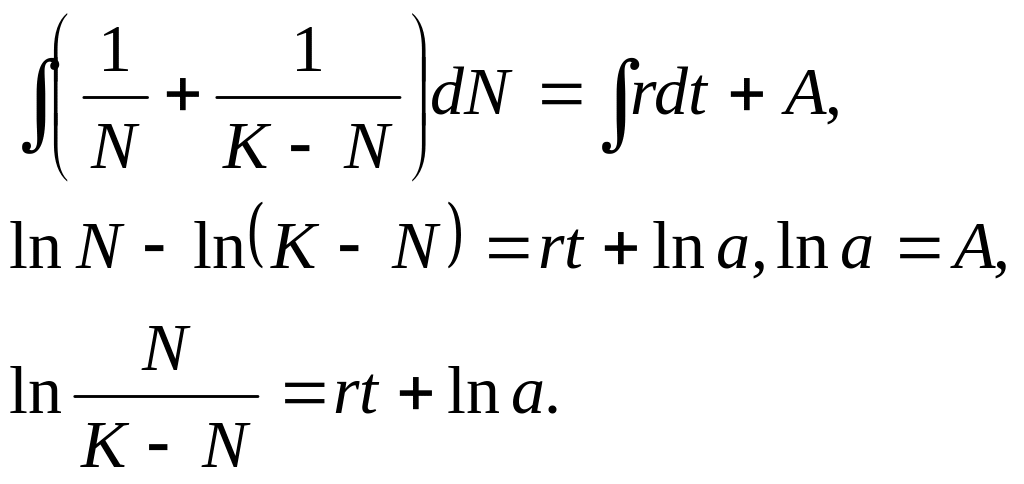
З останньої рівності знаходимо

(3.4.14)

Якщо відомо, що при t = 0 число особин було N = N₀, то за допомогою рівності (3.4.14) знайдемо параметр а:

(3.4.15)

Розв'язавши рівняння (3.4.14) відносно N, знайдемо шукану функцію N = f(t) у такому вигляді:

(3.4.16)

або після ділення чисельника і знаменника правої частини на е^rt одержимо:

(3.4.17)

Функцію (3.4.17) можна записати і в такому вигляді:

(3.4.18)

де стала інтегрування b визначається рівністю:

(3.4.19)

Розв'язок (3.4.18) логістичного рівняння (3.4.10) зображається сигмовидною кривою, яка називається логістичною кривою (рис. 3.12). Асимптотою кривої є пряма N = К.

Логістичне рівняння вперше було запропоноване Ферхюльстом в 1838 р. Ним також користувався Лотка, а потім майже через 100 років його «перевідкрили» Перл і Рід. Рівняння Ферхюльста-Перла (3.4.9) враховує так званий ефект самоотруєння популяції, або точніше, внутрішню боротьбу (конкуренцію) в популяції, яка описується членом - .

Розв'язок (3.4.18)—(3.4.19) має дві важливі властивості:

1. при малих значеннях чисельності (або біомаси) популяції зростання відбувається за експоненціальним законом, як і у випадку рівняння (3.4.4);

2. з часом чисельність популяції асимптотично наближається до деякого постійного числа К, перевищити яке чисельність популяції не може (число К називається ємністю середовища).

Потрібно зазначити, що більшість біологічних процесів за сприятли­вих і стабільних природних умов дуже добре описується логістичним рівнянням, причому максимальний рівень розмноження популяції визначається ємністю середовища К, а швидкість розмноження (крутість сигмоподібної кривої і положення точки перегину М_о) залежить від величини r = b - d (рис. 3.12).