3.6 Динаміка біоценозів як наслідок міжвидових взаємовідносин

3.6.1 Основні типи взаємовідносин

Під біоценозом, як правило, розуміють угруповання таких популяцій біологічних видів, які взаємодіють між собою і беруть істотну участь у функціонуванні екосистеми. В біоценоз включаються не тільки ті види рослин, тварин і мікроорганізмів, які постійно мешкають у даній екосистемі, а й види, що проживають у ній тільки певний час свого життєвого циклу, але істотно впливають на стан екосистеми. Представники кожного виду здатні існувати лише в такому біотичному оточенні, де зв'язки з іншими організмами забезпечують їм нормальні умови життя. Серед величезного розмаїття взаємовідносин живих істот можна виділити певні типи відносин, які найчастіше зустрічаються у середовищі організмів, популяцій і біоценозів. Саме знання цих типів взаємовідносин дозволяє вивчати динаміку популяцій за допомогою математичного моделювання.

Як уже не раз підкреслювалось, при побудові математичних моделей насамперед застосовуються ті закони і співвідношення, які важко заперечувати і які певною мірою мають абсолютний характер. Останнім часом при побудові моделей біологічних угруповань (біоценозів) різних видів організмів широко використовується добре відома в екології така класифікація взаємовідносин між видами.

1. Хижацтво (+,-): один вид («хижак») пригнічує розвиток іншого виду («жертви»), а інший вид («жертва») прискорює розвиток першого («хижака»).

2. Конкуренція (-,-): кожен з видів має пригнічуючий (негативний) вплив на розвиток іншого виду, хоча існує і внутрішньовидова конкуренція.

3. Симбіоз (+,+) або коменсалізм (+,0): кожен з видів прискорює зростання (розвиток) іншого або один вид дістає вигоду, не завдаючи іншому шкоди, але й не приносячи користі.

Якщо розвиток (розмноження) однієї популяції можна, як уже було показано, описати експоненціальним або логістичним рівнянням, тобто одним з рівнянь

(3.6.1)

то вплив іншої популяції можна описати ще одним додатковим членом, який змінює розвиток першої популяції.

Вигляд цього члена рівняння залежить від виду взаємовідносин між популяціями.

Нехай маємо дві популяції чисельністю N₁, і N₂, які взаємодіють між собою. Розмноження кожної з цих популяцій будемо описувати логістич­ним рівнянням, а їхню взаємодію опишемо членом, пропорціональним добутку N₁ N₂. Тоді, у випадку взаємовідносин типу «хижацтво» динаміка популяцій опишеться такою системою диференціальних рівнянь:

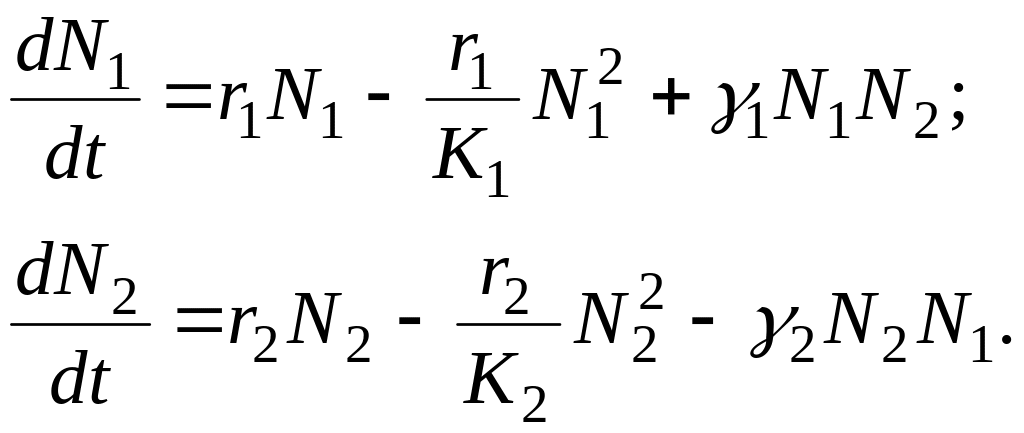
У випадку взаємовідносин типу «конкуренція» динаміка популяцій опишеться

системою:

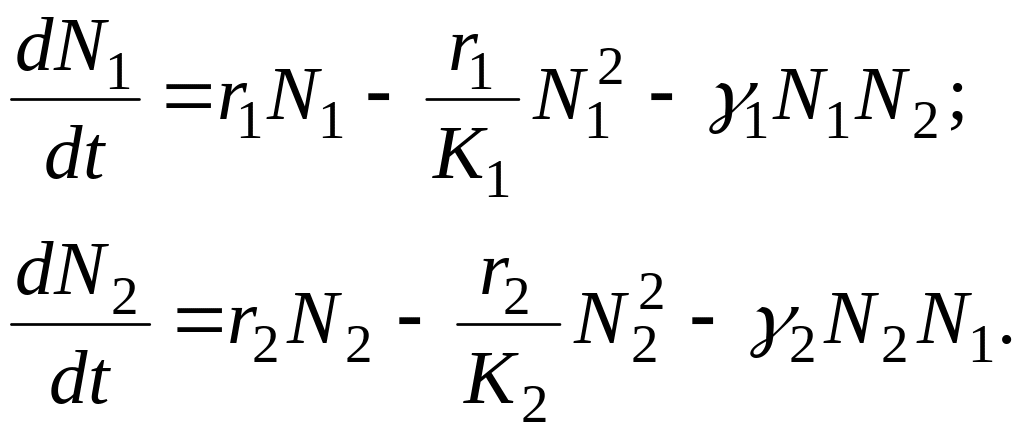
У випадку взаємовідносин типу «cимбіоз» динаміка популяцій опи­шеться системою:

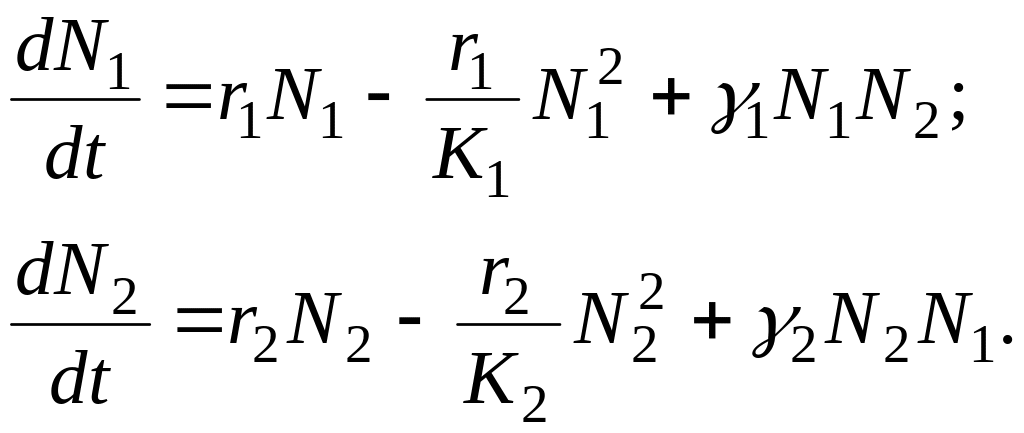
3.6.2. Математичні моделі популяцій при взаємовідносинах «хижак — жертва

Перевага наведеної класифікації взаємовідносин в її простоті й логічності. Використовуючи її, розглянемо найпоширенішу в природі систему двох популяцій (або видів). Особини однієї з них стають їжею для особин іншої, тобто маємо взаємодію типу «хижак - жертва». Крім балансових рівнянь чисельності або біомас, що одержуються згідно із законом збереження речовин (або енергії), необхідно ще знати швидкості споживання жертви хижаком (швидкість виїдання), яка звичайно зале­жить як від кількості жертв, так і від кількості хижаків. Цю залежність в екології, зокрема в гідроекології, називають трофічною функцією або трофічним коефіцієнтом. Зрозуміло, що вигляд цієї функції залежить від багатьох факторів, передусім таких, як: мисливська стратегія хижака, захисна реакція жертви, наявність схованок для жертви тощо.

Вперше диференціальне рівняння (математична модель), що описує взаємодію «хижак - жертва», було одержано італійським математиком Віто Вольтерра [2], якого не випадково називають батьком математичної екології. Рівняння, як правило, складається відносно чисельності популяції або відносно біомаси організмів. Розглянемо найпростіші і найпоширеніші з них, лінійні диференціальні рівняння.

Позначимо чисельність (або біомасу) однієї популяції («жертви») через В. а іншої популяції («хижака») - через Р. Спочатку розглянемо випадок, коли хижак розмножується за експоненціальним законом і впливає на жертву, яка має доступ до сталого запасу харчів. У даному разі динаміку взаємодії даних популяцій можна описати такою системою лінійних диференціальних рівнянь:

(3.6.2)

(3.6.3)

де α₁ - коефіцієнт засвоєння їжі «жертвою», т₁,т₂ — коефіцієнти смертності відповідно «жертви» і «хижака», «жертви» «хижаком» та коефіцієнт засвоєння їжі «хижаком».

(3.6.4)

Враховуючи розв’язок (3.6.4), рівняння (3.6.2) запишемо у вигляді:

(3.6.5)

Щоб знайти розв’язок неоднорідного лінійного рівняння (3.6.5), скористаємось розв’язком відповідного лінійного однорідного рівняння:

(3.6.6)

Яке запишемо у вигляді:

(3.6.7)

Розв'язок неоднорідного рівняння (3.6.5) шукатимемо методом варіації сталої (метод Лагранжа) тобто загальний розв'язок визначатимемо за таким рівнянням:

(3.6.8)

де А(t) – таким, що невідома функція. Знайдемо похідну:

(3.6.9)

Підставивши (3.6.8) і (3.6.9) рівняння (3.6.5), одержимо:

Або,

(3.6.10)

Після вирахування рівняння (3.6.10) одержимо:

(3.6.11)

Отже зв’язок (3.6.8) з урахуванням знайденої функції (3.6.11) матиме такий вигляд:

(3.6.12)

Якщо відома початкова умова В = В₀ ,

коли t = 0, то з рівності (3.6.12) одержимо

Звідки находимо невідому сталу А₁

(3.6.13)

Враховуючи вираз (3.6.13), знаходимо із

загального розв'язку (3.6.12) шуканий розв'язок у такому

(3.6.14)

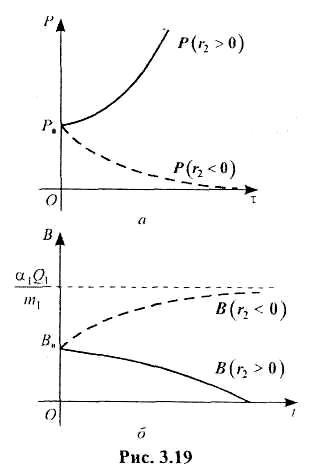
Отже, функції (3.6.4) і (3.6.14) є шуканим розв'язком системи рівнянь (3.6.2)—(3.6.3), описує динаміку двох видів популяції, між якими існують взаємовідносини типу «хижак- жертва». На рис. 3.19 зображено графіки функцій Р і В, що є розв'язком системи (3.6.2)-(3.6.3) для різних співвідношень параметрів r₂ , т₁, т₂ Якщо друга популяція («хижак»), як і перша, одержує сталий запас кормів, то відповідна математична модель описуватиметься такою системою диференціальних рівнянь:

(3.6.15)

(3.6.16)

де α₁,α₂ - коефіцієнти засвоєння їжі,

т₁ т₂,- коефіцієнти смертності, γ - коефіцієнт поїдання (пригнічення).

Проводячи викладки, аналогічні попередньому випадку, одержимо розв'язок цієї системи в такому вигляді:

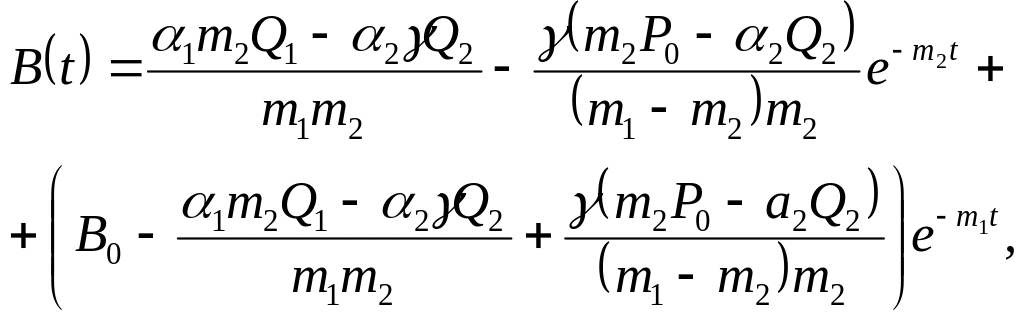(3.6.17)

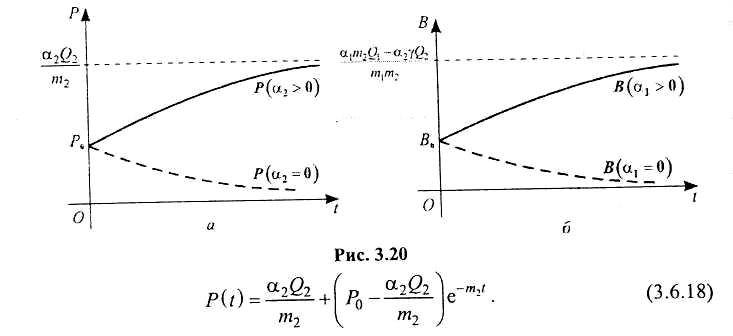
Якщо припустимо, що α₁=α₂ =0 (закрита екосистема), то система рівнянь (3.6.15)—(3.6.16) набуде такого вигляду:

(3.6.19)

(3.6.20)

А її розв’язок одержимо з розв’язку (3.6.17), (3.6.18) в такому вигляді:

(3.6.21)

(3.6.22)

де В_о, Р_о - початкова кількість тварин (організмів) одного і другого видів

На рис. 3.20 зображено графіки функцій В(t) і Р(t) для різних співвід­ношень параметрів α₁, α₂ , т₁, т₂, що входять у розв'язок системи (3.6.15), (3.6.16).

3.6.3. Структура трофічної функції

В. Вольтерра розглянув систему рівнянь, що описує взаємодію жертви з чисельністю (або біомасою) X і хижака з чисельністю Y в такому вигляді

(3.6.23)

(3.6.24)

В разі відсутності хижака (Y = 0) зростання чисельності (або щільності) жертви відбувається за логістичним рівнянням з питомою швидкістю розмноження а і ємністю середовища . Член (-bХ² ) описує дію пригнічення розвитку популяції за рахунок внутрішньої конкуренції. Цей член часто називають демпфіруючим, тобто таким, що зменшує амплітуду коливання, як це спостерігається в техніці. Через b і е позначено коефіцієнти смертності, а параметри с і d називають трофічними коефіцієнтами (або функціями).

Останнім часом для моделювання системи «хижак жертва» або «споживач - ресурс» широко застосовується така система рівнянь:

(3.6.25)

(3.6.26)

де R - кількість ресурсу, N- кількість (біомаса) особин популяції споживачів,

Q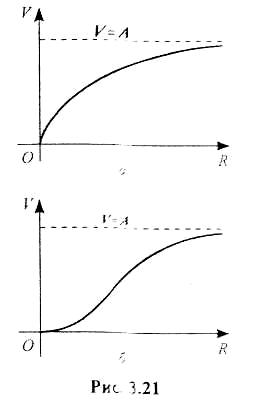 - швидкість надходження ресурсу в систему, V(R,N) -трофічна функція, яка моделює швидкість споживання ресурсу однією особиною популяції (питома швидкість споживання), к < 1 - частина ресурсу, шо використову­ється на продуктивні цілі, т - коефіцієнт смертності, який обернено пропорціональний середній тривалості життя особин в певних умовах навколиш­нього середовища. Найпростіша ситуація, коли величини Q, k і т сталі.

Відносно вибору трофічної функції V(R,N)

зустрічаються різні міркування, окремі з яких

були розглянуті в попередніх випадках.

Приймають також, що трофічна функція залежить

тільки від R, причому в нулі вона дорівнює нулю,

а при збільшенні R вона зростає і асимптотично

прямує до величини V = А (рис. 3.21).

Останнє обмеження відображає той факт,

шо навіть за великої кількості ресурсу

швидкість його споживання завжди обмежена.

Як свідчать результати багатьох реальних

спостережень, усю різноманітність трофічних

функцій можна розділити в основному на два великих класи

(типи): до першого належать обмежені функції з

опуклим догори графіком (рис. 3.21. а), а

до другого класу - обмежені функції з

сигмоподібним графіком (рис. 3.21, б).

Перший клас трофічних функцій характерний для безхребетних хижаків і багатьох видів хижих риб. другий клас - для популяцій та організмів з досить складною поведінкою і здатних до навчання. Такою поведінкою відрізняються хребетні хижаки, яких умовно можна назвати «розумними» [1].

Додаток . Зразки складання простих програм на Borland Pascal.

Приклад Д1.

Необхідно за введеним із клавіатури значенням температури за шкалою Цельсія визначити відповідне значення температури за шкалою Кельвіна. Обчислення виконуються за простою формулою:

proqram EX_1; Лістінг програмного коду