Var I,j,k: Integer;
y,w: Real;
BEGIN
FOR i:=1 TO n DO
{приведення матрицi системи (1) до трикутного виду (3)}
BEGIN
k:= i; y := a[i,i];
FOR j:= i+1 TO n DO
BEGIN w := a [j,i];
IF Abs (w) > Abs(y) THEN BEGIN k := j; y := w END
END;
IF Abs (y) <e THEN BEGIN Write ('НЕ ВИЗНАЧЕНО'); goto 1 END;
FOR j := i TO n+1 DO
BEGIN w := a[k,j]; a[k,j]:= a [i,j]; a[i,j] := w/y END;
FOR k := i+1 TO n DO
FOR j :=n+1 DOWNTO i+1 DO a[k,j] := a[k,j]-a[i,j]*a[k,i]
END;
FOR i := n DOWNTO 1 DO {Зворотний хід метода Гаусса}
BEGIN w := 0;
FOR j := i+1 TO n DO w := w+a[i,j]*x[j];
x[i] := a[i,n+1]-w
END;
1:
END{ linequ };
Var I, j : Integer;
u : Real;
c : ar1;
BEGIN
{ обчислення елементiв розширеної матрицi С у (13);}
FOR i := 0 TO n DO a [i] :=1;
FOR i := 0 TO 2*m DO
BEGIN
u := 0;
FOR j := 0 TO n DO u := u+a[j];
IF i<=m THEN
BEGIN
FOR j := 0 TO i DO c[i-j+1,j+1] := u;
u := 0;
FOR j := 0 TO n DO u := u+y[j]*a[j];
C[i+1,m+2] := u
END
ELSE IF i<>2*m THEN FOR j := i MOD m TO m DO c[i-j+1,j+1]:=u
ELSE c[m+1,m+1] := u;
FOR j := 0 TO n DO a[j] := a[j]*x[j]
END;
{ розв'язування системи (13) програма (Д3);}
Linequ(c,m+1,1E-6,a);
t := 0;
FOR i := 0 TO m DO a[i] := a[i+1];
FOR i := 0 TO n DO
BEGIN
U := 0;
FOR j := m DOWNTO 1 DO u := (u+a[j])*x[i];
{обчислення середньоквадратичної похибки за формулою (14).}
t := t+Sqr(y[i]-u-a[0])
END;
t := Sqrt(t/(n+1))
END;
BEGIN{Операторна частина контрольного приклада.}
m:=4;
n:=5;
for i:=0 to 5 do x[i]:=i;
y[0]:=2; y[1]:=3;y[2]:=7;y[3]:=10;y[4]:=18;y[5]:=26;
apr(m,n,x,y,t,a);
for i:=0 to 5 do
writeln(' Вiдповiдь a',i:1,'=',a[i]:2:6);
writeln(' Похибка t=',t:0:6);
writeln('Press Enter');
readln;
END.
Завдання для самостійної роботи:
Скласти блок-схему програм Д3 і Д4 і модернізувати алгорим для вводу початкової інформації з файлів.
Додаток 2 .Зразки тестових питань для самоперевірки:
К розділу 1.
11. Математичне моделювання – це моделювання,
1)що засновано на подібності процесів і явищ, що мають різну фізичну природу, але однаково описуються формально (одними й тими ж математичними рівняннями і т.п.);
2)що основане не на матеріальній аналогії об’єкта і моделі, а на аналогії уявній;
3)основане на інтуїтивному уявленні про об’єкт дослідження, що не піддається формалізації чи не має в ній потреби; 4)при якому реальному об’єкту протипоставляється його збільшена чи зменшена копія..
5)при якому дослідження об’єкта здійснюється через модель, сформульовану з використанням тих чи інших математичних методів.
12. Моделі із зосередженими значеннями (параметрами) описують …
1) відтворення будь-якого явища всесвіту за допомогою його матеріальної копії;
2) такі характеристики (параметри) природної системи, які не залежать від часу.
3)процес побудови моделі;
4)такі характеристики (параметри) природної системи, які залежать від часу і координати простору;
5)такі характеристики (параметри) природної системи, які залежать тільки від часу.
К розділу 2.
21. Періодична функциональна залежність Y=f(X) може мати вигляд:
1. Y = K*X + B; 2. Y =K/X; 3. Y = N0Xn ; 4. Y=Sin(X); 5.Y=X*X.
22. Рівняння Міхаеліса-Ментен для швидкості V поїдання субстрату S мікроорганізмами має вигляд:
1. V = 0.5*Vmax; 2. V = K/S; 3. V = N0Sn ; 4. V=Sin(S); 5.V=Vmax*S/(Km+S).
23. Графік рівняння Міхаеліса-Ментен для швидкості V поїдання субстрату S мікроорганізмами є:
1)парабола; 2)гіпербола; 3)пряма лінія; 4)коло; 5)періодична функція.
К розділу 3.
31. Закон швидкості розмноження популяції без обмежень має вигляд:
1).
;
2)
;
3)
;
4)
5)
32. Динаміка взаємовідносин типу «хижак-жертва» двох видів популяцій опишеться такою системою 2 –х диференціальних рівнянь:
1)
2)
3)
4)
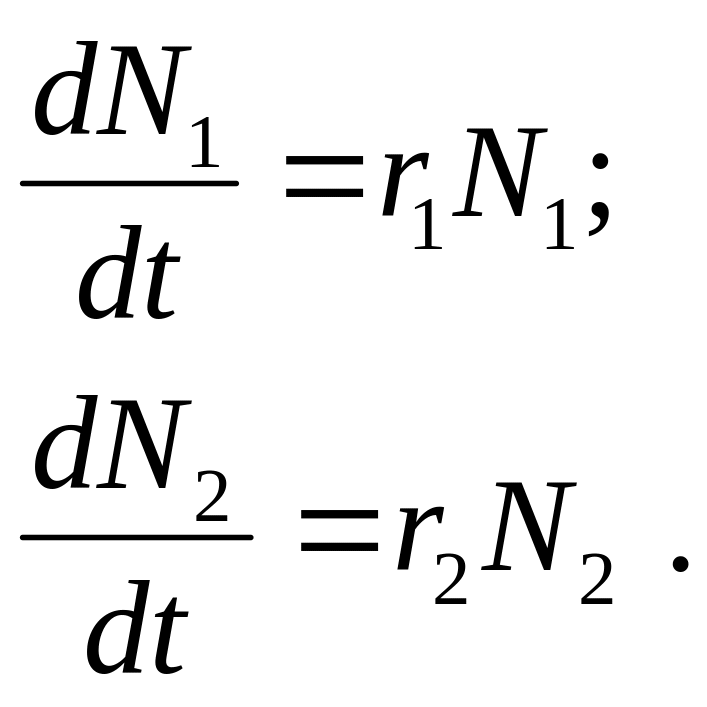
К додатку.
41. Перевірити синтаксис програмного коду програми ПОПУЛЯЦІЯ. Відповідь записати як порядковий номер строки, що містить помилку.
1) Program Populiacija2;
2) var P0, P1, P2, P, r : real; t : integer; const t1 = 10; t2 = 11; N = 100;
3) begin P0 := 10*N; P1 := 100N + 15; r := (ln(P2) – ln(P1))/(t2 – t1);
4) for t := 1 to 9 do begin P := P0 * exp(r*t);
5) writeln (t:4, ‘ | ‘, P:6:2) end;
6) readln; end.
Література
Лаврик В. І. Методи математичного моделювання в екології: Навч. посібник. – К.: Видавничий дім «КМ Академія», 2002. ‑ 202 с.
Ковальчук П. І. Моделювання і прогнозування стану навколишнього середовища: Навч. посібник. – К.: Либідь, 2003. – 208 с.
Кучерявий В. П. Екологія. – Львів: Світ, 2001. – 499 с.
Білявський Г.О., Падун М.М., Фурдуй Р.С. Основи загальної екології. – К.: Либідь, 1995. – 308 с.
Білявський Г.О., Бутченко Л.І. Основи екології: теорія та практикум. – К.: Лібра, 2004. – 368 с.
Жалдак М. I., Рамській Ю. С. Чисельні методи математики. – К.: Радянська школа, 1984. – 208 с.
Ковалюк Т. В. Основи програмування. – К.: Видавнича група BHV, 2005. – 384 с.
Гринчишин Я.Т. Turbo Pascal.Чисельні методи в фізиці та математиці. Тернопіль, 1994.-121 с.
Диханов Сергій Михайлович
МАТЕМАТИЧНЕ ТА
КОМП’ЮТЕРНЕ
МОДЕЛЮВАННЯ В ЕКОЛОГІЇ