3.3. Загальні принципи моделювання екологічних процесів за допомогою диференціальних рівнянь, стаціонарні розв'язки та їх стійкість

Як було зазначено у розділі 1.4, при побудові математичної моделі реальної екологічної системи вводяться певні математичні символи, які позначають змінні й постійні величини, що характеризують кількісні властивості даної системи. Як правило, змінні величини є скалярні функції часу і описують чисельність, біомасу або густоту досліджуваної популяції, біоценозу і т. ін.

Математична модель вважається побудованою, якщо знайдено функції , що визначають характер зміни в часі (динаміку) основних компонентів екосистеми, які позначимо через с₁(t),с₂(t),с₃(t), ..., с_n(t),залежно від зміни параметрів зовнішнього середовища. Невідомі функції с₁ =F₁ (t), с₂ =F₂ (t), c₃ =F₃(t), ..., с_n=Р_n{t) знаходяться з деякого співвідношення яким найчастіше виступає одне або кілька (система) диференціальних рівнянь, де невідома функція входить під знак похідної. Найпростіші моделі такого типу були розглянуті в розділі 3.1.

3.3.1. Загальний вигляд математичної моделі

В загальному випадку математична модель, що побудована;за/ допомогою звичайних диференціальних рівнянь, має такий вигляд:

(3.3.1)

де с₁ (t),с₂(t),с₃(t),..,с_n(t) - невідомі функції часу, що описують показники (характеристики) компонентів екологічної системи; - швидкості зміни показників екосистеми (концентрації речовини, чисельності або біо­маси організмів); f_j - функції, які залежать від зовнішніх і внутрішніх параметрів екосистеми (j = 1, 2, 3, ..., n).

Функції можуть бути як лінійні, так і нелінійні. Якщо функції не залежать явно від часу t, то система рівнянь (модель) називається автоном­ною (динамічною або консервативною) і записується таким чином:

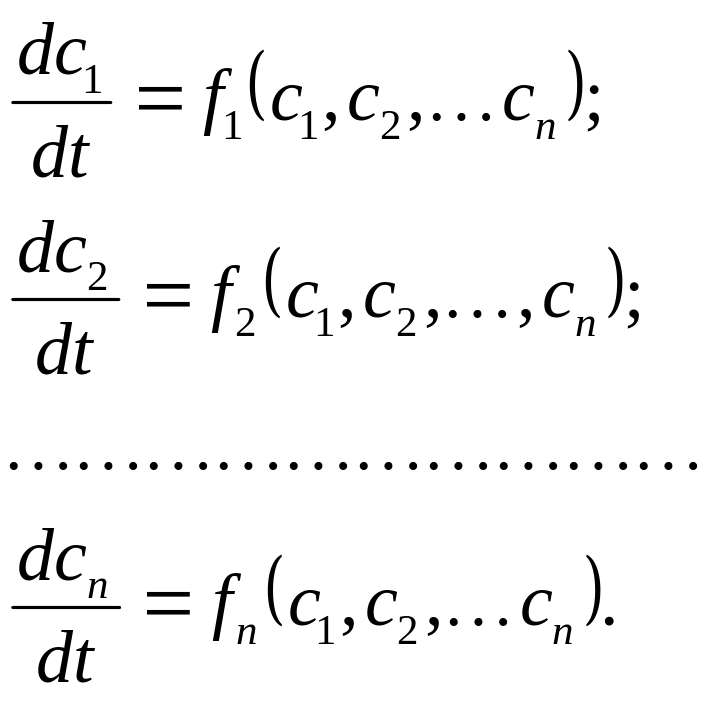(3.3.2)

Якщо права частина системи (3.3.1) є лінійні функції, то відповідна система рівнянь називається лінійною і записується у такому вигляді:

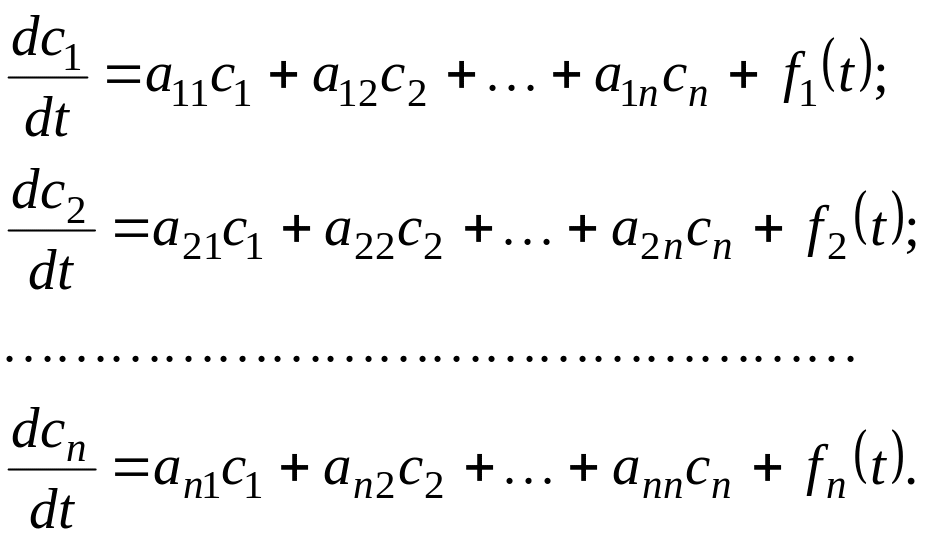(3.3.3)

Лінійні диференціальні рівняння не завжди можуть детально описати складні екологічні процеси, що потребують глибокого дослідження та аналізу. Але в багатьох випадках доцільність їх використання для вивчен­ня екологічних систем і процесів не викликає жодних сумнівів, тим паче, що методи розв'язування диференціальних лінійних рівнянь розвинуті значно краще, ніж методи розв'язування нелінійних рівнянь.

Якщо виникає необхідність моделювання поведінки (стану) екосистеми або її окремих компонент при змінних у часі зовнішніх умовах (наприклад, таких, що змінюються періодично або випадково), то задача зво­диться до розгляду неавтономної системи (3.3.1) або (3.3.3). При цьому спочатку будується і досліджується автономна система (модель), потім, залежно від характеру змінних зовнішніх умов, або до правої частини рівнянь (3.3.2) додаються нові члени, що залежать явно від часу, або постійні коефіцієнти замінюються змінними, що залежать від часу.

Як уже зазначалось, задача моделювання полягає в тому, щоб розв'язати систему диференціальних рівнянь (3.3.1), (3.3.2) або (3.3.3), тобто знайти невідомі функції:

(3.3.4)

які б задовольняли відповідні диференціальні рівняння і додаткові (початкові) умови:

(3.3.5)

Функції (3.3.4) називаються розв’язками або інтегралами диференціальних рівнянь, а їх графіки, побудовані в (n + 1) просторі, називаються інтегральними кривими.

В загальному випадку знайти аналітичні розв'язки нелінійних систем (3.3.1) або (3.3.2) можна далеко не завжди. Але наближені (чисельні) розв'язки можна знайти майже завжди за допомогою сучасних чисельних методів й електронних обчислювальних машин (ЕОМ). Разом з тим, не завжди доціль­но знаходити точний або наближений розв'язок, можна обмежитись якісним аналізом шуканих розв'язків і з'ясувати найбільш цікаві властивості динаміки системи, зокрема умови її рівноваги і стійкості. Для цієї мети існує спеціальна якісна теорія диференціальних рівнянь, на якій ми детально у даному курсі зупинятися не будемо, а розглянемо тільки її основні поняття, які будуть корисними при побудові простих математичних моделей.

Основний підхід в якісній теорії диференціальних рівнянь полягає в тому, що стан динамічної системи (екосистеми) характеризується змінними с₁, с₂, с₃, …,с_т, які в кожен момент часу набувають певних значень відповідно до системи (3.3.2). Якщо в n-мірному просторі відкласти на осях координат значення змінних с₁, с₂, с₃,..., с_п,, то стан системи буде характеризуватися точкою М(c₁,с₂,с_3,...,с_n), яка в просторі буде описувати деяку криву. Цю криву називають фазовою траєкторією системи (3.3.2), а простір, в якому проходить ця крива, - фазовим простором автономної системи (3.3.2).

Будь-яка фазова траєкторія належить до одного з трьох типів:

1. гладка крива без точок самоперетину;

2. замкнута крива (цикл), що описує періодичний процес;

3. точка, що відповідає положенню рівноваги системи.

Якісна теорія диференціальних рівнянь дозволяє описувати поведінку фазових траєкторій і цим самим досліджувати реальні системи (екосистеми). Сукупність фазових траєкторій, що відповідають різним початковим умовам, називається фазовим портретом системи (3.3.2).

Звичайно, фазові траєкторії несуть менше інформації про досліджува­ну систему, ніж інтегральні криві, які дають повну інформацію. Проте, в багатьох випадках досить знати поведінку (структуру) фазових траєкто­рій. Зауважимо, що фазова траєкторія для одного диференціального рівняння являє собою пряму, яка називається фазовою прямою.

Одна з важливих властивостей автономної системи (3.3.2) полягає в тому, що вона може мати стаціонарні розв’язки, які визначають стан рівноваги реальної системи або процесу. У положенні рівноваги всі показники екосистеми ( ) не змінюються в часі, тобто не залежать від часу. Тому в стаціонарному положенні всі похідні за часом у системі (3.3.2) дорівнюють нулю. Отже, прирівнявши до нуля праві частини рівнянь (3.3.2), одержимо систему алгебраїчних рівнянь для визначення стаціонарних зна­чень ,а саме:

Точка фазового простору М* ( )називається стаціонарною, або особливою, точкою, або точкою рівноваги системи.

3.3.2 Стійкість стаціонарних розв'язків

Після знаходження стаціонарних розв'язків автономної систе­ми (3.3.2) виникає питання про їх стійкість, а отже, і про стійкість рівноважної реальної системи.

С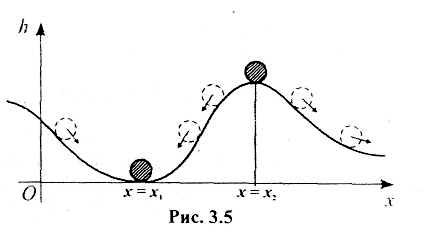 тійкий стан рівноваги можна визначити таким чином: якщо при досить малому початковому відхиленні від положення рівноваги система (розв'язок) ніколи не відхиляється далеко від цього положення, то стан рівноваги є стійким і відповідає стійкому стаціонарному режиму функціонування реальної системи. Якщо ж система після виведення її зі стану рівноваги з часом відхилятиметься від цього стану відповідно до рівняння (3.3.2), то такий стан рівноваги є нестійким.

Поняття стійкості легко пояснити на прикладі механічної стійкості. Розглянемо металеву кульку, що котиться по хвилястій поверхні (рис. 3.5). Для такої кульки є два положення рівноваги: одне - коли вона знаходиться в найнижчій точці поверхні (на дні впадини х = х₁), друге - коли кулька знаходиться в найвищій точці поверхні (наприклад, на вершині гірки х = х₂). Зрозуміло, що перше положення рівноваги кульки є стійким (невеликі відхилення кульки приведуть до затухаючих коливань навколо положення рівноваги), а друге положення є нестійким (невеликі відхилення кульки від цього положення призведуть до великого зміщення кульки і вона займе або перше положення, або віддалятиметься на нескінченність).

Значний інтерес являє собою дослідження стійкості екологічних систем, які теж можуть мати як стійкі, так і нестійкі положення рівноваги. Нестійкі положення рівноваги з часом можуть переходити у стійкі або система набуде нереальних (критичних) форм, або, нарешті, може загинути. Всі ці випадки описуються точковими математичними моделями, що побудовані за допомогою звичайних диференціальних рівнянь та їх систем.

У разі, коли моделююча система описується одним диференціальним рівнянням виду

(3.3.7)

питання про стійкість положення рівноваги системи можна розв'язати, досліджуючи поведінку функції (c), тобто характер зміни похідної За означенням стаціонарній точці с = с^* похідна дорівнює нулю:

(3.3.8)

Розглянемо, як змінюються розв'язки (інтегральні криві) в околі точки с = с* залежно від значень похідної (c_n), при с_п < с^* і при с_п > с^*. Побудуємо також фазові прямі.

Існує три варіанти.

1 . Нехай відомо, що в околі положення рівноваги с* похідна (с) змінює знак з «+» на «-» при зростанні с. Отже, при с_п < с* маємо , а це означає, що всі значення с_п, розміщені нижче від прямої с = с*, збільшуються, тобто прямують до с*. При с_п > с* маємо , а це означає, що всі значення c_n, розміщені вище від прямої с = с*, зменшуються, тобто теж прямують до с^* (рис. 3.6). Отже, всі інтегральні криві, що знаходяться на деякій віддалі від положення рівноваги, прямують до нього при зростанні часу t. Очевидно, що ми маємо ситуацію, коли положення рівноваги є стійким.

2. Тепер розглянемо варіант, коли в околі положення рівноваги с* похідна (с) міняє знак «-» на «+» при зростанні змінної с. Тоді при с_п < с*

маємо , а це означає, що всі значення с_п, розміщені нижче прямої с = с*, зменшуються, тобто відділяються від положення рівноваги с = с^*.

При с_п > с маємо , а це означає, що всі значення с_n, розміщені вище від прямої с = с*, збільшуються, тобто теж віддаляються від положення рівноваги с = с* (рис. 3.7) У даному разі, як бачимо, положення рівноваги нестійке.

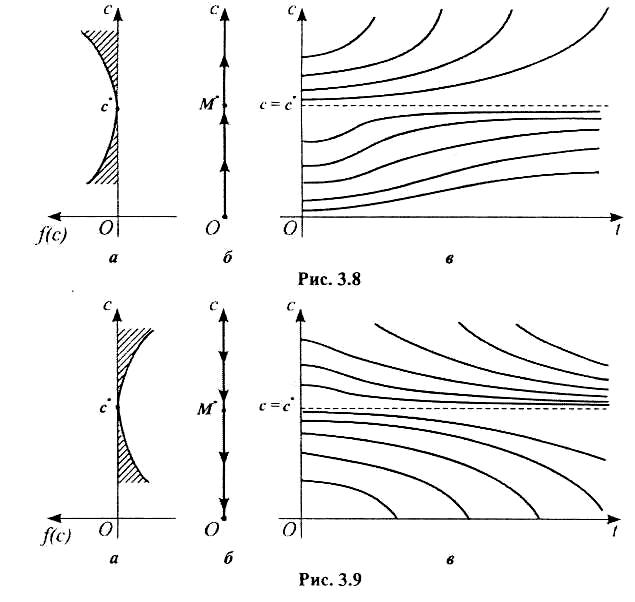
3. Якщо в околі точки с* похідна (с) не змінює знак, то за такої ситуації з одного боку від положення рівноваги с = с* значення с_п набли­жаються до с*, а з іншого боку від прямої с = с* значення с_п віддаляються від с* (рис. 3.8 і 3.9). Отже, положення рівноваги буде теж нестійким.

Для дослідження стійкості положення рівноваги системи з двох і біль­ше диференціальних рівнянь відомим математиком О. М. Ляпуновим (1857-1918) розроблений спеціальний метод [11, 12, 106, 138, 139, 141].

Динамічні системи, що описуються системами звичайних диференці­альних рівнянь типу (3.3.1), (3.3.2) або (3.3.3), називаються точковими системами, або точковими моделями. Це означає, що в усіх точках простору для такої системи значення концентрації однієї і тієї ж речовини (або щільності популяції) рівні в кожен момент часу.

Більш загальними є моделі, що описують зміну концентрації речовини не тільки в часі, а й у просторі, коли на розподіл речовин впливають дифузійні або інші процеси.