2. Интегрирование иррациональных функций.

Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.

Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.

1. Интеграл вида 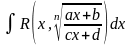где n- натуральное число.

С помощью подстановки функция рационализируется:

Тогда

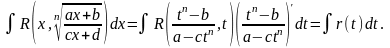
Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.

2. Интеграл вида , где R-рациональная функция своих аргументов.

Пусть R-общий знаменатель дробей m/n,…r/s.Сделаем подстановку .Тогда каждая дробная степень х выразится через целую степень t и, следовательно, подынтегральная функция преобразуется в рациональную функцию от t.

3. Решить систему методом Крамера.

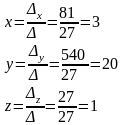
Проверка:

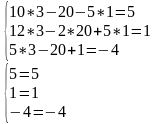
4. Исследовать функцию на непрерывность и сделать чертёж её графика.

Точка х=-2 – точка разрыва функции.

Р азрыв второго рода.

у

2

-2 0 х

БИЛЕТ № 9.

1. Линейно зависимые и линейно независимые системы векторов в пространстве r2 и r3.

Система векторов 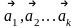называется линейно зависимой, если существуют числа , не равные нулю одновременно, такие, что .

Если последнее равенство выполняется только при , система векторов называется линейно независимой.

В пространстве Rⁿ любая система, содержащая более чем n векторов, линейно зависима.

Линейную зависимость системы векторов из Rⁿ можно установить следующим образом. Сравнивая координаты векторов из левой и правой части векторного равенства , получим однородную систему уравнений. Система векторов линейно зависима тогда и только тогда, когда получившаяся однородная система линейных уравнений имеет ненулевое решение.

2. Взаимное расположение прямой и плоскости в пространстве.

Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке.

Теорема. Пусть плоскость  задана общим уравнением , а прямая L задана каноническими уравнениями или параметрическими уравнениями

, , в которых  – координаты нормального вектора плоскости ,  – координаты произвольной фиксированной точки прямой L,    –

координаты направляющего вектора прямой L. Тогда:

1) если , то прямая L пересекает плоскость  в точке, координаты которой  можно найти из системы уравнений            

;

2) если  и , то прямая лежит на плоскости;

3) если  и , то прямая параллельна плоскости.

Доказательство. Условие  говорит о том, что вектроры  и  не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит пересекает ее в некоторой точке М. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе уравнений. Решаем первое уравнение системы относительно неизвестной t и затем, подставляя найденное значение t в остальные уравнения системы, находим координаты искомой точки.

Если , то это означает, что . А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости и координаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка . Если , то точка  – лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.

Если , а , то точка на прямой не лежит на плоскости, а это означает, что прямая параллельна плоскости.

Теорема доказана.