2. Вектор-функция. Выражение для кривизны в произвольных координатах.

Пусть каждому значению поставлен в соответствие вектор трехмерного пространства. В этом случае говорят, что на множестве D задана векторная функция.

Если в пространстве задана декартова система координат, то задание вектор-функции означает задание скалярных функций x (t), y (t), z (t). Если – единичные векторы координатных осей, то .

Множество точек, заданных радиус-векторм r(t) = x(t)i + y(t)j + z(t)k, t∈[a, b]  соответствующим непрерывной на отрезке [a, b]  вектор-функции r(t) называют непрерывной кривой, или просто кривой, а аргумент t - параметром кривой.

Первая производная векторфункции даёт нам простейшую характеристику линии y=f(x), а именно её направление. Вторая производная тесно связана с другой количественной характеристикой этой линии, с так называемой кривизной, устанавливающей меру изогнутости или искривлённости линии.

3. Найти , если 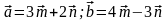и известны координаты векторов 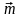и : и .

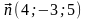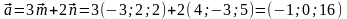
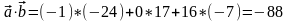
4. Найти точки разрыва функции и определить характер разрывов в этих точках.

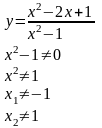
Точки разрыва функции.

Разрыв второго рода.

Устранимый разрыв.

БИЛЕТ № 7.

1. Теорема о пределе трёх функций.

Теорема 1. Если существуют пределы  

Теорема 2. ,

т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности, ;

                                                                 

Теорема 3.

2. Вектор-функция. Определение, предел, непрерывность и дифференцируемость.

Пусть каждому значению поставлен в соответствие вектор трехмерного пространства. В этом случае говорят, что на множестве D задана векторная функция.

Если в пространстве задана декартова система координат, то задание вектор-функции означает задание скалярных функций x (t), y (t), z (t). Если – единичные векторы координатных осей, то .

Если для любого t начало вектора совпадает с началом координат, то говорят о радиус-векторе.

Вектор называется пределом вектор-функции при если

Пусть    

Тогда

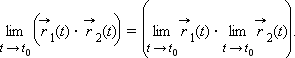
Вектор-функцию называют непрерывной в точке t₀, если

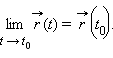
Дифференциалом вектор-функции  называют линейную вектор-функцию Производная вектор-функции в точке определяется аналогично производной функции одного переменного:

Аналогично вводится понятие второй производной и производных более высоких порядков. Производная вектор-функции связана с ее дифференциалом формулой:

или

3. Найти обратную матрицу к матрице и сделать проверку.

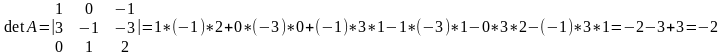
Проверка:

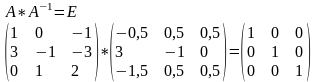
4. Вычислить .

БИЛЕТ № 8.

1. Необходимое условие существования точек локального экстремума функций.

Теорема (необходимое условие существования экстремума): если функция f(x) дифференцируема в точке х = х₁ и точка х₁ является точкой экстремума, то производная функции обращается в нуль в этой точке.

Доказательство. Предположим, что функция f(x) имеет в точке х = х₁ максимум. Тогда при достаточно малых положительных х>0 верно неравенство:

, т.е.

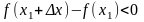
Тогда

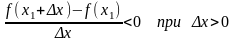
По определению:

Т.е. если х0, но х<0, то f(x₁)  0, а если х0, но х>0, то f(x₁)  0. Это возможно только в том случае, если при х0 f(x₁) = 0.

Для случая, если функция f(x) имеет в точке х₂ минимум теорема доказывается аналогично.

Теорема доказана.

Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х³, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум.