2. Интегрирование рациональных функций.
Для
интегрирования рациональной функции
,
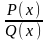где P(x)
и Q(x)
- полиномы, используется следующая
последовательность шагов:
Шаг 1. Преобразование неправильной рациональной дроби
Если дробь неправильная (т.е. степень числителя P(x) больше степени знаменателя Q(x)), разделим многочлен P(x) на Q(x). Получим следующее выражение:
где
- правильная рациональная дробь.
Шаг 2. Разложение знаменателя на простейшие дроби
Запишем многочлен знаменателя Q(x) в виде
где квадратичные функции являются несократимыми, то есть не имеющими действительных корней.
Шаг 3. Разложение рациональной дроби на сумму простейших дробей.
Запишем рациональную функцию в следующем виде:
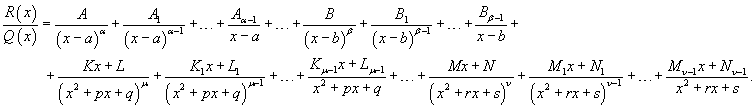
Общее число неопределенных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , ... должно быть равно степени знаменателя Q(x). Затем умножим обе части полученного уравнения на знаменатель Q(x) и приравняем коэффициенты при слагаемых с одинаковыми степенями x. В результате мы получим систему линейных уравнений относительно неизвестных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , .... Данная система всегда имеет единственное решение. Описанный алгоритм представляет собой метод неопределенных коэффициентов.
Шаг 4. Интегрирование простейших рациональных дробей.
Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул:
У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат:
где
Затем применяются следующие формулы:
Интеграл
может
быть вычислен за k
шагов с помощью формулы редукции
3. Найти угол между векторами и , если а (1;5;8), в (-3;7;2), с (6;4;-1), точка д является серединой отрезка ав.
Координаты точки Д:
4. Вычислить .
Применим правило Лопиталя
БИЛЕТ № 6.
1. Интегрирование тригонометрических функций.
1.
Интеграл вида
.
Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.
Интегралы
этого вида вычисляются с помощью
подстановки
.
Эта подстановка позволяет преобразовать
тригонометрическую функцию в рациональную.
,
Тогда
Таким
образом:
2. Интеграл вида если функция R является нечетной относительно cosx.
Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.
Функция
может содержать cosx
только в четных степенях, а, следовательно,
может быть преобразована в рациональную
функцию относительно sinx.
3. Интеграл вида если функция R является нечетной относительно sinx.
По аналогии с рассмотренным выше случаем делается подстановка t = cosx.
Тогда
Интеграл вида функция R четная относительно sinx и cosx.
Для преобразования функции R в рациональную используется подстановка
t = tgx.
Тогда
4. Интеграл произведения синусов и косинусов различных аргументов.
В зависимости от типа произведения применятся одна из трех формул:
