3. Найти косинус угла при вершине с в треугольнике авс, если известны координаты вершин треугольника: а (-1;0;4), в (0;-1;3) и с (1;0;4).

Угол АСВ – это угол между векторами и .

(-1-1;0-0;4-4) = (-2;0;0)

(0-1;-1-0;3-4) = (-1;-1;-1)

4. Вычислить интеграл .

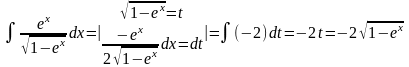
БИЛЕТ № 3.

1. Обратная матрица. Формула для нахождения обратной матрицы.

Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:

XA = AX = E,

где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А^-1.

Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну.

Общий подход к нахождению обратной матрицы.

Исходя из определения произведения матриц, можно записать:

AX = E  , i=(1,n), j=(1,n),

e_ij = 0, i  j,

e_ij = 1, i = j .

Таким образом, получаем систему уравнений:

,

Решив эту систему, находим элементы матрицы Х.

Но такой способ не удобен при нахождении обратных матриц больших порядков, поэтому обычно применяют следующую формулу:

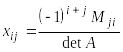
где М_ji – дополнительный минор элемента а_ji матрицы А.

2. Свойства неопределённого интеграла.

Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением: F(x) + C.

Записывают:

Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.

Свойства:

1.

2.

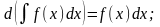
3.

4. где u, v, w – некоторые функции от х.

5.

3. Лежат ли точки А (-1;2;-1), В (0;-1;0) и Д (1;-8;7) на одной прямой? Ответ обосновать. Найти длину отрезка АД.

Составим уравнение прямой АД:

Проверим точку В:

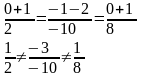
Значит точки А, В и Д не лежат на одной прямой.

Длина отрезка АД:

4. Вычислить интеграл

БИЛЕТ № 4.

1. Замена переменной и интегрирование по частям в неопределённом интеграле.

Замена переменной.

Если требуется найти интеграл , но сложно отыскать первообразную, то с помощью замены x = (t) и dx = (t)dt получается:

Интегрирование по частям.

Способ основан на известной формуле производной произведения:

(uv) = uv + vu

где u и v – некоторые функции от х.

В дифференциальной форме: d(uv) = udv + vdu

Проинтегрировав, получаем: , а в соответствии с приведенными выше свойствами неопределенного интеграла:

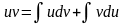или ;

Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.

2. Формулы Крамера.

Система из n уравнений с n неизвестными

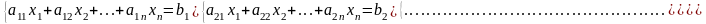
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:

x_i = _i/, где

 = det A, а _i – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i.

3. Записать каноническое уравнение плоскости, проходящей через точки А (1;-2;-3), В (0;-1;1) и С (-2;1;4). Лежит ли точка Д (0;-1;2) на этой плоскости? Ответ обосновать.

Уравнение плоскости, проходящей через 3 заданные точки:

Проверка точки Д:

Значит, точка Д лежит на плоскости.

4. Функция у от х задана неявно уравнением . Найти .

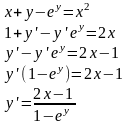
БИЛЕТ № 5.

1. Метод Гаусса.

Метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.

Рассмотрим систему линейных уравнений:

Разделим обе части 1–го уравнения на a₁₁  0, затем:

1) умножим на а₂₁ и вычтем из второго уравнения

2) умножим на а₃₁ и вычтем из третьего уравнения и т.д.

Получим:

,

где d_1j = a_1j/a₁₁, j = 2, 3, …, n+1.

d_ij = a_ij – a_i1d_1j i = 2, 3, … , n; j = 2, 3, … , n+1.

Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.