61. Исследование функций на экстремум при помощи производных высшего порядка.
Теорема. Пусть функция f ( x ) определена в некоторой ε – окрестности точки х0, причём f ' ( x0 ) = f '' ( x0) = … = f ( k - 1 ) = 0 и f (k) ( x0 ) ≠ 0. Тогда точка х0является точкой локального максимума, если k – чётное и f (k) ( x0 ) < 0, и точкой локального минимума, если k – чётное и f (k) ( x0 ) > 0. Если k – нечётное, то критическая точка х0 не является точкой экстремума; является точкой возрастания функции f ( x ) в случае f (k) ( x0 ) > 0 и является точкой убывания функции f ( x ) в случае f (k) ( x0 ) < 0. Доказательство. Воспользуемся формулой Тейлора для функции f ( x ) в точке х0:
.
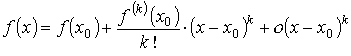Поэтому
.
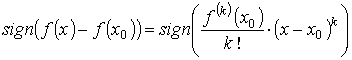Если k – чётное, то
sign ( f ( x ) − f ( x0 ) ) = sign ( f (k)( x0 ) ),
из чего следует вывод относительно экстремума функции в условиях этой теоремы. Если k – нечётное, то
sign (f ( x ) − f ( x0 )) = sign ( f (k)( x0 ) )·sign ( x − x0 ),
и приращение функции зависит от знака приращения аргумента с поправкой на знак величины f (k) ( x0 ), из чего следует вывод относительно точки монотонности функции в условиях этой теоремы.
62. Исследование функций на выпуклость и вогнутость. Точки перегиба функции.
Направление выпуклости вверх
Пусть функция у = f (x) дифференцируема на интервале (а, b). Тогда существует касательная к графику функции у = f (x) в любой точке М (х; f (x)) на интервале а <х < b, причем касательная не параллельна оси Оу, поскольку угловой коэффициент касательной, равный f ' (x), конечен. Определение. График функции y = f (x) имеет в данной точке х0 выпуклость, направленную вниз (вверх ), если в достаточно малой окрестности этой точки график функции расположен не ниже (не выше) касательной к графику функции, проведённой в этой точке. Аналитически это будет означать, что
f ( x ) ≥ f ( x0 ) + f ' ( x0 )·( x − x0 )
для выпуклости в данной точке вниз и
f ( x ) ≤ f ( x0 ) + f ' ( x0 )·( x − x0 )
для выпуклости в данной точке вверх. Будем говорить, что график функции y = f (x) имеет на выпуклость, направленную вниз (вверх) на интервале (а, b), если график функции выпуклый вниз (вверх) в любой точке этого интервала (а, b).
Связь направления выпуклости функции со знаком второй производной
Теорема. Для того, чтобы дважды дифференцируемая в точке x0 функция была выпукла вверх (вниз) в этой точке, необходимо и достаточно, чтобы вторая производная этой функции в x0 была неположительной (неотрицательной). Доказательство. Пусть функция y = f ( x ) выпукла вниз в точке х0. Разложим функцию в ряд Тейлора в данной точке х0:
.
Следует отметить, что первые два слагаемых ряда Тейлора совпадают с правой частью уравнения касательной, проведённой в графику функции y = f (x) в точке х0:
Y = f ( x0 ) + f '( x0 )·( x − x0 ).
Учитывая, что слагаемое o(x - x0)2 в достаточно малой окрестности точки х0 мало, и на знак выражения влияния не оказывает, получим зависимость знака второй производной на направление выпуклости
sign ( f ( x ) − Y) = sign ( f ''( x0 ) ).
Теорема. Для того чтобы дважды дифференцируемая на интервале (а, b) функция, была выпукла вверх (вниз) в нем, необходимо, чтобы во всех точках этого интервала вторая производная функции была ≤ 0 ( ≥ 0). Доказательство. Пусть функция в произвольной точке х0 Î (a, b) выпукла вниз. Тогда в достаточно малой окрестности точки х0 справедливо неравенство f ( x ) ≥ f ( x0 ) + f ' ( x0 )·( x - x0 ). Запишем последнее неравенство в виде
f ( x ) − f ( x0 ) − f ' ( x0 )·( x − x0 ) ≥ 0.
Применяя формулу Лагранжа к первому и второму слагаемому, получим
[ f ' ( c1 ) − f ' ( x0 ) ]·( x − x0 ) ≥ 0.
Применяя ещё раз формулу Лагранжа в квадратной скобке, получим
f '' ( c2 )·( c1 − x0 )·( x − x0 ) ≥ 0,
откуда непосредственно следует f '' ( c2 ) ≥ 0 так как x0 < с2 < c1 < x. Поскольку аргумент х выбран произвольно в достаточно малой окрестности точки х0, то и аргумент для второй производной в этом случае тоже произволен в достаточно малой окрестности точки х0.
Определение точки перегиба
Точка, в которой функция определена и в которой функция меняет направление выпуклости, называется точкой перегиба. В окрестности такой точки x 0 график функции y = f (x) слева и справа от точки x0 имеет разные направления выпуклости. Очевидно, что в точке перегиба касательная пересекает график функции так, что с одной стороны от этой точки график лежит под касательной, а с другой - над нею. В окрестности точки перегиба график функции геометрически переходит с одной сторон касательной на другую и "перегибается" через нее. Отсюда и произошло название "точка перегиба".
Необходимое условие точки перегиба
Теорема. Пусть функция y = f (x) дважды непрерывно дифференцируема на интервале (a, b). Для того, чтобы точка М(x0, f(x0)) была точкой перегиба графика функции y = f (x) необходимо, чтобы f " (x0) = 0. Доказательство. Предположим обратное, пусть f "(x0) ≠ 0. Тогда в силу непрерывности второй производной по теореме об устойчивости знака непрерывной функции существует окрестность точки x0, в которой f ″(x) < 0 (f "(x) > 0), и, значит график функции y = f (x) имеет определенное направление выпуклости в этой окрестности. Но это противоречит наличию перегиба в точке M(x0; f (x0 )). Полученное противоречие доказывает теорему. Не всякая точка М (x0, f (x0)), для которой f " (x0) = 0, является точкой перегиба. Например, график функции y = f(x) = x4 не имеет перегиба в точке (0; 0), хотя f " (х) = 12·x ² = 0 при х = 0. Поэтому равенство нулю второй производной является лишь необходимым условием перегиба. Точки М (x0; f (x0)) графика, для которых f"(x0) = 0, будем называть критическими. Необходимо дополнительно исследовать вопрос о наличии перегиба в каждой критической точке, для чего следует сформулировать достаточное условие перегиба.
Достаточное условие точки перегиба
Теорема. Пусть функция y = f (x) имеет вторую производную f "(x) в некоторой достаточно малой окрестности точки x0 интервала (a, b), за исключением, быть может самой точки х0, а график функции имеет касательную в точке С = (х0, f (x0)). Если при переходе через точку х0 вторая производная f "(x) меняет знак, то точка С является точкой перегиба графика функции y = f (x). Доказательство. Из того, что f "(x) слева и справа от точки x0 имеет разные знаки, то направление выпуклости графика функции слева и справа от точкиx0 является различным. Это и означает наличие перегиба в точке M(x0; f (x0)).