11 Модель равновесных цен . Рассмотрим теперь балансовую модель, двойственную к модели Леонтьева – так называемую модель равновесных цен. Пусть, как и прежде, А - матрица прямых затрат, (x_l, x₂,...,x_n) – вектор валового выпуска. Обозначим через (р₁, р₂, …р_n – вектор цен, i-я координата которого равна цене единицы продукции i-й отрасли; тогда, например, первая отрасль получит доход, равный p₁, х₁.

Часть своего дохода эта отрасль потратит на закупку продукции у других отраслей. Так, для выпуска единицы продукции ей необходима продукция первой отрасли в объеме a₁₁, второй отрасли в объеме а₂₁, n-й отрасли в объеме a_n1 т. д. На покупку этой продукции ею будет затрачена сумма, равная a₁₁ p₁ + a₂₁ p₂ +...+ a_nl p_n. Следовательно, для выпуска продукции в объеме х₁ первой отрасли необходимо потратить на закупку продукции других отраслей сумму равную x₁(a₁₁p₁ + a₂₁p₂ +...+ a_n1p_n). Оставшуюся часть дохода, называемую добавленной стоимостью, мы обозначим V₁ (эта часть дохода идет на выплату зарплаты и налогов, предпринимательскую прибыль и инвестиции).

Таким образом, имеет место следующее равенство:

x₁ p₁ = x₁ (a₁₁ p₁ +a₂₁ p₂ +… +a_n1 p_n) + V₁. Разделив это равенство на х₁ получаем p₁ = (a₁₁ p₁ +a₂₁ p₂ +… +a_n1 p_n) + v₁, где v₁ – норма добавленной стоимости (величина добавленной стоимости на единицу выпускаемой продукции). Подобным же образом получаем для остальных отраслей

p₂ = a₁₂ p₁ + a₂₂ p₂ + … + a_n2 p_n +v₂

……………………………………

p_n = a_1n p₁ + a_2n p₂ +…+ a_nn p_n +v₂

Найденные равенства могут быть записаны в матричной форме следующим образом: , где - вектор норм добавленной стоимости.

Как мы видим, полученные уравнения очень похожи на уравнения модели Леонтьева с той лишь разницей, что заменен на , – на , А – на А^т.

Модель равновесных цен позволяет, зная величины норм добавленной стоимости, прогнозировать цены на продукцию отраслей. Она также позволяет прогнозировать изменение цен и инфляцию, являющиеся следствием изменения цены в одной из отраслей.

12 ? Определение 10.1. Ненулевой вектор называется собственным вектором квадратной матрицы А порядка n, если где – некоторое число. При этом число называется собственным значением матрицы А. Говорят так: есть собственный вектор матрицы А, принадлежащий ее собственному значению .

13 Определение Уравнение называется характеристическим уравнением матрицы А. Таким образом, собственные значения матрицы А являются корнями ее характеристического уравнения.

14 Определение. Максимальное по модулю собственное значение неотрицательной матрицы А называется числом Фробениуса матрицы А, а соответствующий ему неотрицательный собственный вектор - вектором Фробениуса для А.

15 Определение. Функцию, выражающую зависимость между стоимостью выпускаемой продукции и стоимостью суммарных затрат на ее производство, называют однофакторной производственной функцией.

16 Функция, в которой роль независимой переменной играют затраты, а зависимая переменна определяет уровень выпуска, называется функцией выпуска. В функции затрат, наоборот, независимая переменная- выпуск, а зависимая- затраты.

Пример 1. Если затраты прямо пропорциональны объему выпуска , то функция затрат имеет вид .

С помощью однофакторных производственных функций описывается также зависимость объема выпускаемой продукции от затрат некоторого специфического вида ресурса (трудовые ресурсы, основные производственные фонды, объем капиталовложений, различные виды сырья и др.). При этом затраты всех других участвующих в производстве ресурсов считаются постоянными.

Пример 2. С помощью функции вида

можно охарактеризовать зависимость урожайности некоторой сельскохозяйственной культуры от количества внесенных удобрений. При отсутствии удобрений урожайность составляет единиц. С увеличением объема используемых удобрений урожай сначала возрастает и при достигает наибольшего значения.

Дальнейшее наращивание затрат удобрений оказывается неразумным, так как приводит к снижению урожая и даже полной его потере при (рис.1).

Пример 3. Гиперболическая зависимость

применяется, например, для моделирования зависимости затрат на единицу выпускаемой продукции от объема производства (рис.2). Величина уменьшается с увеличением , это означает, что с увеличением объема производства доля затрат неограниченно убывает. При большом объеме производства ( ) удельные затраты лишь незначительно отличаются от ( ).

Пример 4. Экспоненциальная производственная функция

используется, например, для исследования динамики изменения объема производств с течением времени . В начальный момент времени объем производства . Крутизна кривой зависит от коэффициентов . Зависимость имеет место ив следующей ситуации. Если на банковский счет кладется сумма , то через лет на счете будет сумма , если банк выплачивает % годовых.

Пример 5. Показательная функция

может моделировать влияние затрат переменного ресурса на выпуск продукции, если уровень выпуска не может быть больше некоторой предельной величины . Так как , то с ростом неограниченно убывает, а возрастает. Если , то . При выпуск равен

Пример 6. Степенная производственная функция

обычно описывает ситуации, в которых рост затрат некоторого ресурса ведет к неограниченному увеличению выпуска . Насколько быстро растет зависит от величины параметров .

17 Экономический смысл производной. Пусть функция выражает количество произведенной продукции за время . Необходимо найти производительность труда в момент времени .

За период времени от до количество произведенной продукции изменится от значения до значения . Тогда средняя производительность труда за этот период времени равна . Очевидно, что производительность труда в момент времени можно определить как предельное значение средней производительности за период времени от до при , т.е. равна .

Экономический смысл производной: производительность труда есть производная объема произведенной продукции по времени.

Производная логарифмической функции называется логарифмической производной, а так же относительной скоростью изменения функции или темпом изменения функции.

Пример 7. Объем продукции , произведенной бригадой рабочих, может быть описан уравнением , , где - рабочее время в часах. Вычислить производительность труда, скорость и темп ее изменения через час после начала работы и за час до ее окончания.

Производительность труда выражается производной , а скорость и темп изменения производительности – соответственно производной и логарифмической производной

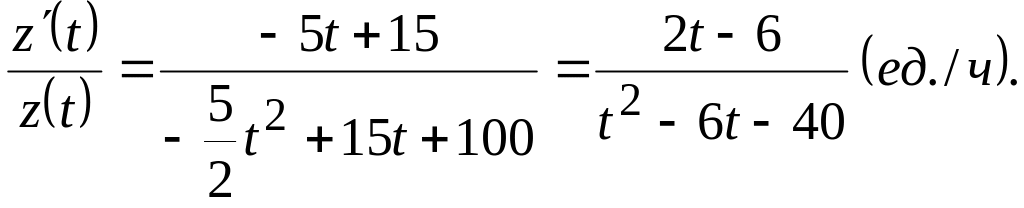
В заданные моменты времени соответственно имеем:

Итак, к концу работы производительность труда существенно снижается; при этом изменение знака и логарифмической производной с плюса на минус свидетельствует о том, что увеличение производительности труда в первые часы рабочего дня сменяется её снижением в последние часы.

18 Теорема Ферма. Если дифференцируемая на промежутке функция достигает наибольшего или наименьшего значения во внутренней точке этого промежутка, то производная функции в этой точке равна нулю, т.е. Один из базовых законов теории производства звучит так: оптимальный для производства уровень пуска товара определяется равенством предельных издержек и предельного дохода.

Обозначим функцию прибыли за . Тогда , где - функция дохода, - функция издержек. Очевидно, что оптимальным уровнем производства является тот, при котором прибыль максимальна, т.е. такое значение выпуска , при котором функция имеет экстремум (максимум). По теореме Ферма в этой точке . Но , поэтому , т.е. предельные издержки и предельный доход равны при оптимальном выпуске .

19 Теорема Лагранжа. Если функция непрерывна на промежутке и дифференцируема в , то существует по крайней мере одна точка , такая, что справедливо неравенство: .

Экономический смысл теоремы Лагранжа. Пусть описывает зависимость выпуска от затрат некоторого специфического ресурса. Если объем затрат увеличили с до единиц, то разность выражает соответствующее изменение выпуска.

20 Закон убывающей доходности: с увеличением производства дополнительная продукция, полученная на каждую новую единицу ресурса (трудового, технологического и т.Д.), с некоторого момента убывает.

Закон убывающей полезности: с ростом количества товара дополнительная полезность от каждой новой его единицы с некоторого момента убывает.