23. Общее уравнение плоскости. Нормальный вектор плоскости.
Пусть
Т
огда
n
– нормальный вектор плоскости α. n
и А полностью определяют плоскость α.
АХ и n – перпендикулярны.
AX*n=0
n={n1; n2; n3} – нормальный вектор.
Это уравнение плоскости, через точку А и перпендикулярный вектор n.
-- общее уравнение плоскости
-- нормальный вектор.
Прим.:
А(2; 1; -2)
n={-2; 4; 3}
AX*n=0
{
x-2;
y-1;
z+1}*{-2;
4; 3}=0
-2(x-2)+4(y-1)+3(z+1)=0
-2x+4y=3z+3=0 – общее уравнение плоскости.
Уравнения координатных плоскостей:
z=0 – уравнение плоскости (x; y)
x=0 – уравнение плоскости (y; z)
y=0 – уравнение плоскости (x; z)
24. Нормальное уравнение плоскости. Расстояние и отклонение точки от плоскости.
-
-
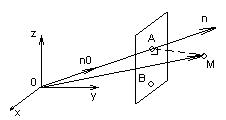
общее уравнение плоскости.
0 (0; 0;0) – начало координат.
А(а1; а2; а3) лежит в плоскости.
n – нормаль к плоскости
n0={cosα; cosβ; cosγ} – единичный вектор
M (x; y; z) – произвольная точка
В – проекция М на плоскость
d=|BM|=ρ(M; α)
p=|0A|= ρ(0; α)
0A=p*n0.
Отклонение σ точки М от плоскости α определяется по формуле:
σ(M; α)=ПрnAM
σ(M; α)=AM*n0
Пусть α не проходит через 0. Из определения отклонения видно, что:
σ(0; α)=-р
В этом случае начало координат имеет отрицательное отклонение.
σ=ОМ*n0-p=xcosα+ycosβ+zcosγ-p
Если М лежит в плоскости α, то σ = 0.
xcosα+ycosβ+zcosγ-p=0 – нормальное (нормированное) уравнение плоскости.
Как из общего уравнения плоскости получить отклонение и расстояние точки от плоскости.
n1x+n2y+n3z+n4=0
n={n1; n2; n3}
-- нормирующий множитель.
Знак
выбирается таким образом, чтобы μ*n4<0.
Если n4=0,
то μ*n1>0.
отсюда получаем, что – нормирующее
уравнение плоскости. Следовательно:
Отсюда получаем Теорему об отклонении и расстоянии точки от плоскости.
Пусть n1x+n2y+n3z+n4=0 – уравнение плоскости α.
-- нормирующий множитель.
n={n1; n2; n3}
Тогда отклонение точки от плоскости находят по формуле:
d(M;α)=|σ| -- расстояние
Уравнение плоскости делит пространство на 3 непересекающихся множества:
σ(М)=0 – множество точек плоскости
σ(М)>0 – множество точек с положительным отклонением от плоскости
σ(М)<0 – множество точек с отрицательным отклонением от плоскости. Лежат с одной и той же стороны, что и начало координат, если плоскость не проходит через 0.
25. Угол между плоскостями. Условие параллельности и перпендикулярности плоскостей.
n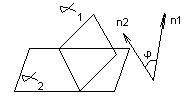
1
и n2
– нормальные вектора плоскостей α1
и α2.
Угол между плоскостями
определяется как двугранный угол. Его
мерой является линейный угол. Поэтому
в качестве угла можно взять угол между
n
1
и n2.
n1 * n2 = 0 – условие перпендикулярности
n1 = λn2 – условие параллельности
У
гол
между прямой и плоскостью.
n – нормальный вектор плоскости
S – направляющий вектор
cosα=cosφ
φ
– угол между прямой и плоскостью
n*S=0 – условие параллельности
n=λS – условие перпендикулярности