15. Косинус угла между векторами. Орт и модуль вектора. Направляющие косинусы вектора.

Косинус угла между векторами.

φ = -- определяется как угол между прямыми ОА и ОВ.

Косинус угла в пространстве Rⁿ определяется по формуле:

Покажем, что определение косинуса угла совпадает с обычным косинусом φ на плоскости и в трехмерном пространстве.

a ₀={1;0}

b₀={cosφ; sinφ}

a₀*b₀=cosφ+0*sinφ=cosφ

a₀*b₀=cosφ

Для ненулевых векторов из свойств СПР получаем:

φ – тупой  a*b<0

φ – острый  a*b>0

φ = 90^о  a*b=0

φ =  a*b=0 – Это условие перпендикулярности векторов.

Направляющие косинусы вектора.

Пусть α_k – угол между лучом (ОА) и координатной осью x_k (k=1, 2, …, n)

α_k= =

Нетрудно доказать для единичного вектора следующую формулу:

cosα_k…cosα_n – направляющие косинусы вектора.

Орт и модуль вектора.

Модуль вектора(длина вектора):

Если вектор определен 2 точками, то модуль – длина между этими точками:

Если вектор разделить на модуль, то получаем единичный вектор, который называют ортом вектора. Этот вектор задает направление и определяется по формуле.

Это направляющие косинусы вектора. α1, α2, …, αn – углы, образованные а с осями координат. Отсюда получаем свойства для единичных векторов:

16. Векторное произведение векторов: определение и геометрический смысл

Определим векторное произведение векторов в 3-х мерном пространстве, которое будет определять вращение в этом пространстве. Векторное произведение:

Ч тобы получить координаты нового вектора, надо разложить его по первой строке: .

Выясним геометрический смысл этого произведения. Берем координаты следующим образом:

| a|=a

|b|=b

φ=a^b

a={a;0;0}

b={b*cos φ;b*sin φ;0}

Найдем векторное произведение .

.

Единичный вектор перпендикулярный плоскости параллелограмма. С конца этого вектора видим вращение а к b по углу φ против часовой стрелки.

Модуль векторного произведения – площадь параллелограмма, построенного на векторах а и b.

Физический смысл векторного произведения:

Пусть О – точка вращения твердого тела

А – точка, где к телу приложена сила F.

Тогда момент этой силы можно рассчитать по формуле:

M=OA x F

ОА – плечо силы

|M|=|OA|*sinφ*|F|.

17. Основные свойства векторного произведения

1. -- антикоммутативность.

Следует из определения векторного произведения, т.к. переставляя множители местами, переставляем строки в определителе.

2. -- дистрибутивность

Вывод:

3. , где λ R.

18. Смешанное произведение. Основные свойства и геометрический смысл

В 3-х мерном пространстве смешанное произведение 3-х векторов:

( 1) Разложим определитель по 1-й строке:

Иногда это свойство принимают в качестве определения. Тогда формулу (1) надо доказать. Теперь нетрудно показать геометрический смысл смешанного произведения.

, где V – объем параллелепипеда. Покажем это:

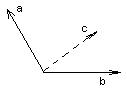
h – высота параллелепипеда.

Определение ориентации в пространстве:

если , то векторы образуют правую тройку, при этом говорят, что они имеют положительную ориентацию.

если , то векторы образуют левую тройку, при этом говорят, что они имеют отрицательную ориентацию.

Рассмотрим ориентацию стандартного базиса:

Стандартный базис имеет положительную ориентацию.

Если вектора линейно зависимы, то они называются компланарными. Условие компланарности векторов:

Если в смешанном произведении 2 вектора переставить местами(рядом стоящие), то знак изменится.

При циклической перестановке знак не меняется:

Выбирая 3 последовательных множителя они образуют циклическую перестановку.