26. Деление отрезка в данном отношении

АМ = λ*АВ – условие коллинеарности векторов

λ – отношение

П о этим формулам находим точку М.

λ =0, 5 :

λ=0 => M=A

λ=1 => M=B

λ>1 => М правее В

λ<1 => М левее В

В треугольнике точка пересечения медиан О(x; y; z) имеет координаты:

27. Уравнение прямой на плоскости

Н етрудно вывести следующую формулу для прямой, проходящей через точки А и В или имеющей направляющий вектор S.

Делается это также как и в пространстве.

АМ = λ*АВ

-- параметрическое уравнение прямой

S={S1; S2} – направляющий вектор прямой.

АМ = λ*S

И сключая параметр, получаем каноническое уравнение прямой, проходящей через А в направлении вектора S.

У равнение прямой с угловым коэффициентом.

В(0; b)

b – начальная координата

k=tgφ – угловой коэффициент

М(x; y) – текущая точка

ВМ=λ*ВА – параметрическое уравнение прямой l.

А(1; b+ tgφ)

B(0; b)

BA={1; tgφ}

Отсюда получаем новое уравнение прямой:

y=kx+b – с угловым коэффициентом k.

28. Нормальное уравнение прямой на плоскости. Отклонение точки от прямой.

Пусть А – точка на прямой

n – нормальный вектор

А(0; 0)

n={n₁; n₂} M(x; y)

Уравнение прямой получаем из условия перпендикулярности векторов:

АМ*n=0

Р аскрывая скобки, получаем:

Прим.:

Найти уравнение прямой:

А(5; 1)

п ерпендикулярно прямой 3x+12y=12

n₂={1; 4}

n₁={1;4}

n={3; 12}

4x-y-19=0

Отклонение и расстояние точки от прямой:

l – данная прямая

n – нормаль

n0={cosα; cosβ}

|OA|=p

OA=p*n₀

σ(M; l)=AM*n₀

σ=OM*n₀-p

σ(M; l)=xcosα+ycosβ-p= xcosα+ysinα-p

d=| σ |

Чтобы найти отклонение М от прямой надо подставить ее координаты в левую часть нормального уравнения прямой. Найдем отклонение начала координат:

σ=-p

d=p

Если прямая не проходит через начало координат, то отклонение всегда будет отрицательное. Прямая делит всю плоскость на 3 непересекающихся множества.

Н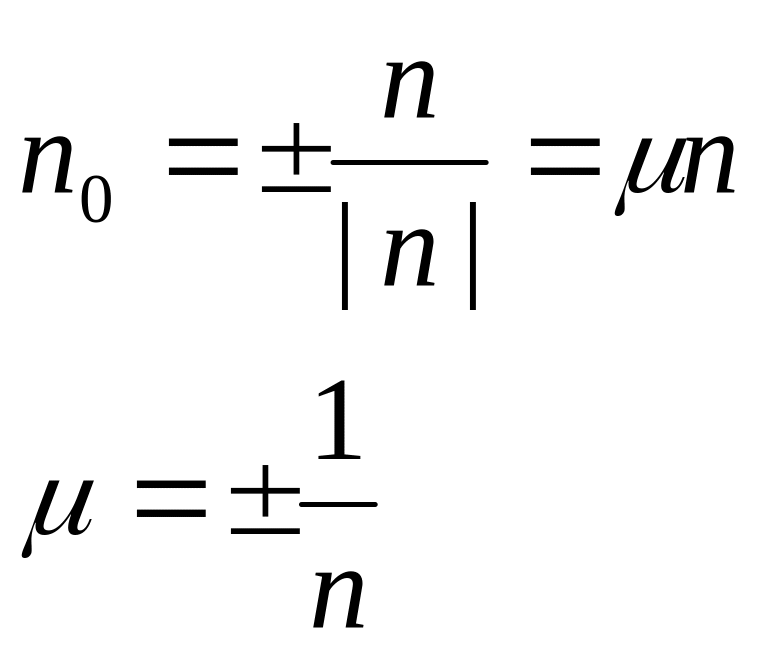 етрудно показать, что единичный вектор:

-- нормирующий множитель.

Умножим общее уравнение на нормирующий множитель.

Таким образом доказана прямая об отклонении точки от прямой.

П усть n₁x+n₂y+n₃=0

n={n₁; n₂}

29. Угол между прямыми на плоскости условие параллельности и перпендикулярности прямых.

S ₁, S₂ – направляющие векторы прямых

Тогда угол можно определить, как угол между направляющими векторами.

S₁=λS₂ – условие параллельности прямых

S₁*S₂=0 – условие перпендикулярности прямых

Аналогично угол можно определить как угол между нормальными n₁ и n₂ и получить такие же формулы.

Рассмотрим уравнение прямых с угловым коэффициентом:

y =k₁x+b₁(φ₂=φ₁+φ)

y=k₂x+b₂(φ₂=φ₁-φ)

И спользуя формулу tg разности:

Отсюда получаем формулу:

Если прямые параллельны, то k₂-k₁=0

Если прямые перпендикулярны, то tgφ=tg90^o=>Ø 1+k₁*k₂=0

Отсюда получаем условия перпендикулярности и параллельности:

k₁=k₂ – условие параллельности

k₂*k₁=-1 – условие перпендикулярности