6. Равномерная сходимость. Свойства равномерно сходящихся рядов
Определение
1.4. Ряд
(1.1) называется равномерно сходящимся
рядом в некоторой области D,
если в этой области последовательность
частичных сумм
(1.3)
сходится
равномерно к своей предельной функции S(x):
Теорема
Вейерштрасса. Функциональный
ряд (1.1), каждый член которого является
функцией, определенной в некоторой
области D,
сходится равномерно в этой области,
если существует такая
последовательность 
положительных
постоянных, что выполняется неравенство
(1.2) для любого 
и
любого n=1,2,…,
а ряд
(1.4) сходится.
Доказательство. Из
(1.2) и (1.4) на основании первого признака
сравнения следует сходимость
функционального ряда (1.1) в каждой точке
области D к
функции S(x).
В силу сходимости ряда (1.4) (обозначим
его сумму через S)
возьмем произвольное 
и
найдем по нему такое n0,
что при n>n0 выполняется
неравенство
, то
есть
(1.5)
Для
этого n имеет
место равенство
(1.6)
где 
Из
неравенств (1.2), (1.5) и равенства (1.6)
следует, что 
при
любых 
и 
Таким
образом, по каждому 
находим
такое n0,
что при
имеет
место неравенство 
при
любом x.
Это и означает равномерную сходимость
ряда. Теорема доказана.
Теорема 1.2. Если функциональный ряд (1.1) сходится в некоторой области D равномерно и абсолютно, а функцииfn (n=1,2,…) в этой области равномерно ограничены в совокупности, то ряд
(1.7) также
сходится в этой области равномерно и
абсолютно.
2. Свойства равномерно сходящихся рядов.
Теорема 2.1. Пусть все члены функционального ряда (1.1) определены в некоторой области D, непрерывны в ней и составленный из них функциональный ряд сходится в этой области равномерно. Тогда суммой ряда (1.1) будет функция, непрерывная в области D.
Доказательство. Из непрерывности членов функционального ряда (1.1) следует непрерывность каждой из его частичных сумм (1.3). По условию эта последовательность частичных сумм сходится равномерно к предельной непрерывной функции S(x), являющейся суммой ряда (1.1). Теорема доказана.
Теорема 2.2. (Почленное интегрирование ряда). Если функциональный ряд (1.1) сходится равномерно в некоторой области D и имеет сумму S(x), то функциональный (относительно переменной у) ряд интегралов
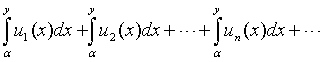(2.1) (здесь 
)
также сходится равномерно в этой области
и имеет суммой функцию
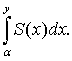(2.2)
Определение 2.1. Переход от ряда (1.1) и его суммы к ряду (2.1) и его сумме называется почленным интегрированием ряда.
Пример 2.1. Найти сумму ряда
(2.5)
Решение. Этот
функциональный ряд сходится равномерно
при 
и,
как легко видеть (этот ряд является
геометрической прогрессией), сумма его
равна 
Следовательно,
получаемый почленным интегрированием
ряда (2.5) от 0 до x<1 ряд
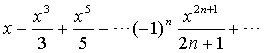
также
равномерно сходится при
и
его сумма равна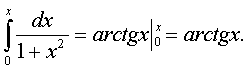
Итак, S(x)=acrtgx.
Теорема
2.3. (Почленное
дифференцирование ряда). Пусть
ряд (1.1) сходится в некоторой области D и
имеет сумму S(x),
а его члены имеют в этой области
непрерывные производные, тогда
составленный из этих производных ряд
(2.6) сходится в D
равномерно, и производная его суммы
равна сумме ряда (2.6):
Доказательство. Пусть Sn(x) – n-я частичная сумма ряда (1.1). Тогда
будет, очевидно, n-ой частичной суммой ряда производных (2.6). По условию теоремы последовательность частичных сумм (1.3) сходится в области D, а последовательность
(2.7)
частичных сумм также сходится в этой
области и притом равномерно. Следовательно,
на основании теоремы о переходе к пределу
под знаком производной последовательность
(2.6) сходится равномерно и производная
ее предела равна пределу последовательности
(2.7). Теорема доказана.
Определение 2.2. Переход от ряда (1.1) и его суммы к ряду (2.6) и его сумме называется почленным дифференцрированием ряда.