2. Ряды с положительными членами. Признаки сходимости.
Признаки сравнения
Если 
,
и ряд 
сходится,
то сходится и ряд 
.
Если , и ряд расходится, то расходится и ряд .
Признаки сравнения можно сформулировать в такой форме:
Если
заданы ряды
,
и
существует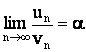 
,
то ряды
и
сходятся
либо расходятся одновременно.
Пример:
Исследовать
сходимость ряда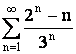 
.
Имеем: 
.
Ряд 
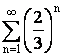сходится
как сумма геометрической прогрессии
со знаменателем 
.
Следовательно, согласно признаку
сравнения ряд
сходится.
Признак Д’Аламбера
Если
существует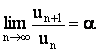 
то:
- при 
ряд
сходится;
- при 
ряд
расходится.
Радикальный признак Коши
Если
существует 
то:
- при
ряд
сходится;
- при ряд расходится.
Интегральный признак Коши
Пусть
задан ряд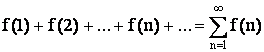 
,
члены которого являются значениями
непрерывной, положительной и монотонно
убывающей функции 
на
промежутке 
.
Тогда ряд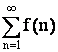 
сходится,
если сходится несобственный интеграл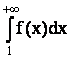 
.
Если же
расходится,
то ряд
также
будет расходящимся.
4. Знакочередующиеся ряды. Теорема Лейбница.
Ряд называется знакочередующимся,
если его члены попеременно принимают
значения противоположных знаков,
Признак Лейбница (достаточный признак сходимости знакочередующихся рядов)
Ряд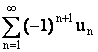 
сходится,
если:
- 
;
- 
.
Знакопеременный
ряд
называют абсолютно
сходящимся, если сходится ряд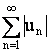 
Если ряд сходится, а ряд расходится, то ряд называют сходящимся условно.
Очевидно, что если ряд сходится, то ряд также сходится. Обратное утверждение в общем случае неверно.
Исследовать
ряд на сходимость 
Используем признак Лейбница:
1) 
Ряд
является знакочередующимся.
2) 
–
члены ряда убывают по модулю.
Вывод: ряд сходится.
Исследуем
наш ряд на абсолютную сходимость.
–
расходится (гармонический ряд).
Таким образом, наш ряд не является абсолютно сходящимся. Исследуемый ряд сходится только условно.
5. Функциональные ряды. Область сходимости
Рассмотрим
ряд, 
,
членами которого являются функции,
определенные на промежутке 
.
При каждом фиксированном 
имеем
числовой ряд, сходимость которого может
быть исследована рассмотренными ранее
методами. Сумма функционального
ряда
также
является функцией от х: 
.
По определению предела последовательности:
если для 
можно
указать номер 
(
что интересно, для каждого фиксированного
- свой номер, т.е. 
),
такой, что для 
выполняется
неравенство 
,
то это и означает, что функциональный
ряд сходится к функции
.
Множество 
,
для которого это выполняется, называется
областью сходимости функционального
ряда.
Признак д’Аламбера
Ряд 
Сходится абсолютно, если 
Расходится,
если 
Существуют
как сходящиеся, так и расходящиеся ряды,
для которых 
Интегральный признак Коши — Маклорена
Пусть
задан ряд 
и
функция 
такая,
что:
f(x) нестрого
монотонно убывает: 
Тогда
ряд 
и
интеграл 
сходятся
или расходятся одновременно, причем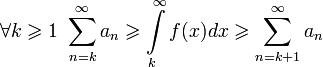 
Пример
9. Найти область сходимости функционального
ряда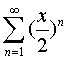 
.
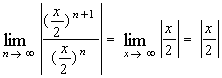Решением
неравенства 
является
интервал (-2;2).
Исследуем сходимость ряда на границах: при х=-2 и при х=2.
Если
х=-2, то ряд 
расходится,
так как не выполнено необходимое условие
сходимости. Тот же результат получим
при х=2. Следовательно, областью сходимости
ряда является интервал (-2,2).