
- •1. Четыре периода в развитии математики.
- •2. Возникновение понятия числа.
- •3.Система счисления и вычислительная техника египтян.
- •5. Вычислительная техника вавилонян.
- •16. История теоремы Пифагора.
- •20. Построение правильного пятиугольника в «Началах» Евклида.
- •36. Правило двух ложных положений (Китай)
16. История теоремы Пифагора.
Сумма площадей квадратов, построенных на катетах прямоугольного треугольника равна площади квадрата, построенного на гипотенузе. с2 = a2 + b2.
Название говорит, что теорему приписывают Пифагору. Теперь известно, что её знали задолго до Пифагора. За 12 в. в Др. Вавилоне, за 22в. в Др. Китае. Возможно Пифагор узнал эту теорему, путешествуя по Др. Египту и Др. Вавилону, а может быть в Милетской школе Фалеса. Однако есть свидетельство в пользу того, что она доказана впервые в школе Пифагора.
Существует легенда, что в честь посетившей его идеи, Пифагор принёс в жертву богам 100 быков. И ходит анекдот, что с той поры все скоты не любят математику. Док-во Пифагора не сохранилось, но к настоящему времени известно огромное число док-в.
Один из античных исследователей математики утверждает, что док-во самого Пифагора основано на идее подобия треугольников.
1). Док-во, основанное на идее подобия.
1). АСН АВС
АН/АС = АС/АВ => АС2 = АВАН
2![]() ).СНВАВС
=> H
).СНВАВС
=> H![]() B/CB
= CB/AB
=> CB2=ABHB
B/CB
= CB/AB
=> CB2=ABHB
AC2 + BC2 = ABAH + ABHB = AB(AH + HB) = AB2
AB2 = AC2 + BC2 ч.т.д.
2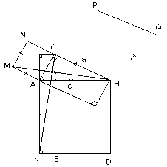 ).
Док-во Евклида.
).
Док-во Евклида.
Доп. построения:
1. [MB), [KC)
2. (CE) (KD)
Док-во:
1). Рассмотрим АМВ и АСК:
МА = АС, АВ = АК, МАВ = КАС = + 900
Следовательно, АМВ = АCK по 2 сторонам и углу м/у ними.
2). Имееv: SАМВ = SАCK
![]()
![]()
Следовательно, 1/2b2 = 1/2AKKE => b2 = SKALE
Аналогично, SLBDE = a2. Тогда, c2 = a2 + b2
3). Док-во, основанное на алгебраических док-вах:
- Школьное док-во.
Школьное док-во.
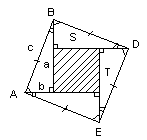
- Док-во Агарья Бкаскара (Индия, XIIв.)
Доп. построения:
1. ABDE - квадрат
2. АК ВС
3. ES DK
Имеем АТ ES
Док-во:
1). АВС = BKD = ESD = ATE (по гипотенузе и острым углам)
2). SABDE = SCKST + 4SABC
c2 = (a – b)2 + 41/2ab
c2 = a2 – 2ab + b2 + 41/2ab
c2 = a2 + b2 ч.т.д.
- Построение: АВ = а, ВС = b, AK AB, AK = b, CN BC, CN = a,
A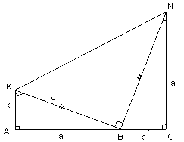 KNC
– трапеция, [KB],
[NB]
KNC
– трапеция, [KB],
[NB]
Док-во:
1). AKB = BNC => KB = NB = с
2). KBN – прямоуг, т.к. KBN=1800-(+)=900

a2 + 2ab + b2 = 2ab + c2
a2 + b2 = c2 ч.т.д.
20. Построение правильного пятиугольника в «Началах» Евклида.
П![]() редложение
11.
Данную прямую рассечь так, чтобы
прямоугольник, заключённый между целой
и одним из отрезков был равен квадрату
на оставшемся отрезке.
редложение
11.
Данную прямую рассечь так, чтобы
прямоугольник, заключённый между целой
и одним из отрезков был равен квадрату
на оставшемся отрезке.
Построение:
1. ABDM - квадрат
2. Е: АЕ = EM
3. [EB]
4. I: I[MA], EI = EB
5. C: C[AB), AC = AI
C – золотое сечение. АС2 = АВВС
П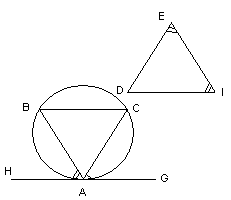 редложение
2.
В данный круг вписать треугольник,
равноугольный данному треугольнику.
редложение
2.
В данный круг вписать треугольник,
равноугольный данному треугольнику.
Построение:
1. А – произвольная точка
2. HG: HG – касат., АHG
3. CAG = DEI
BAH = DIE
4. [BC]
5. ABH – искомый.
П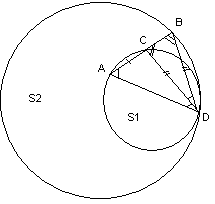 остроение
золотого треугольника
– равнобедренный треугольник, углы при
основании которого в 2 раза больше угла
при вершине.
остроение
золотого треугольника
– равнобедренный треугольник, углы при
основании которого в 2 раза больше угла
при вершине.
Построение:
1. [AB]
2. C: C[AB], C – золотое сечение.
АС2 = АВВС
3. S: S(A, AB)
4. [BD], D S, AC = BD
5. [AD]
ABD – золотой.
Док-во:
Доп. Построения:
1). [CD], 2). S1: S1(A, CD)
1). АС2 = АВВС и AC = BD (по построению) => ABBC = BD2 => BD – касательная. (по теореме обратной предложению: если ВА – секущая, BD – касательная, то ABBC = BD2).
2). BDC = , CDA =
DCB – внешний для ACD => DCB = +
Т.к. AВD равнобедренный, то AВD = ADB = +
Следовательно, СВD – равнобедренный, СD = BD.
3). Имеем СD = BD и BD = АС => AC = CD => ACD – равнобедренный => =
4). Имеем в AВD: A = , B =D =2 => AВD – золотой.
П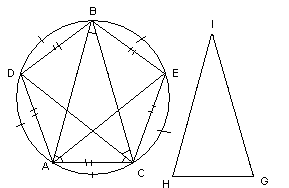 остроение
правильного пятиугольника.
остроение
правильного пятиугольника.
1. АВС HGI
2. AE и CD – биссектриса А и С
3. ADBEC – правильный пятиугольник.
Док-во:
1. AB = BC, A=C=2, B =
2. AE и CD – биссектриса А и С.
Дуги равны, т.к. опираются на равные углы => ADBEC – равносторонний
3. Любой из углов опирается на дугу, состоящую из 3-х равных дуг => пятиугольник правильный.
30 Число. (Древний Китай) О А
Ученый-полководец
Ван-Фань получил лучшее приближение
В комментариях к «Математике в 9 книгах» приводится один способ вычисления приближенного значения , который состоит в следующем: Впишем в окружность правильный n-угольник и на его сторонах построим прямоугольники, один из сторон которых касается окружности.
|
![]()
![]()
![]()
![]()
![]()
Лю Хуэй (III
в до н.э.) полагая
![]()
При ![]() , он находит, что
, он находит, что![]()
Цзу Чуы-Чжи
(V
в) доказал,
что ![]()
Точность приближения числа , указанная китайскими математиками, была превзойдена лишь в XV веке математиком Ал-Каши в трактате «Об окружности». Он вычислил значение числа с 17ю верными знаками

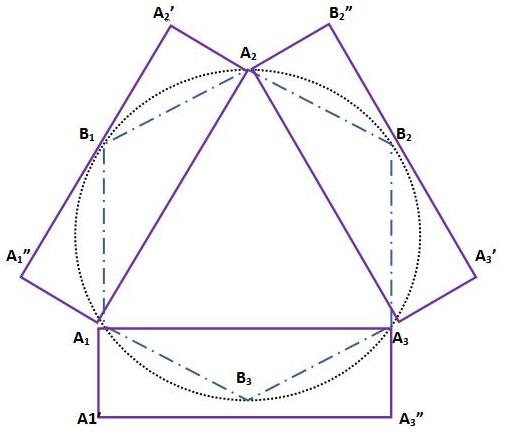 собенностью
китайской геометрии является стремление
вычислить как можно более точно
отношение длины окружности к диаметру,
то есть, число .
собенностью
китайской геометрии является стремление
вычислить как можно более точно
отношение длины окружности к диаметру,
то есть, число .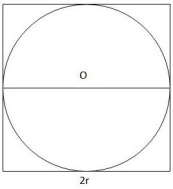 строном
и философ Чжан
Хен (II
в до н.э.)
нашел, что «квадрат длины окружности
относится к квадрату периметра
описанного около него квадрата как
5:8
строном
и философ Чжан
Хен (II
в до н.э.)
нашел, что «квадрат длины окружности
относится к квадрату периметра
описанного около него квадрата как
5:8