5. Вычислительная техника вавилонян.

К достоинствам вавилонской позиционной системы относятся принцип позиционности и характер основания системы – числа 60, которое имеет достаточно большое количество целых делителей. В то же время число 60 велико и приводит к существенным затруднениям при умножении и делении.

Все арифметические операции формулировались словесно, и для каждого действия имелись свои специальные термины, причем не по одному.

Сложение. Два термина: «складывать» и «прибавлять». Термин «складывать» употреблялся для двух равноправных величин, таких, как длина и ширина прямоугольника; «прибавлять» - использовался для двух величин, одна из которых играла роль основной, а другая подчиненной. Например, если известна разность между длиной и шириной прямоугольника и его ширина, то для нахождения длины прямоугольника к его ширине прибавляют известную разность. В дальнейшем мы будем использовать термин gar (га) - «складывать». При сложении числа между разрядами 1, 60, 60² , … складывались приписыванием, а затем осуществлялся переход от разрядов к разрядам с учетом того, что десять единиц дают один десяток.

В ычитание: «превышать», «недоставать» и «отнимать». Мы исползуем термин lal «недоставать», как отрицание для «складывать». Термин «недоставать» или «минус» имел спец. символ . Он часто использовался и для записи чисел, оканчивающихся на 7, 8 и 9. Например, число 19 записывалось двумя способами:

=10 + 9 или = 20-1

Д ля операции умножения на 2 использовался термин tab (таб). Он также исполнял роль противостояния термину lal «минус». Позднее, в астрономических текстах значки «лал» и «таб» использовались как наши « - » и «+» для обозначения отрицательных и положительных чисел. Они ставились после числа. Приведем таблицу чисел из астрономического текста.

Если построить точки с равномерным интервалом по оси абсцисс и соединить их плавной линией, то эта линия будет иметь волновой вид;в да далекие времена она могла служить для описания периодических процессов.

Умножение: «умножить», «увеличить», «кушать». Наиболее компактная таблица умножения в десятичной системе (без умножения на 1 и с учетом коммутативности) имеет вид:

Она содержит 36 произведений (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 =

Аналогичная таблица в шестидесятеричной системе имела бы 1711 произведений. Такую таблицу запомнить невозможно, поэтому вавилоняне составляли неполные (или отдельные) таблицы умножения. Одно и то же число (заглавное) последовательно умножалось на 1,2, …, 18, 19, 20, 30, 40, 50. Заглавное число (множимое) указывалось один раз в первой строке, а в остальных отмечался только множитель. При этом клинописный знак , который читается a – ra (ара) и соответствует в русском языке частицам «жды» или «ю», устойчиво записывался в каждой строке. Приведем фрагмент таблицы умножения на 7.

П 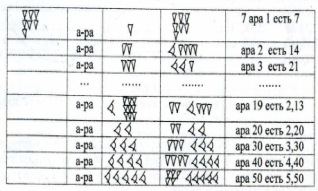о аналогии с современной школьной таблицей умножения можно было ожидать, что в состав заглавных чисел войдут все целые числа от 1 до 59. Однако это не так. Все заглавные числа, за исключением 7, являются так называемыми правильными числами: , где При этом правильных чисел 27, 32 и 54 не обнаружено, но есть некоторые двузначные числа и одно трехзначное число: 44,26,40₆₀.

Деление: «разбить», «разломать», «часть», «дробь» и т.д. Вавилоняне частное воспринимали как число, которое должно быть умножено на делитель, чтобы получить делимое. Для нахождения частного надо: пусть надо разделить a на b. Вав. находили число и умножали a на . Значение b находилось из специально составленных таблиц обратных значений.

Л евый столбец содержит все правильные числа n в интервале от 1 до 1,21₆₀, т.е. от 1 до 81, а правый – числа , такие, что . Первая строка означает 1/2 = 0;30, вторая строка - 1/3 = 0;20, третья строка - 1/4 = 0;15 и т.д. В шестой строке запись 8 - 7,30 (обратное 8 есть 7,30) нужно понимать так: = 7/60 + 30/60² = 1/8. В последней строке читаем: обратное 1,21 есть 44,26,40. Это означает следующее: 1/81 = 0;00,44,26,40. Итак, в данную таблицу вошли только натуральные числа вида . Именно они, имеют обратные, представимые конечной шестидесятеричной дробью. Числа, обратные пропущенным (7, 11, 13,14,17,…, 35 и др.) - бесконечными периодическими 60-ричными дробями. В некоторых таблицах есть и эти числа, но во втором столбце запись: «нет обратного». В более поздних таблицах для неправильных чисел даются приближенные значения обратных чисел. Дробь оказывается периодической, причем вавилоняне выписывали период дважды. Они должны бы придти к идее периодич. 60-ричной дроби, но указаний на это в текстах нет. Таблицы обратных значений и таблицы умножения тесно взаимосвязаны между собой. На это указывает наличие среди заглавных чисел в таблицах умножения трехзначного числа 44,26,40 , которое является последней обратной величиной в таблице обратных значений. Совокупность этих таблиц составляет законченную систему, предназнач. для вычисления всех произведений или всех 60-ричных делений a/b в пределах таблицы обратных величин.

Впервые в истории человечества вавилоняне использовали позиционную 60-ричную систему счисления. До сих пор мы пользуемся элементами этой системы, деля час на 60 минут, минуту – на 60 секунд, секунду – на 60 терций, окружность – на 360⁰. Вавилоняне владели высоким вычислительным искусством. Только одна система таблиц умножения и обратных величин ставит их впереди всех вычислителей античного мира.

. 12 Стереометрия в Древнем Египте.

Египтянам необходимо было вычислять объёмы фигур цилиндрической, конической, пирамидальной и параллепипедной формы. Эти знания им были необходимы при строительстве амбаров и всевозможных укреплений. Нужно было знать, например, сколько зерна войдёт в амбар. Источники свидетельствуют о том, что объём цилиндра, куба, параллепипеда, призмы вычислялись как произведение площадей оснований на высоту. Вершиной все египетской математики является открытие точного способа вычисления объёма усечённой пирамиды с квадратным основанием.

V = h/ 3  (a²+ab+b²)

О получении этой формулы в папирусах ничего не сказано, однако трудно предположить, что она было получена эмпирически. Это можно сделать только логическим путём с использованием геометрических и арифметических рассуждений.

Рассмотрим задачу № 14. «Форма вычисления усечённой пирамиды когда тебе называют усечённую пирамиду высотой 6 локтей с плоскостями по 4 локтя на нижней стороне и по 2 локтя на верхней стороне. Реконструкция решения:

Текст первоисточника	Решение	Формулы в общем виде
Считай ты с этой четверти возведённой в квадрат, чтобы запомнить. Получается 16.	42 = 16	а2
Удвой и получается 8.	42=8	аb
Считай ты с этой двойной, возведённой в квадрат, чтобы запомнить. Получается 4.	22 = 4	b2
Сложи вместе эти 16 с этими 8 и с этими 4. Получается 28.	16 + 8 + 4 = 28	a2 + ab + b2
Считай 1/3 от 6. Получается 2.	1/3  6 =2	1/3  h
Считай ты с 28-го 2 раза. Получается 56.	2  28 = 56	h/3  (a2 + ab + b2)

Смотри, это равно 56. Ты правильно нашёл.

В задаче указан алгоритм решения, но нет никаких указаний на то, почему именно так надо действовать. Отто Нейгебауер предложил следующий вывод этой формулы для усечённой пирамиды частного вида.

Объём данной усечённой пирамиды складывается из объёмов параллепипеда, пирамиды и двух призм.

При такой реконструкции следует постулировать умение египтян выполнять некоторые алгебраические преобразования. Например, знать формулу (a + b)² = a² + ab + b². Между тем, явных подтверждений того, что они этим владели, в источниках нет. А. Е. Рейн полагает, что египтянин-математик получил этот результат гораздо проще.

В А₁В₁С₁D₁, D₁ABCD – пирамиды

Естественно возникает вопрос, как древние египтяне установили, что объём пирамиды равен 1/3 объёма соответствующей ей призмы. В египетских источниках нет ответа на этот вопрос, но наиболее вероятно, что объём пирамиды был найден эмпирически, например, сравнением вместимости пирамиды и призмы.

Задача из папируса М10. «Форма вычисления корзины, если тебе называют корзину с диаметром устья 4 2. О дай мне узнать её поверхность».

Текст первоисточника		Вычисления	Формула в общем виде
Вычисли 9 от 9, т.к. корзина половина яйца. Получится 1.		4 2. 9 9 = 1	d 1/9 2d
Вычисли остаток. Это 8.		9 – 1 = 8	2d – 2d/9
	Вычисли 1/9 от 8. Получится 2/3, 6,18
	Вычисли остаток от этих 8, 3,6,18. Получится 79.
	Вычисли 79 умноженную на 4 2. Смотри, это и есть её поверхность, ты правильно её нашёл.

S_сф = 4r²

S_п/сф = 2r² = 2S_круга