5.5. Розподіл функцій між людиною-оператором. І технічними засобами аск

Вивчення досвіду впровадження АСК у різноманітних сферах переконує нас у тому, що провідна роль у цих системах зали­шається за людиною-оператором. Фактично обсяг так званої рутинної роботи, якою доводиться займатись управлінському персоналові, не зменшується з впровадженням у процес керу­вання ЕОМ. Однак використання ЕОМ у керуванні корінним чином змінює форми розумової праці людини. Концепція повної автоматизації переробки інформації не витримує сьогодні випробування часом у зв'язку із завданням творчого характеру.

Звідси випливає необхідність виділити окремо завдання, що розв'язує людина-оператор, і завдання, що розв'язує ЕОМ. На основі цього вирішується питання, які завдання передаються в системі технічним засобам разом з ЕОМ, і які на відповідному етапі розвитку АСК залишаються за людиною. Особливого значення набуває тут аспект взаємодії людини і ЕОМ у розв'язуванні завдань, процес вирішення яких виявляється поді­леним між людиною і ЕОМ.

Розподіл функцій керування в АСК має базуватися, по-перше, на інженерно-психологічній оцінці та використанні вислі-дів вивчення психічних здібностей людини, по-друге, на систем­ному підході до використання ЕОМ. Таким чином, об'єктами у розподілі функцій керування на певному етапі розвитку АСК є: множина завдань, що розв'язуються в системі керування; множи­на функцій, що виконуються при розв'язуванні цих завдань; опе­ративний апарат або окремий оператор; технічні засоби АСК (ЕОМ).

Визначальний фактор у розподілі функцій — набір парамет­рів людини й ЕОМ, які характеризують якість виконання покла­дених на них функцій (табл. 5.1).

Показник	Людина	ЕОМ	Людина+ЕОМ
Здатність працюва­ти в несподіваних ситуаціях Робота з непов­ною інформацією Вибір способу дії Швидкість виконання обчислень Точність виконання операцій Надійність Працездатність	Висока гнучкість і здатність пристосовуватися Здатна відтворити цілісну подію Великі можливості вибору Порівняно мала Низька Низька Залежить від втоми	Практично неможливо запрограмувати всі випадковості Практично неможлива Обмежені можливості вибору Висока Довільна Задовільна Постійна	Людина комбінує програми і методи, скориговує роботу системи Людина корегує роботу ЕОМ Людина вибирає дії, єом їх реалізує Людина координує обчислення Визначається алгоритмом Вища ніж у компонентів системи ЕОМ «підстраховує людину», допомагає їй

Динамічні завдання задачі управління запасами.

Однією з найбільш відомих сфер додатку методів динамічного програмування є така область математичної економіки, як теорія управління запасами. Її предметом є розробка і дослідження математичних моделей систем, що займають проміжне положення між джерелами (виробниками) тих або інших ресурсів і їх споживачами. При математичній формалізації процесів управління запасами дуже часто доводиться використовувати стрибкоподібні функції, що не диференціюються і кусочно-безперервні. Як правило, це обумовлюється необхідністю обліку ефектів концентрації, фіксованих витрат і плати за замовлення. У зв'язку з цим отримувані завдання насилу піддаються аналітичному рішенню класичними методами, проте можуть бути успішно вирішені за допомогою апарату динамічного програмування. Розглянемо достатньо типове завдання, що виникає в процесі планування діяльності системи постачання, — так зване динамічне завдання управління запасами.

Хай є деяка система постачання (склад, оптова база і т. п.), плануюча свою роботу на періодів. Її діяльність зводиться до забезпечення попиту кінцевих споживачів на деякий продукт, для чого вона здійснює замовлення виробникові даного продукту. Попит клієнтів (кінцевих споживачів) в даній моделі розглядається як деяка інтегрована величина, що набуває заданих значень для кожного з періодів, і він повинен завжди задовольнятися (тобто не допускаються заборгованості і відмови). Також передбачається, що замовлення, що посилається виробникові, задовольняється ним повністю, і часом між замовленням і його виконанням можна нехтувати (тобто розглядається система з миттєвим виконанням замовлення). Введемо позначення:

— залишок запасу після (k-1) -го періоду;

— заздалегідь відомий сумарний попит в -м періоді;

— замовлення (постачання від виробника) в -м періоді;

— затрати на виконання замовлення об'єму в -м періоді;

— зберігання запасу об'єму у -м періоді.

Після отримання постачання і задоволення попиту об'єм товару, підлягаючого зберіганню в період к, складе . Враховуючи сенс параметра , можна записати співвідношення:

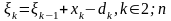(5.24)

Витрати на отримання і зберігання товару в період описуються функцією

.

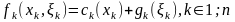За план завдання можна вважати вектор компонентами якого є послідовні замовлення протягом даного проміжку часу. Співвідношення між запасами (5.24) у поєднанні з деякою початковою умовою пов'язує стани системи з вибраним планом і дозволяє виразити сумарні витрати за всі періодів функціонування| керованої системи постачання у формі|у формі| адди­тивної| цільової функції:

(5.25)

Природним в рамках сформульованої моделі представляється завдання знаходження послідовності оптимальних управлінь (замовлень) і зв'язаних з ними оптимальних станів (запасів) , які обертають в мінімум (5.25). Як початкова умова використовуємо вимогу про збереження після завершення управління заданої кількості товару , а саме

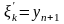(5.26)

При рішенні поставленої задачі методом динамічного програмування як функція стану керованої системи логічно узяти мінімальний об'єм витрат, що виникають за перших до періодів за умови, що в -й період є запас . Тоді можна записати основне рекурентне співвідношення

(5.27)

Оскільки

Система рекуррентних співвідношень (5.27)-(5.28) дозволяє знайти послідовність функцій стану і умовних оптимальних управлінь На м кроці за допомогою початкової умови (5.26) можна визначити . Інші значення оптимальних управлінь визначаються за формулою:

(5.29)

Особливий інтерес представляє окремий випадок завдання (5.24) -(5.25), при якому передбачається, що функції затратна поповнення запасу є увігнутими по , а функції витрат на зберігання є лінійними щодо об'єму запасу, що зберігається, тобто . Паралельно відмітимо, що обидві передумови є достатньо реалістичними.

Позначимо функцію витрат|затрат| протягом -го періоду через

(5.30)

або, що те ж саме

(5.31)

Через зроблені припущення всі функції витрат 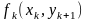є увігнутими (як суми увігнутої і лінійної функцій). Дана властивість значно спрощує процес рішення, оскільки для пошуку мінімуму увігнутих функцій досить розглянути тільки дві крайні точки множини, на якій відшукується мінімум. З урахуванням введеного позначення завдання (5.24)~(5.25) можна записати у вигляді:

(5.32)

при умовах

(5.33)

Розглянемо процедуру вирішення (5.32)-(5.33). Так як знаходиться мінімум суми ввігнутих функцій f_k(x_k, y_k+l), то відповідь буде досягатися на одній із крайніх точок множини, що визначається умовами (5.33). загальне число змінних x_k та у_к в системі (5.33) рівно 2 . Однак, враховуючи те, що в ній тільки рівнянь в оптимальному плані буде не більше ненульових компонент, причому для кожного періода k значення х_к та yk не можуть рівнятися нулю одночасно (в силу необхідності задоволення попиту або за рахунок замовлення, або за рахунок запа­су|). Формально це твердження|затвердження| можна представити|уявляти| у вигляді умови| доповнюючої нежорсткості:

(5.34)

де

(5.35)

З погляду змістовної інтерпретації умови (5.34) -(5.35) означають, що при оптимальному управлінні замовлення постачальникові на нову партію не повинне поступати, якщо на початку періоду є ненульовий запас, або розмір замовлення повинен дорівнювати величині попиту за ціле число періодів. Звідси витікає, що запас на кінець останнього періоду повинен дорівнювати нулю: . Останнє дозволяє вирішувати задачу в прямому напрямі, застосовуючи рекурентне співвідношення

(5.36)

Враховуючи (5.34) -(5.35) і угнутість укладаємо, що мінімум (5.36) досягається в одній з крайніх точок або , тому

(5.37)

тоді для попереднього періоду функція стану|достатку| може бути виражена|виказувати| як

(5.38)

на основі чого в загальному|спільному| вигляді|виді| отримуємо|одержуємо| модифіковану фор­му| для рекуррентного співвідношення

(5.39)

При подальших конкретизуючих припущеннях про вид функцій fk(xk, yk+l) можна отримати ще компактніші форми для рекурентних співвідношень. Проте ці питання носять достатньо приватний характер, і ми їх розглядати не будемо. Відзначимо лише, що приведені в даному пункті перетворення непогано ілюструють загальні підходи, вживані в динамічному програмуванні, а також ті властивості завдань, які відкривають можливості для ефективного і плідного використання відповідних методів.

Елементи випуклого аналізу

Якщо в деяких випадках класичні методи не дають результатів, то застосовуються чисельні методи, які являють собою обчислювальні процедури, поступово "поліпшуючі" значення цільової функції. Найбільш ефективні чисельні методи розроблені для завдань випуклого програмування (ЗВП), перевагою яких є те, що завжди мінімум (максимум) цільової функції існує і є абсолютним (глобальним). Ця властивість гарантує збіжність чисельних методів до правильного рішення.

Загальна постановка задачі випуклого програмування (ЗВП) має вигляд:

знайти: , (1)

при (2)

де f(x), g_і(x) — випуклі функції.

Функція f(x), визначена на деякій множині X, називається випуклою, якщо для будь-яких точок x₁ і х₂ з X і довільного числа λ: 0 < λ 1 виконується .

Зокрема, для функції одна змінної ця нерівність означає, що відрізок, що з'єднує довільну пару точок її графіка, ні в яких інших точках цей графік не перетинає.

Наприклад, функція f(x)=x² є випуклою на всій числовій осі, а функція f(x)=sіn(x) випукла на проміжку [π,2 π].

Якщо функція f(x) — випукла, то обернена до неї -f(x) — увігнута.

Множина X називається випуклою, якщо для будь-яких її точок х₁ і х₂ і довільного числа k : 0 k < 1 точка у=kх₁ + (1-k) х₂ також належать цій множині. Оскільки при будь-яких значеннях k у пробігає всі точки відрізка, що з'єднує точки х₁ і х₂ , то випуклою буде та множина, у якого будь-які дві крапки можна з'єднати відрізком, що повністю належить цій множині.

Якщо функція g(х) — випукла, то множина W, задана нерівністю g(х) 0, є випуклою.

Перетин випуклих множин, заданий системою обмежень виду W={x: g_i(х) 0, i=1,2,...,m), де всі функції g,(х) — випуклі, є випуклою множиною.

Чисельні методи рішення ЗВП дозволяють із будь-якої точки припустимої області наблизитися до шуканого рішення. Оскільки на кожній ітерації проводяться однотипні дії, то застосування ЕОМ є особливо ефективним.

Якщо ЗВП не має обмежень, тобто відсутні умови (2), то пошук экстремума функції f(x) ведеться на всьому просторі Rⁿ (нагадаємо, що при n=1 R — це числова вісь, при n=2 — це площина i т.д.).

Вдало вибираючи напрямок руху, можна з достатньою точністю прийти до екстремальної точки за скінченне число кроків (ітерацій). Зокрема, для диференційованої функції градієнт вказує напрямок найбільшого зростання функції, а антиградієнт — напрямок спадання функції. Якщо цільова функція f(x) має й другі похідні, то напрямок руху можна уточнити за допомогою матриці Гессе. Для недиференційовних функцій перспективні напрямки вибираються серед напрямків координатних осей або напрямків, отриманих випадковим чином.

Наявність обмежень істотно ускладнює методи рішення ЗНЛП. Для того, щоб обчислювальні процедури не виводили за межі допустимої області, потрібне рішення допоміжних завдань. Наприклад, якщо напрямок градієнта (антиградієнта) є неприпустимим (виходить за межі припустимої області), то потрібна операція проектування градієнта на припустиму область, а це досить складне завдання особливо при нелінійних обмеженнях (метод проекції градієнта).

Якщо пошук ведеться в деяких можливих напрямках, що не виходять за межі області, то для вибору найкращих серед них, потрібне рішення допоміжної задачі лінійного програмування (метод можливих напрямків - Зойтендейка).

Ідея методів штрафних і бар'єрних функцій полягає у відомості ЗНЛП із обмеженнями до ЗНЛП без обмежень, оскільки останні вирішуються порівняно просто. При цьому обмеження вихідної задачі спеціальним чином включаються до складу цільової функції нової задачі (задачі без обмежень).

ДИНАМІЧНЕ ПРОГРАМУВАННЯ

Часто виникають ситуації, коли рішення треба прийняти не відразу, а в кілька прийомів - крок за кроком. У таких випадках допомагає апарат динамічного програмування.

Одна з типових задач - це задача розподілу капітальних вкладень, коли на кожному етапі (наприклад, щорічно) вирішується задача розподілу. Потрібно встановити такий розподіл капітальних ресурсів на кожному етапі, при якому сумарний прибуток за всі етапи буде максимальною.

Рішення задач динамічного програмування базується на використанні принципу оптимальності: якщо деяка послідовність рішень оптимальна, то окремі наступні рішення всередині її оптимальні стосовно попередніх рішень. Відповідно до цього принципу задачу вирішують із останнього етапу. Потім переходять до рішення попереднього етапу, при цьому, природньо, відкидають ті можливі альтернативи, які суперечать уже відпрацьованому рішенню.

Перші завдання, які привели до появи методу, були динамічними задачами управління запасами.

Загальні відомості

Задача управління запасами (ЗУЗ) становлять один з найбільш численних класів економічних завдань ІСО. Правильне й своєчасне визначення оптимальної стратегії управління запасами, а також нормативного рівня запасів, дозволяє вівільнити значні оборотні кошти, заморожені у вигляді запасів, що, в остаточному підсумку, підвищує ефективність використовуваних ресурсів.

Основні характеристики моделей завдань УЗ

Елементами задачі УЗ є:

1) система постачання; 2) попит на предмети постачання; 3) можливість поповнення запасів; 4) функції витрат; 5) обмеження; 6) прийнята стратегія управління запасами.

Розглянемо детальніше кожний з елементів.

Системи постачання бувають : децентралізовані (однокаскадні) і централізовані (багатокаскадные).

Попит на предмети постачання може бути: стаціонарний або нестаціонарний; детермінований або випадковий.

Розрізняють способи поповнення запасів: миттєва поставка; затримка поставок на фіксований інтервал часу; затримка поставок на випадковий інтервал часу.

Функції витрат становлять в сукупності критерій ефективності прийнятої стратегії управління запасами й враховують витрати на зберігання, вартість поставок, витрати, пов'язані із замовленням кожної нової партії, витрати на штрафи.

Приведемо можливі варіанти складові функції витрат.

Витрати на зберігання бувають : пропорційні середньому рівню позитивного запасу за період часу існування позитивного запасу; пропорційні залишку до кінця періоду.

Вартість поставки буває: пропорційною обсягу поставки; постійною; пропорційною числу номенклатур; пропорційною необхідному приросту інтенсивності виробництва.

Штрафи бувають таких видів: пропорційні середній позитивній недостачі за період; пропорційні позитивній недостачі до кінця періоду; постійні; нелінійні функції від середньої недостачі й тривалості її існування.

Обмеження в ЗУЗ накладаються: на максимальний обсяг запасів; максимальну вагу; максимальну вартість; середню вартість; число поставок у заданому інтервалі часу; обсяг поставки; імовірність недостачі.

Формально задача динамічного програмування має вигляд:

Знайти max Z =

при умовах a_j>0, x_j 0.

Цільова функція задачі є сумою функцій від однієї змінної. Така функція називається аддитивною. Якщо всі f_і(х_і), i=1,n, — випуклі (увігнуті), то для рішення може бути застосований метод множників Лагранжа. Однак, якщо є багато локальних максимумів, то цей метод дає лише одне з таких рішень. У випадку, якщо потрібно знайти глобальний максимум, використається наступний метод.

Передбачається, що всі {а_j), j=1,...,n I b — цілі числа, а змінні {x_j} можуть приймати тільки цілочисельні значення.

Приклад задача динамічного програмування. Є х — кількість капітальних вкладень, які необхідно розподілити між двома галузями. Кількість капітальних засобів у, вкладене в першу галузь, за рік приносить прибуток g(у) = 0,8y. Частка капітальних засобів x-y, вкладених у другу галузь, приносить за рік доход h(x-y) =0,5(x-y). Під кінець року засоби, вкладені в першу галузь, складуть а(у) = 0,3у, а для другої галузі ця величина складе b(x-y) = 0,6(x-y). Після закінчення кожного року капітальні вкладення, що залишилися, заново розподіляються між галузями. Необхідно встановити розподіл таким чином, щоб сумарний прибуток за три роки був максимальним.

Отже, спочатку шукають величину у₂ — кількість засобів, вкладених у третій рік, потім y₁ й у₀ (відповідно для другого й першого років). Відповідно до принципу оптимальності, незалежно від величин у₁ та у₀, а також х₂ — кількість ресурсів, отриманих до початку третього етапу, необхідно щонайкраще використати доступну кількість ресурсів, тобто вирішити задачу

0 у₂ х₂

або

.

0 у₂ х₂ 0 у₂ х₂

Очевидно, max можливий при х₂=у₂.

Отже, всі ресурси на останньому етапі потрібно направити в першу галузь. При цьому буде отриманий прибуток f₁ (х₂)=0,8х₂.

Тепер знайдемо у₁. Розглянемо двокроковий процес - останній і передостанній етапи.

Необхідно щонайкраще використати ресурси х₁ , не цікавлячись попереднім рішенням. Максимальний сумарний доход за останні два етапи буде рівний

.

0 у₁ х₁

Тут — прибуток на передостанньому етапі при y₁, a — максимальний прибуток на останньому етапі при тій же умові.

Необхідно вибрати y₁ [0,х₁] таке, щоб у дужках одержати максимум.

По відомому f₁ отримуємо

0 у₁ х₁

0 у₁ х₁

_.

0 у₁ х₁

Звідси f(x₁)=1,04x₁ та y₁=x₁.

Виходить, на передостанньому етапі також всі капітальні вкладення повинні бути спрямовані в першу галузь.

Аналогічно, для першого етапу

0 у₀ х₀

0 у₀ х₀

0 у₀ х₀

Тут максимум досягається при у = 0. Отже, найбільший сумарний доход за всі етапи складе f₃(x)= 1,124.

На першому етапі всі ресурси необхідно направити в другу галузь: у = 0.

Значить: Оптимальна стратегія

Уо=0, y₁=х₁, у₂=х₂.

I етап: всі ресурси — у другу галузь і прибуток становитиме h(x) = 0,5x.

Залишиться під кінець року b(х) — 0,6х капітальних вкладень, які будуть спрямовані в першу галузь і дадуть прибуток g(0,6х) =0,8*0,6х =0,48х.

Залишок ресурсів при цьому складе а(0,6х) = 0,3*0,6х = 0,18х.

Прибуток на третьому етапі: g(0,18х) =0,8*0,18х =0,144х,

А сумарній прибуток рівний 0,5х+0,48х+0,144х=1,124х

Продемонструємо процес рішення завдання в наймі робітників на конкретному прикладі:

Для функціонування деякого підприємства протягом чотирьох місяців (пронумерованих від 1 до 4) по нормах потрібні наступні кількості працівників однакової кваліфікації,:

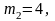
причому перед початком першого місяця (у нульовому місяці) фактично є співробітника. Адміністрація планує наприкінці кожного місяця k (крім останнього) коректувати число працюючих на величину x_k, , х₄=0. На прийом одного співробітника необхідно затратити 9 у.е., а на звільнення - 6 у.е. Передбачається, що витрати на утримання надлишкового працівника становлять 8 у.е., а у випадку недостачі персоналу доводиться нести витрати в розмірі 12 у.е. за кожне вакантне місце.

Потрібно знайти оптимальні значення збільшення чисельності працюючих наприкінці кожного з перших трьох місяців, при яких сумарні витрати за весь розглянутий період будуть мінімальними.

На початку рішення запишемо в аналітичній формі функції витрат на прийом-звільнення співробітників (и), а також на утримання ненормативного штату (g). Із цією метою введемо функції

Оцінки ефективності керування на кожному кроці приймають вигляд:

Оскільки в поставленому завданні задана початкова умова , її рішення починається з кінця, і, отже, будуть застосовуватися рекурентні співвідношення (5.17). З технічної точки зору буде зручно на кожному кроці складати дві таблиці значень: функції витрат, одержаних починаючи з поточного кроку в залежності від поточного стану й керування,

( 5-22)

і функції мінімальних витрат у залежності від поточного стану

(5-23)

Для скорочення обсягу табличних значень можна скористатися властивістю випуклості функції , що випливає з випуклості l і g. З випуклості функції слідує, що заповнювати таблицю її значень необхідно лише до тих пір, поки вони зменшуються, тобто можна зупинитися, як тільки чергове значення виявляється більше попереднього. Відзначимо, що подібні прийоми дуже широко використовуються в динамічному програмуванні. Зрозуміло, ілюстровані методи не розраховані на ручний рахунок, оскільки пов'язані з дуже більшим обсягом рутинних обчислень. Заради стислості нижче наведені тільки фрагменти таблиць, що містять значення, що нас цікавлять.

Ітерація 1. Візьмемо, що k = 4. На даному етапі функція стану 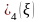може бути знайдена безпосередньо, якщо врахувати, що =0 і и(0) = 0:

Таблиця значень даної функції й умовні оптимальні керування мають вигляд

	0	1	2	3	4	5	6
	24	12	0	8	16	24	32
	0	0	0	0	0	0	0

Ітерація 2. Приймаємо, що k = 3 . Попередньо заповнимо таблицю значень функції для досить великої кількості аргументів відповідно до формули:

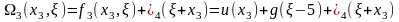
	0			1			2
	1	2	3	0	1	2	-1	0	1
	69	78	87	48	57	66	42	36	45
	12	0	8	12	0	8	12	0	8
	81	78	95	60	57	74	54	36	53
	3			4			5
	-2	-1	0	-3	-2	-1	-4	-3	-2
	36	30	24	30	24	18	24	18	12
	12	0	8	12	0	8	12	0	8
	48	30	32	42	24	26	36	18	20

Вибираючи мінімальні по х₃ значення , складемо таблицю і відповідні значення умовних оптимальних управлінь :

	0	1	2	3	4	5
	78	57	36	30	24	18
	2	1	0	-1	-2	-3

Ітерація 3. Приймемо, що k = 2 . Так само, як на попередній ітерації, заповнимо таблицю значень функції відповідно до формули:

	0			1				2
	1	2	3		0	1	2		-1	0	1
	57	66	75		36	45	54		30	24	33
	57	36	30		57	36	30		57	36	30
	114	102	105		93	81	84		87	60	63
	3			4				5
	-1	0	1		-1	0	1		-1	0	1
	18	12	21		6	0	9		14	8	17
	36	30	24		30	24	18		24	18	32
	54	42	45		36	24	27		38	26	49

Вибираючи мінімальні по х₂ значення , складемо таблицю і відповідні значення умовних оптимальних керувань :

	0	1	2	3	4	5
	102	81	60	42	24	26
	2	1	0	0	0	0

Ітерація 4. Приймаємо, що k = 1. Аналогічно попередньому, заповнимо таблицю значень функції відповідно до формули:

	0			1			2
	3	4	5	2	3	4	1	2	3
	63	72	81	42	51	60	21	30	39
	42	24	26	42	24	26	42	24	26
	105	96	107	84	75	86	63	54	65
	3			4
	0	1	2	-1	0	1
	0	9	18	14	8	17
	42	24	26	42	24	26
	42	33	44	56	32	43

Вибираючи мінімальні по х₁ значення , складемо таблицю і відповідні значення умовних оптимальних керувань :

	0	1	2	3	4
	96	75	54	33	32
	4	3	2	1	0

Ітерація 5. На останній ітерації, у зв'язку з наявністю початкової умови , досить обчислити

і знайти як точку мінімуму . Прості обчислення показують, що мінімум

досягається при (2) = 1.

Отже, , після чого зворотним ходом послідовно обчислюються оптимальні керування й оптимальні стани (оптимальна траєкторія):

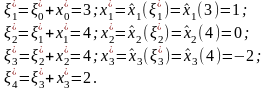
Отже, результати розрахунку свідчать, що при заданій системі розцінок у третьому місяці вигідніше не брати 5-го працівника, а компенсувати його відсутність додатковими виплатами за наднормову роботу присутніх співробітників.

Лінійне програмування

При рішенні ряду технологічних задач вираз для критерію оптимальності може бути представлено у вигляді лінійної функції від вхідних в нього оптимізаційних змінних . При цьому на ці змінні можуть бути покладені певні обмежуючі умови також у формі лінійних рівностей і нерівностей. В цьому випадку рішення оптимізаційних задач здійснюється за допомогою методу лінійного програмування.

Вираз для цільової функції в загальному вигляді може бути представлений так ;

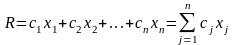(j=1,2,…n), (2.10)

Де - задані постійні коефіцієнти.

Вираз (2,10) називається лінійною формою . На вибір оптимальних значень змінних накладаються допоміжні умови , які встановлюють зв'язок між оптимізуючими змінними (вони можуть включати в себе як рівність, так і нерівність):

(2,11)

Коефіцієнти в (2,10) і 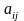у виразі (2,11) являються дійсними числами і можуть позитивними та негативними, серед них можуть бути і рівні нулю. Число обмеженого типу рівнянь не повинно перевищувати загального числа оптимізуючих змінних в лінійній формі . Число нерівностей може бути будь-яким .

В задачах лінійного програмування пропонують, що оптимізуючі змінні позитивні,

>0, j=1,2,….n. Також вважають , що всі величини у виразі (2,11) відрізняються від нуля і позитивні . Якщо якесь значення буде позитивним , то, перемножуючи ліву і праву частини відповідного рівняння на -1 , його приводять до вигляду, коли права частина приймає позитивне значення . Якщо якесь значення буде дорівнювати нулю, то в ліву і праву частини відповідного виразу (2,11) добавимо доданок , що робить величину більшою від нуля . При цьому вважають що добавлений доданок увійшов лінійну форму (2,10) , але з нульовим коефіцієнтом , що не змінило вираз для цільової функції .

Для скорочення виразу (2,11) може бути представлено у вигляді…

, і=1,2,…m, j=1,2,….n (2,11а)

Оптимальним рішенням задачі лінійного програмування являється така сукупність значень незалежних змінних, яка відповідає умовам (2,11) і забезпечує , в залежності від постановки задачі , максимальне і мінімальне значення лінійної форми.

Вважають, що оптимум досягається при максимальному значенні лінійної форми . Випадок, коли необхідно знайти мінімальне значення лінійної форми , може бути приведено до задачі максимізації шляхом зміни знаків у всіх коефіцієнтах ( j=1,2,…n).

Нехай необхідно знайти розв’язок задачі максимізації критерію оптимальності , який має наступний вигляд

Розглядається вираз в якому n=2, c1=1, x1,x2 тип рівності

(б)

Та нерівність

(в)

У виразі (б) згідно (2,11)

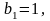
Так як нерівність розглянутої задачі дорівнює двом , процес рішення може бути представлений графічно . Рівності (б) на фазній поверхні змінних х1 та х2 визначають область можливих значень цих змінних , яка знаходиться в першому квадранті і обмежена лініями , відповідним рівнянням

На малюнку 2,10 лінії, обмежуючі розглянуту область Х , заштриховані з зовнішньої сторони .

У відповідності зі структурою лінійної форми (2,10) та (а) похідні від критерію оптимальності по оптимізуючи змінним постійні, неперервні та не перетворюються в області Х в нуль:

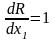
Це означає , що екстремум цільової функції може бути досягнутий тільки на границі області Х . Величина критерію оптимальності має постійне значення на протязі лінії L , яка знаходиться за рівнянням

На рис(2,10) ця лінія зображена для значення l=0,4. Якщо її переміщувати на площині ( ) паралельно самій собі в напрямку , указаною стрілкою , то значення l, а відповідно, і величина цільової функції будуть збільшуватись.

Очевидно, що максимальному значенню R в розглянутому випадку відповідає певне положення лінії l в області Х , коли вона проходить через точку К, яка являється вершиною багатокутника , обмеженого лініями (б) та (в). Максимальне значення цільової функції визначається координатами точки К , які можуть бути визначені сумісним рішенням рівнянь (б) :

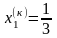
Підставивши отримані значення оптимізуючи змінних (д) в рівнянні лінійної форми (а) дозволяє визначити максимальне значення цільової функції

В розглянутому прикладі максимальне значення цільової функції забезпечується при певних кінцевих значеннях оптимізуючих змінних. Але в задачах лінійного програмування бувають випадки, коли рішення задачі відповідає безкінечний набір значень оптимізуючих змінних. Геометрично це відповідає варіанту , коли одна з границь багатокутника області можливих змінення змінних паралельна лінії l, визначеної виразом критерію оптимальності.

Якщо для умови попереднього прикладу при обмеженнях + =1, + =1, 0, 0 цільова функція буде мати вигляд R = + , то максимум функції буде мати місце по лінії АК (див. мал. 2.10). В цьому випадку рівняння для лінії l має вигляд

l = + = 0,4. Оскільки обмеження типу рівність залишилися незмінними, значення 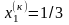та також не змінилися, максимальне значення цільової функції буде , причому це значення цільової функції може бути досягнуто при всіляких поєднаннях та , які задовольняють відрізок АК.

У розглянутому прикладі система обмежень описує замкнуту область можливих значень оптимізуючих змінних. Інколи система обмежень може визначити і незамкнену область. Так, якщо обмеження описуються виразами , , 0, 0 (мал. 2.11), то цільова функція виду досягне максимуму при нескінченно великих значеннях та , так як можливості переміщення лінії l = + (l = 0,25) у напрямку збільшення R не обмежені.

В той же час, при незамкненій області зміни змінних максимум цільової функції може лежати і не у нескінченності. Якщо при перерахованих вище обмеженнях цільова функція має вигляд R = , то переміщення лінії l обмежено. Розв’язуючи систему рівнянь , можна обчислити значення , та визначити максимальне значення цільової функції

В загальному випадку випадкового числа п оптимізуючих змінних геометрична інтерпретація задачі неможлива. Область допустимих значень змінних у п – мірному просторі являється багатогранником, обмеженим гіперплощиною, зрівнювання яких задаються обмеженнями (2.11); Поверхня, вздовж якої критерій оптимальності має постійне значення, буде представляти собою також гіперплощиною, яка визначається конкретним видом виразів (2.10).