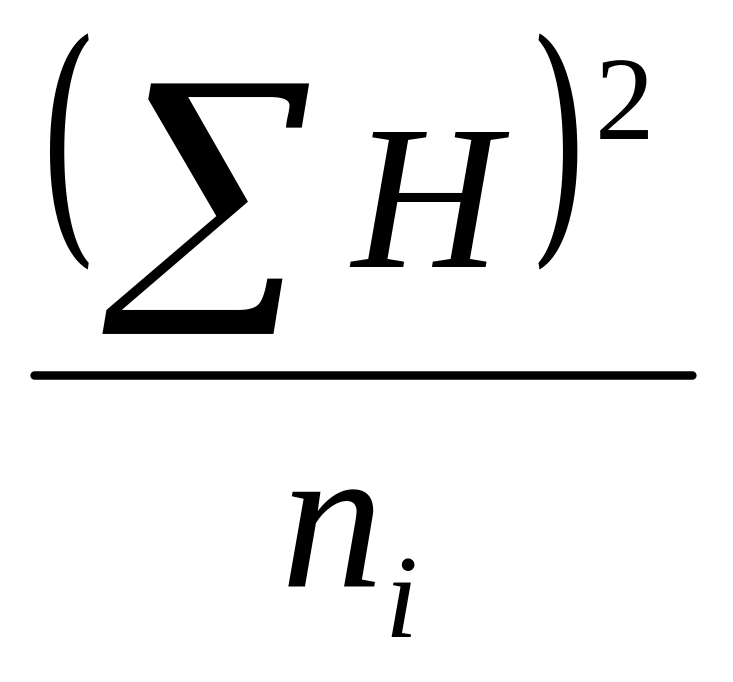Числа степеней свободы для разных источников варьирования
Источник варьирования |
Алгоритм вычисления числа степеней свободы |
Вычисление числа степеней свободы |
Число |
общая |
ky = a × r × n – 1 |
ky = 6×3×10 – 1 = |
= 179 |
гибриды |
ka = a – 1 |
ka = 6 – 1 = |
= 5 |
повторности |
kr = r – 1 |
kr = 3 – 1 = |
= 2 |
Взаимодействие гибридов и повторностей |
kar = (a – 1) × (r – 1) |
kar = (6 – 1)×(3 – 1) = |
= 10 |
Остаток или ошибки, или случайная дисперсия: неисправленная величина (m=kz) |
kz = ky – ka – kr – kar = (a × r × n – 1) – (a – 1) – (r – 1) – ((a – 1) × (r – 1)) = a×r×n – 1 – a + 1 – r + 1 – (a×r – r – a + 1) = a×r×n – a – r + 1 – a×r + r + a – 1 = a×r×n – a×r = a×r×(n – 1) или, что тоже самое kz = N – a × r = a×r×n – a × r = a×r×(n – 1) |
kz = 6×3×(10 – 1) = |
= 162 |
OKC |
kOKC = p – 1 |
kOKC = 4 – 1 = |
= 3 |
CKC |
kCKC = [p × (p – 3)]/2 |
kCKC = [4×(4 – 3)]/2 = |
= 2 |
Исправленная |
kе = kz × r × n |
kе = 162 × 3 × 10 = |
=4860 |
В таблице при определении числа степеней свободы остаточной (или средовой или случайной или экотипической) изменчивости исходим из представления о числе степеней свободы остаточной дисперсии как о разности между общим числом степеней свободы и степенями свободы всех организованных факторов (Гужов, Фукс, Валичек, 1991, стр. 334; Доспехов, 1973, стр. 167 – 168; Лакин, 1980, стр. 219, 221, 233).
Примечание
Предложенная схема расчетов имеет свои методические ограничения в части вычисления величины специфической комбинационной способности. В частности, число комбинаций скрещивания не может быть меньше 3. В противном случае число степеней свободы для СКС становится равным «0», что бессмысленно и делает деление на такую степень свободы невозможным, или будет отрицательным, что также бессмысленно.
a×b×(c – 1)×b×c = (a×b×c – a×b) × b×c =
(a – 1) × (r – 1) × n = (a×r – r – a +1) × n = a×r×n – r×n – a×n + n = a×r×n – (r×n + a×n) + n = a×r×n – n×(r + a) + n = a×r×n – n×(r + a) – 1)
Таблица ***
Дисперсионный анализ высоты 20-летних гибридов дуба
Крите-рии |
Варианты опыта - Гибридные комбинации (а) а=6 Фактор высшей иерархии |
Сум-ма |
|||||||||||||||||
а1 (1х2) |
а2 (1х3) |
а3 (1х4) |
а4 (2х3) |
а5 (2х4) |
а6 (3х4) |
||||||||||||||
Повторности испытания потомства (r=3) в каждой комбинации скрещивания Фактор низшей иерархии |
|||||||||||||||||||
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
||
Hi |
5,5 |
5,9 |
6,4 |
6,5 |
6,0 |
6,3 |
3,0 |
3,5 |
4,0 |
3,1 |
4,1 |
3,9 |
2,5 |
4,1 |
4,0 |
3,5 |
4,1 |
2,8 |
|
5,4 |
6,1 |
6,0 |
6,5 |
5,9 |
6,1 |
3,4 |
3,4 |
4,1 |
3,0 |
3,0 |
3,9 |
4,1 |
2,6 |
4,1 |
3,5 |
4,0 |
2,9 |
||
6,0 |
6,1 |
6,2 |
6,1 |
5,8 |
5,4 |
2,8 |
3,4 |
3,2 |
2,8 |
3,6 |
3,6 |
4,1 |
4,1 |
4,1 |
3,8 |
4,0 |
4,9 |
||
6,2 |
6,3 |
5,8 |
5,5 |
6,3 |
5,0 |
3,2 |
3,2 |
3,1 |
2,6 |
3,4 |
3,5 |
3,9 |
3,9 |
4,0 |
3,5 |
4,1 |
4,1 |
||
6,1 |
5,8 |
5,9 |
5,4 |
6,5 |
6,5 |
3,0 |
2,8 |
2,5 |
3,4 |
2,8 |
3,5 |
3,5 |
3,6 |
4,9 |
2,8 |
4,0 |
4,0 |
||
6,4 |
5,7 |
5,7 |
4,9 |
5,2 |
6,3 |
3,0 |
2,8 |
2,5 |
3,0 |
2,8 |
2,5 |
3,5 |
3,8 |
3,9 |
4,1 |
3,9 |
3,8 |
||
6,1 |
5,1 |
5,0 |
6,1 |
6,3 |
6,0 |
2,9 |
2,0 |
3,8 |
2,5 |
2,9 |
3,4 |
3,9 |
3,8 |
3,9 |
4,1 |
3,9 |
3,8 |
||
6,0 |
6,4 |
6,0 |
6,3 |
6,2 |
5,9 |
2,8 |
4,1 |
2,1 |
2,1 |
3,1 |
3,8 |
4,0 |
4,1 |
3,8 |
4,0 |
3,2 |
3,8 |
||
5,9 |
6,0 |
6,2 |
6,4 |
6,1 |
5,8 |
3,6 |
4,1 |
3,0 |
2,9 |
3,2 |
4,0 |
4,9 |
3,6 |
3,5 |
2,9 |
3,1 |
3,4 |
||
6,0 |
6,1 |
6,3 |
6,3 |
6,1 |
5,6 |
3,4 |
2,1 |
3,1 |
3,1 |
3,4 |
4,0 |
2,6 |
3,8 |
3,5 |
3,9 |
2,9 |
3,0 |
||
|
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
10 |
N=180 |
|
59,6 |
59,5 |
59,5 |
60 |
60,4 |
58,9 |
31,1 |
31,4 |
31,4 |
28,5 |
32,3 |
36,1 |
37 |
37,4 |
39,7 |
36,1 |
37,2 |
36,5 |
ΣΣHi= 772,6 |
|
356,04 |
355,23 |
355,47 |
362,68 |
365,98 |
348,81 |
97,41 |
103,32 |
102,62 |
82,45 |
105,83 |
132,13 |
141,56 |
141,64 |
158,99 |
132,27 |
140,3 |
136,95 |
ΣΣH2i=3615,81 |
|
355,22 |
354,03 |
354,03 |
360,00 |
364,82 |
346,92 |
96,721 |
98,596 |
98,596 |
81,225 |
104,33 |
130,32 |
136,9 |
139,88 |
157,61 |
130,32 |
138,38 |
133,23 |
(ΣHi)2 Σ-------- ni 3595,60 |
|
5,96 |
5,95 |
5,95 |
6 |
6,04 |
5,89 |
3,11 |
3,14 |
3,14 |
2,85 |
3,23 |
3,61 |
3,7 |
3,74 |
3,97 |
3,61 |
3,72 |
3,65 |
ΣHi Σ-------- ni = 77,51 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение задачи состоит из трех этапов.
доказательство существенности различий между гибридными комбинациями.
доказательство наличия эффектов комбинационной способности.
анализа комбинационной способности отдельных родителей и вариантов скрещивания.