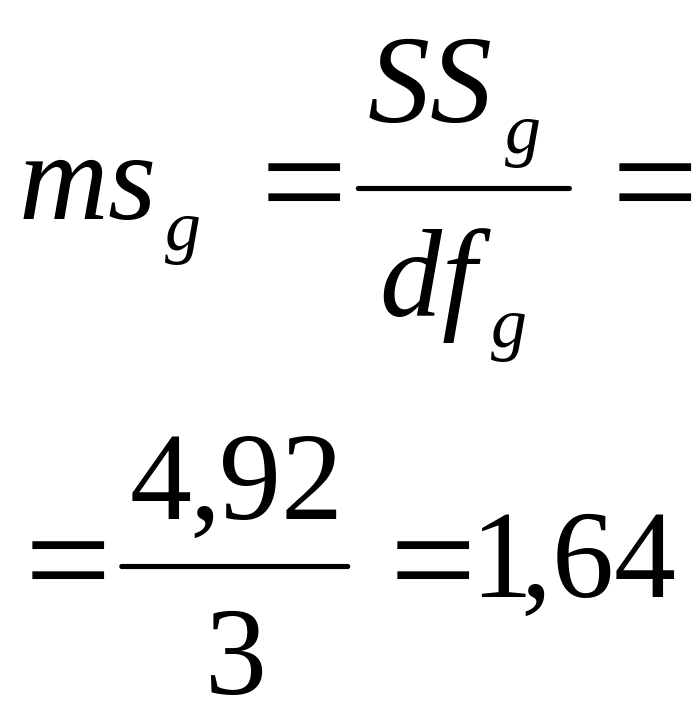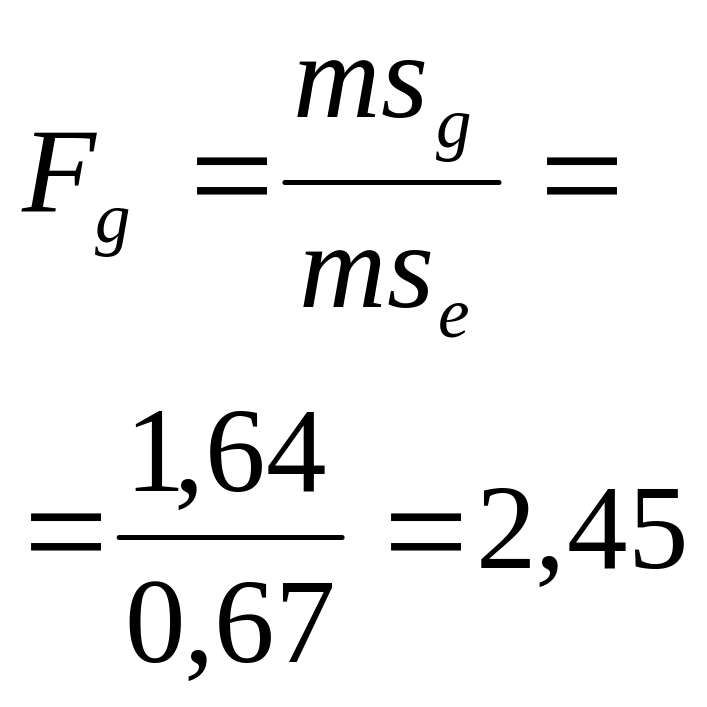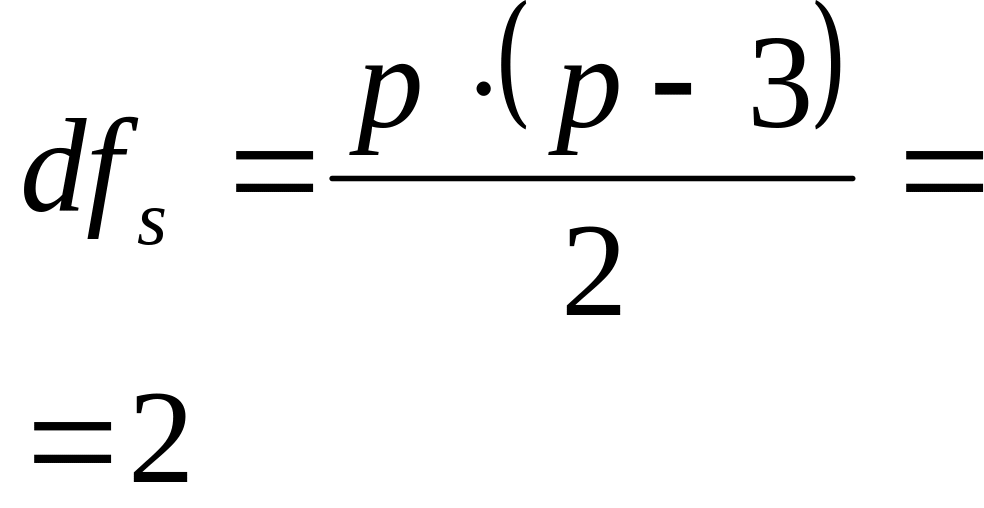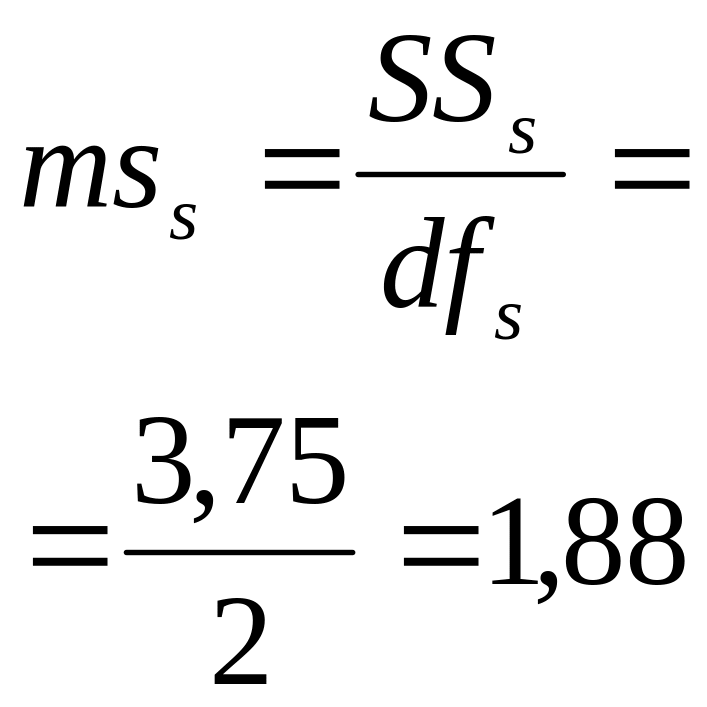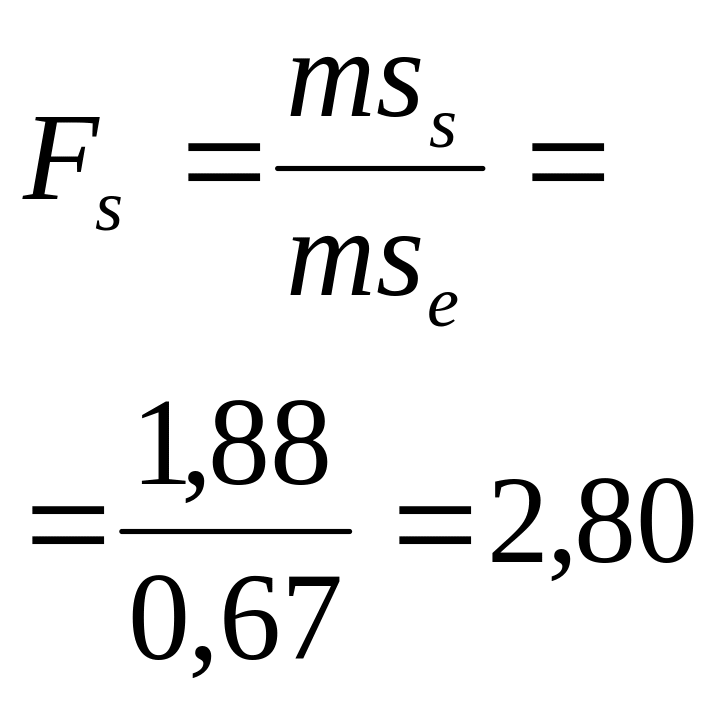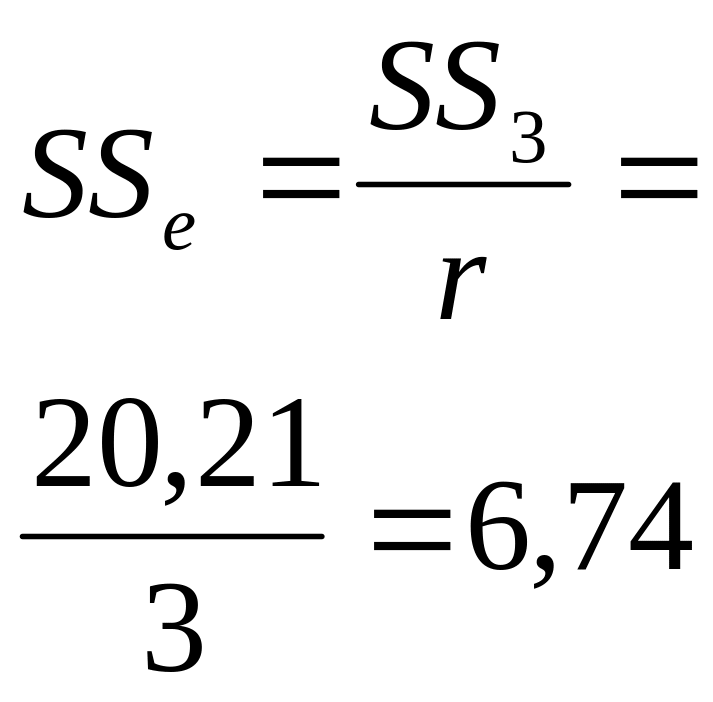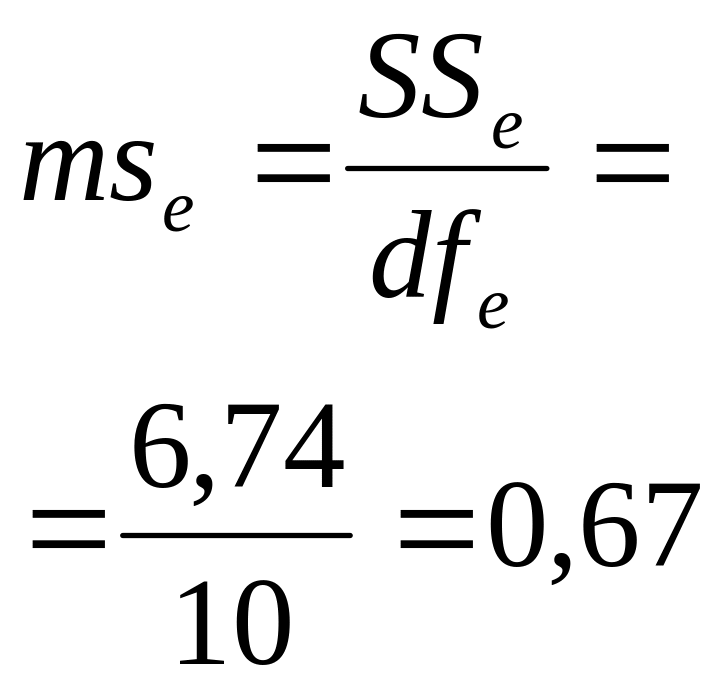2 Этап.

1. Вычисляются средние высоты гибридов по вариантам скрещивания, включая все повторности. Результаты заносятся в диаллельную таблицу (табл. ****).

ВНИМАНИЕ!

В учебнике М.М. Котова (1997) не объясняется порядок заполнения таблицы!

При этом заполнение таблицы осуществляется так, что нижняя треугольная часть таблицы является соответствующим повторением её верхней треугольной части. В этом случае принимается во внимание тот факт, что обратных скрещиваний и самоопыления не проводилось. Тогда (!) в нижней треугольной части (!) будем иметь значения признака гибридного потомства, у которого номер материнского дерева является номером отцовского дерева, а номер отцовского – соответственно номером материнского.

Здесь уместнее было бы указать не номера отцовских и материнских деревьев, а «номера особей в прямых диаллельных скрещиваниях». Тогда становится понятным, что нижняя треугольная часть является соответствующим повторением (поскольку повторяются те же комбинации прямых скрещиваний) верхней треугольной части таблицы.

Таблица ****

Номера отцовских деревьев	Номера материнских деревьев
	1	2	3	4
1	-	5,95	5,98	3,15	15,08
2	5,95	-	3,24	3,84	13,03
3	5,98	3,24	-	3,66	12,88
4	3,15	3,84	3,66	-	10,65

2. Находим общую полусумму средних значений высот деревьев – сумму одной из частей (верхней или нижней) полученной равномерной прямоугольной матрицы (только верхняя треугольная часть или только нижняя треугольная часть), т.е. суму значений признака (в нашем случае высоты деревьев) у особей, являющихся гибридным потомством при односторонних прямых диалльльных скрещиваниях.

3. Подсчитываем суммы квадратов, обусловленные общей и специфической комбинационной способностью (SSg, SSs).

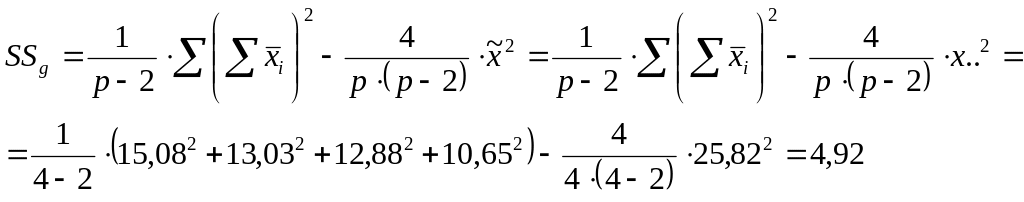
4. Подсчитываем суммы квадратов, обусловленные специфической комбинационной способностью (SSs):

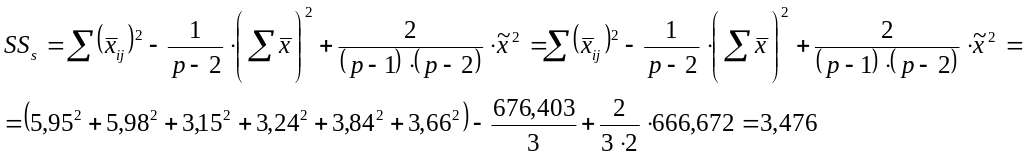
где:

р – число родительских пар.

5. Проводим дисперсионный анализ комбинационной способности (табл. ****):

Таблица ****

Дисперсионный анализ комбинационной способности

родительских деревьев дуба

№	Источники варьирования	Сумма квадратов отклонений SS	Число степеней свободы df	Средний квадрат отклонений ms	Критерий Фишера опытный Fфактич.
1.	Общая комбинационная способность	SSg=4,92	df = p – 1 = 3
2.	Специфическая комбинационная способность
3.	Случайные отклонения				-
	Стандартные значения F	Fg = 3,8 – 7,0 – 13,1 Fs = 4,1 – 7,9 – 14,9

Различия по общей и специфической комбинационной способности оказались недостоверными.

Если бы Fg был достоверен, можно было бы приступить к третьему этапу анализа.

3 этап.

Рассчитывается средний эффект (u) и эффекты общей комбинационной способности отдельных родителей (g_i).

1. Рассчитываем средний эффект:

ВНИМАНИЕ!

Здесь уместнее объяснить, что средний эффект по сути является общим средним значением селектируемого (анализируемого) признака, отклонение от которого частного среднего значения признака гибридного потомства отдельного дерева во всех комбинациях его скрещивания со всеми остальными особями есть мера оценки ОКС.

Тогда предложенный алгоритм расчета общего среднего уместнее представить в более развернутой форме:

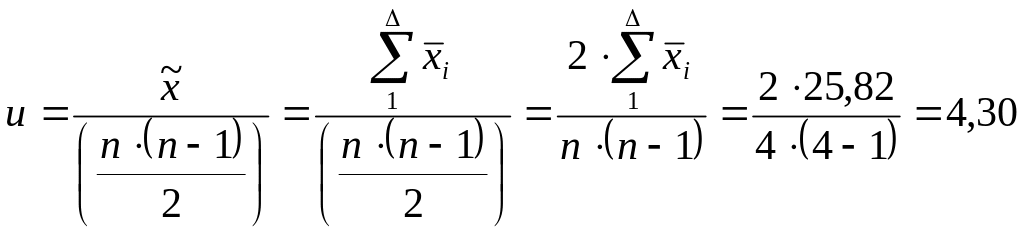, где

.

2. Рассчитываем эффекты общей комбинационной способности отдельных родителей:

ВНИМАНИЕ!

Возможно, приведен не точный алгоритм расчета.

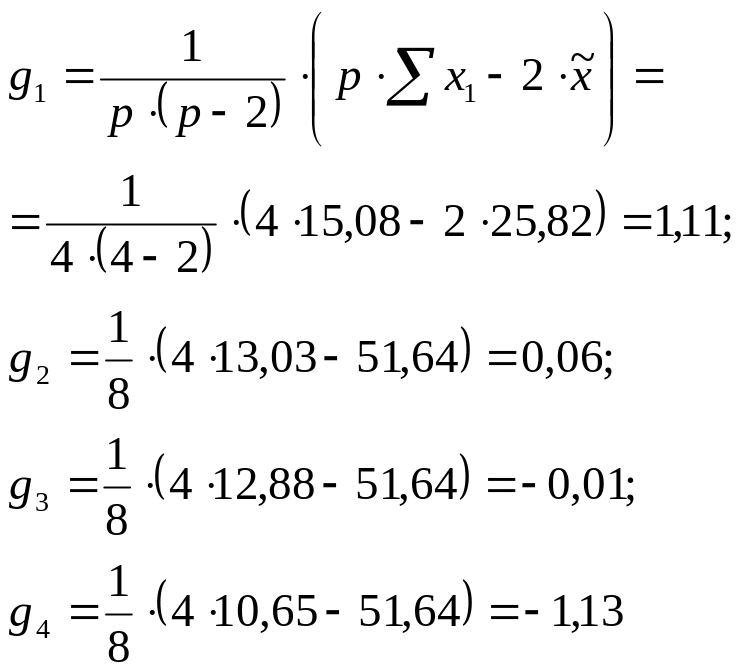
ВЫВОД.

Лучшей комбинационной способностью обладает первое дерево.

Сходный вывод напрашивается даже при общем знакомстве с исходными данными. В двух комбинациях из трех средняя высота гибридного потомства этого дерева почти в два раза превосходит высоту гибридных растений в других вариантах скрещивания.

ВНИМАНИЕ!

Скорее всего, более корректным будет алгоритм расчета, в котором при вычислении «средних» значений «контрольных» деревьев и полусибсового потомства, происходящего от одной особи и разных опылителей, в знаменателе первого сомножителя должна стоять разность между числом родительских пар и «единицей», а не «двойкой».

В этом случае ОКС каждого из родителей рассчитывается как разность между общим средним значение признака всех гибридов прямого диаллельного скрещивания во всех его комбинациях (когда растение выступает и как отцовское, и как материнское) и средним значение признака гибридного потомства одного из испытываемых родителей во всех комбинациях скрещивания, где одним (любым – материнским или отцовским) из родителей было испытываемое дерево.

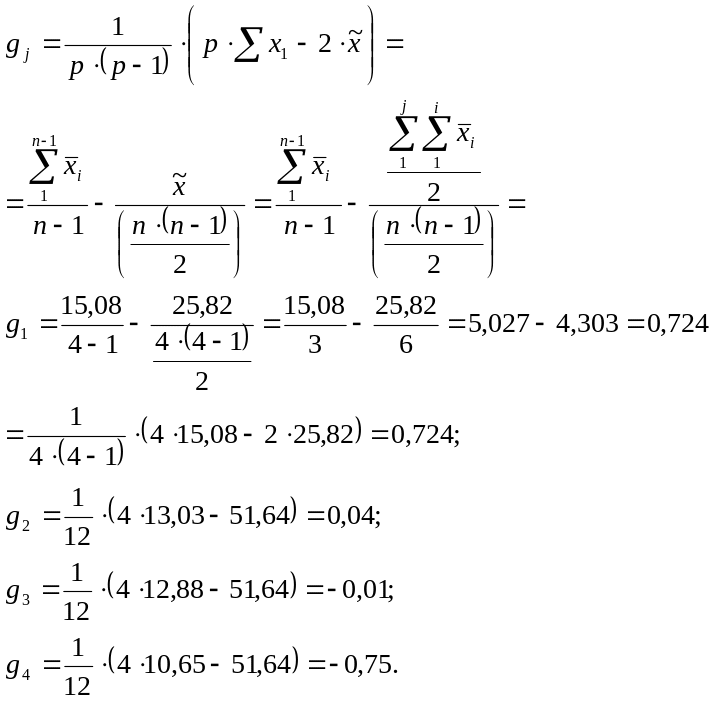
3. В случае достоверности ms_s далее вычисляются константы специфической комбинационной способности по формуле:

Для нашего примера получим:

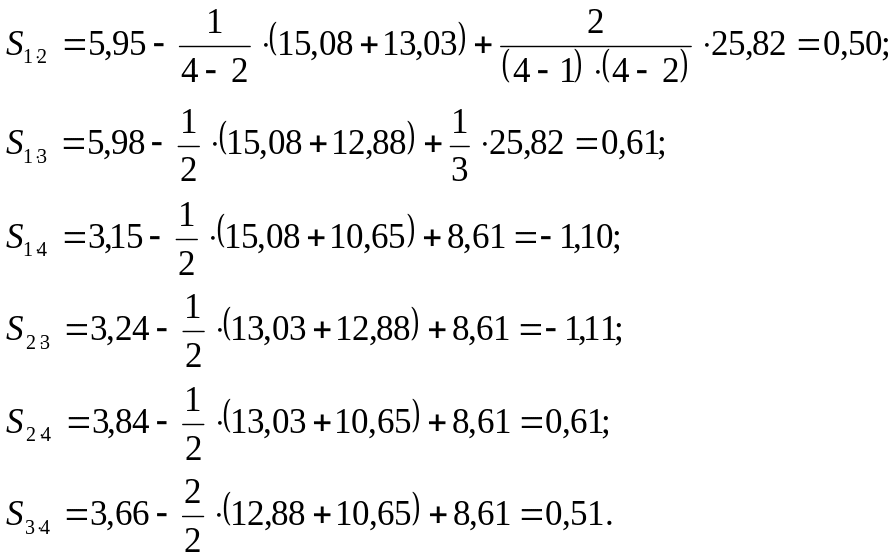
4. Полученные значения констант (S_ij) заносим в следующую таблицу (табл.*****):

Таблица ****

Эффекты общей (g_i), константы специфической (S_ij) и

вариансы специфической комбинационной способности ( )

Номера отцовских деревьев	Константы СКС по номерам материнских деревьев, Sij				Эффекты ОКС, gi	Вариансы СКС,
	1	2	3	4
1	-	0,50	0,61	-1,10	1,11	0,56
2	0,50	-	-1,11	0,61	0,06	0,60
3	0,61	-1,11	-	0,51	-0,01	0,60
4	-1,11	0,61	0,51	-	-1,13	0,59

5. Вычисляются вариансы специфической комбинационной способности по каждому дереву:

Скорректированный алгоритм:

σ²_Si =

По М.М. Котову (1997), запись несет в себе неточности, требующие коррекции, имеем:

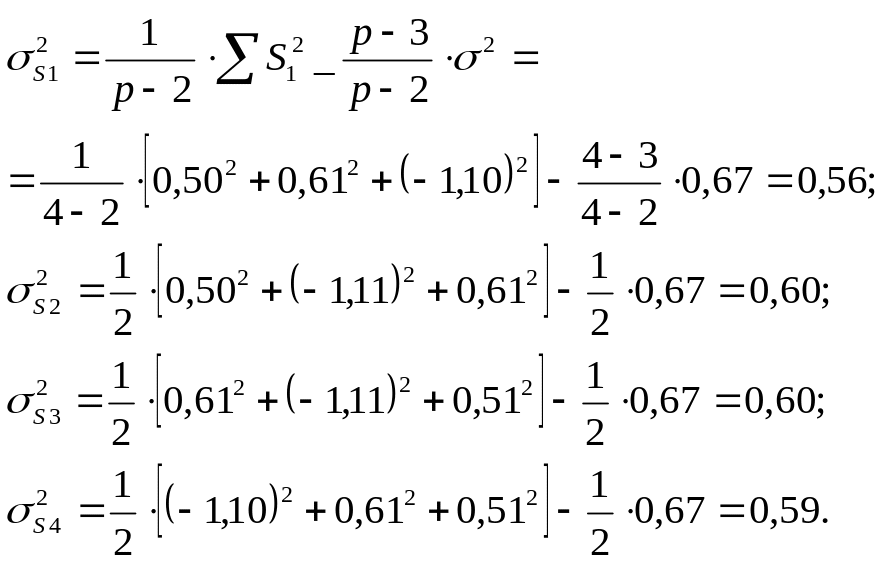
6. Значения варианс СКС по каждому дереву заносим в ту же таблицу (табл.***).

ВЫВОД.

По специфической комбинационной способности взятые для скрещивания деревья не отличаются друг от друга, на что и указывала раньше недостоверность ms_s.

Вопросы и задания для самопроверки и контроля знаний.

1. Сформулируйте определение понятия «комбинационная способность».

2. Какие показатели используются для оценки комбинационной способности?

3. В ходе каких испытаний устанавливается величина общей комбинационной способности?

4. В ходе каких испытаний устанавливается величина специфической комбинационной способности?

5. Оценкой чего является общая комбинационная способность?

6. Оценкой чего является специфическая комбинационная способность?

7. Какие методы изучения комбинационной способности разработаны Б. Гриффингом (1956)?

8. Какой из общеизвестных методов статистического анализа наиболее часто применяется при расчетах величины комбинационной способности?

ДУБЛИ:

- общую сумму всех значений признака полусибсовых групп: для полной реципрокной схемы диаллельных скрещиваний получим (Σx_i = Σ Σ x_ij) Σx_i = 2548,6;

- сумму квадратов сумм значений признака полусибсовых групп (Σx_i² = Σ[Σ x_ij]²)

- квадрат этой полусуммы (x..² = [1/2× Σ Σ x_ij]²), x..² = 1623840,49;

- её полусумму (x.. = 1/2× Σ Σ x_ij = Σ x_i), x.. = 1274,3;

- квадрат этой полусуммы (x..² = [1/2× Σ Σ x_ij]²), x..² = 1623840,49;

- общую сумму квадратов всех значений признака гибридов одностороннего скрещивания (только прямые скрещивания), равную полусумме квадратов значений признака всех гибридов полной схемы реципрокного диаллельного скрещивания (1/2×Σ Σ x²_ij.), 1/2×Σ Σ x²_ij. = 108405,73.

Общую комбинационную способность любой родительской формы (i) определяют по формуле: