§ 6. Непрерывность функций

6.1. Основные определения

Определение 6.1.

Функция f(x) называется непрерывной в точке x0, если она определена в некоторой окрестности этой точки, существует предел limx→x0f(x) и

limx→x0f(x)=f(x0).(6.1)

Подчеркнем, что в определении непрерывности функции в точке x0, в отличие от определения предела функции в этой точке, рассматривается полная, а не проколотая окрестность точки x0 (см. определение 1.13), и пределом функции при x→x0 является значение функции в точке x0.

Если функция f(x) непрерывна в точке x0, то пишут f(x)∈C(x0).

Определение 6.1 непрерывности функции f(x) в точке x0, выраженное  равенством (6.1), сформулируем на "языке ε−δ" в следующем виде:

f(x)∈C(x0)⇔∀ε>0  ∃δ>0:∀x, |x−x0|<δ⇒|f(x)−f(x0)|<ε,

или

∀x, x0−δ<x<x0+δ⇒f(x0)−ε<f(x)<f(x0)+ε.

То же определение запишем на "языке окрестностей":

f(x)∈C(x0)⇔∀Oε(f(x0))  ∃Oδ(x0):∀x∈Oδ(x0)⇒f(x)∈Oε(f(x0)).

Приведем геометрическую интерпретацию определения непрерывности функции f(x) в точке x0 (рис. 6.1).

Рассмотрим кривую y=f(x) и точку M(x0,f(x0)) на ней. Зададим произвольное ε>0 и отметим точки f(x)−ε и f(x)+ε на оси Oy. Найдем на оси Ox две точки A1 и A2, соответствующие точкам f(x)−ε иf(x)+ε на оси Oy. Примем за δ расстояние от точки x0 до ближайшей из точек A1 и A2, и отметим точкиx0−δ и x0+δ на оси Ox. Очевидно, что для любого x∈(x0−δ,x0+δ) Соответствующие значения функции удовлетворяют неравенству f(x0)−ε<f(x)<f(x0)+ε, что и означает непрерывность функции f(x) в точке x0.

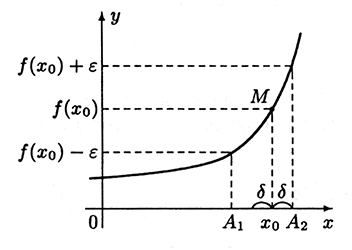
Рис. 6.1

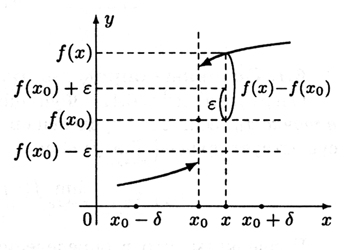
Рис. 6.2

Рассмотрим функцию, график которой приведен на рис. 6.2. В точке x0 значение этой функции равно f(x0).Выберем ε>0 так, как показано на рисунке. Как бы мало ни было δ>0, среди значений x,удовлетворяющих неравенству |x−x0|<δ, есть такие, а именно большие x0, что для них разность f(x)−f(x0)>ε. Следовательно, функци не будет непрерывной в точке x0.

Отметим, что  определение 6.1 непрерывности функции f(x) в точке x0 можно сформулировать и в таком виде: функция y=f(x) называется непрерывной в точке x0, если limx→x0(f(x)−f(x0))=0, илиlimΔx→0Δy=0, где Δy=f(x)−f(x0)− приращение функции, Δx=x−x0− приращение аргумента в точке x0. Другими словами, функция f(x) называется непрерывной в точке x0, если бесконечно малому приращению аргумента в точке x0 соответствует бесконечно малое приращение функции в этой точке.

Определение 6.2.

Функция f(x) называется непрерывной справа в точке x0 (обозначают f(x)∈C+(x0)), если f(x)определена в точке x0 и некоторой ее правой полуокрестности и правый предел функции в точке x0равен значению функции в этой точке, т.е. f(x+0)=f(x0). Иначе это определение можно записать в виде

f(x)∈C+(x0)⇔∀ε>0 ∃δ>0:∀x, x0<x<x0+δ⇒f(x0)−ε<f(x)<f(x0)+ε.

Определение 6.3.

Функция f(x) называется непрерывной слева в точке x0 (обозначают f(x)∈C−(x0)), если f(x)определена в точке x0 и некоторой ее левой полуокрестности и левый предел функции в точке x0равен значению функции в этой точке, т.е. f(x−0)=f(x0). В символической форме это определение имеет вид

f(x)∈C−(x0)⇔∀ε>0 ∃δ>0:∀x, x0−δ<x<x0⇒f(x0)−ε<f(x)<f(x0)+ε.

На рис. 6.3 приведен пример функции, непрерывной справа в точке x0, на рис. 6.4 — непрерывной слева в точке x0. Непрерывность функции слева или справа в некоторой точке называется односторонней непрерывностью.

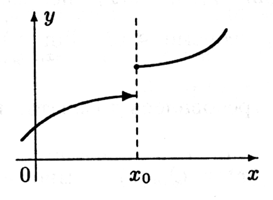
Рис. 6.3

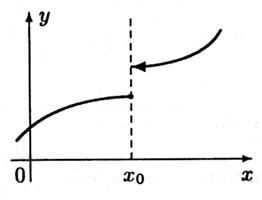
Рис. 6.4

Замечание 6.1.

Из определений  6.1,  6.2 и 6.3 следует, что для непрерывности функции f(x) в точке x0необходимо и достаточно, чтобы f(x) была непрерывна и справа, и слева в точке x0, т.е. чтобы выполнялись следующие равенства:

f(x+0)=f(x−0)=f(x0).