
- •4,Ошибка воспроизведения.
- •5. Основные принципы управления. Разомкнутые системы. Управление с внутренней моделью.
- •6. Селективная инвариантность до при гармоническом задающем воздействии.
- •Вопрос 7. Описание звеньев сау. Уравнение звена в изображениях и передаточная функция.
- •Операторная (символическая) форма записи уравнения элемента
- •8 Чувствительность систем управления к изменению параметров
- •10. Понятие об инвариантных системах
- •12.Понятие о качестве сау. Точность работы сау в установившемся режиме.
- •1. Понятие о качестве системы
- •2. Точность работы сау в установившемся режиме.
- •13 Передаточные функции сау с прямой и обратой связью
- •14. Логарифмические частотные характеристики основных сомножителей передаточной функции
- •15. Реакция линейной замкнутой системы на внешние воздействия. Ду замкнутой системы. Пример
- •16. Вычисление коэффициентов ошибок с помощью передаточной функции по ошибке. Пример.
- •Вопрос17. Стандартная форма представления передаточной функции разомкнутой системы.
- •20. Функция чувствительности и дополнительная функция чувствительности. Интуитивные требования к выбору управляющего устройства.
- •21. Корневые методы оценки качества переходного процесса. Оценка быстродействия.
- •22. Математическая модель двигателя постоянного тока
- •23 Понятие об устойчивости сау
- •24. Селективная абсолютная инвариантность к задающему воздействию в системах с единичной обратной связью. Принцип внутренней модели.
- •25. Алгебраический критерий устойчивости Гурвица.
- •26. Правила преобразования структурных схем.
- •27. Относительная устойчивость.
- •30( Как62). Фомирование частотных характеристик замкнутой системы. Ограничения на дополн. Ф-ю чувств. Смешанн чувствит.
- •32. Коррекция системы с опережением по фазе(реальный пд-регулятор)
- •34. Коррекция с помощью ку с отставанием по фазе
- •35. Уравнение звена в символической форме.
- •36. Понятие о корневом годографе.
- •Вопрос 37. Описание элементов сау. Линеаризация.
- •38 Понятие о коэффициентах ошибок
- •Вычисление коэффициентов ошибок с помощью пф по ошибке
- •39. Передаточные функции системы с единичной обратной связью.
- •40. Критерий Найквиста для случая устойчивой разомкнутой системы. Критический коэффициент усиления.
- •41. Критерий Найквиста для случая неустойчивой разомкнутой системы.
- •42. Линеаризация математической модели бака с жидкостью.
- •43 Понятие о коэффициентах ошибок
- •Коэффициенты ошибок статических и астатических систем.
- •44.(Вкл в себя72) Количественная оценка неопределенностей модели объекта
- •45. Типовые динамические звенья и их характеристики. Интегрирующее звено. Дифференцирующие и форсирующие звенья.
- •46. Критерий Найквиста для случая нейтрально-устойчивой разомкнутой системы.
- •Вопрос 47. Афх разомкнутой системы и ее предельные значения.
- •1) Замкнутая система неустойчива
- •50. Обеспечение астатизма по возмущающему воздействию.
- •2) Уравнение звена в изображениях. Передаточная функция звена (пф)
- •53 Минимально-фазовые звенья
- •54. Введение связей по возмущению
- •55. Построение лчх разомкнутой системы. Правила построения лачх. Пример.
- •56. Частотные методы оценки качества переходного процесса.
- •Вопрос 57. Ошибка по возмущению.
- •58 Робастное качество.
- •59.Задача слежения и регулирования. Возмущения и ограничения.
- •60. Критерий Михайлова.
- •61. Показатели качества работы сау в переходном процессе при ступенчатом воздействии
- •62. Формирование частотных характеристик замкнутой системы
- •64, Параметрический синтез сау по методу лчх
- •65. Понятие о синтезе системы. Требования к проектируемой системе.
- •66. Методы робастного управления
- •67. Устойчивость по входу.
- •71.Внутренняя устойчивость замкнутой системы.
- •72. (Из44) Аддитивная и мультикативная неопределенности.Представление неопределенности в частотной (комплексной) области.
Вопрос 37. Описание элементов сау. Линеаризация.
Элементом САУ называется устройство, преобразующее один процесс (входное воздействие) в другой процесс (выходную реакцию), другими словами, устройство, которое осуществляет преобразование «вход-выход». Необходимо получить математическую модель элемента, т.е. его описание на каком-либо формальном языке.
Универсальным языком теоретического естествознания, служащим для математического моделирования взаимосвязей процессов в природе и технике, является язык уравнений – алгебраических и, в особенности, дифференциальных.
Под математической моделью элемента мы понимаем ДУ элемента, связывающее выходные и входные величины элемента. Это есть описание преобразования «вход-выход» в неявной форме.
Схематическое представление элемента
Э лемент,
представленный своим уравнением
(математической моделью), называется
звеном.
лемент,
представленный своим уравнением
(математической моделью), называется
звеном.
Обычно уравнение элемента получают аналитическим путем, используя законы природы, которые положены в основу принципа действия элемента (модели типа «белый ящик»). Другой путь - идентификация: определение математической модели сложных элементов, обычно объектов управления, экспериментальным путем (модели типа «черный ящик»).
Наиболее общей
математической моделью динамического
элемента является нелинейное ДУ (НЛДУ)
следующего вида
![]() ,(1)
где F
– нелинейная функция;
,(1)
где F
– нелинейная функция;
![]() ;
;
![]() .
Здесь n
– порядок уравнения, определяющий и
порядок элемента. Уравнение (1) называют
уравнением
динамики
элемента.
.
Здесь n
– порядок уравнения, определяющий и
порядок элемента. Уравнение (1) называют
уравнением
динамики
элемента.
Заметим, что выход динамического (инерционного) элемента зависит от настоящего значения входа и прошлых значений входа и выхода в отличие от статического (безинерционного) элемента, выход которого зависит лишь от настоящего значения входа.
Уравнение статики
элемента.
Пусть входное воздействие – постоянная
величина,
![]() ,
так что
,
так что
![]() .
.
Пусть существует
такое
![]() ,
которое обращает уравнение (1) в тождество.
При этом
,
которое обращает уравнение (1) в тождество.
При этом
![]() .
Такой режим, с постоянными значениями
на входе и выходе, носит название
состояние
равновесия
(покоя, номинальный режим работы, рабочая
точка).
.
Такой режим, с постоянными значениями
на входе и выходе, носит название
состояние
равновесия
(покоя, номинальный режим работы, рабочая
точка).
Подставляя в
уравнение динамики (1) вместо y
и v
соответственно
![]() и
и
![]() ,
получаем уравнение статики элемента:
,
получаем уравнение статики элемента:
![]() .
(2)
.
(2)
Разрешая (1)
относительно выходного сигнала, находим
уравнение статики
![]() ,
записанное в другом виде. Уравнение
статики является нелинейным алгебраическим
уравнением. График зависимости
называется статической
характеристикой
элемента. Как пример, на рисунке ниже
показана статическая характеристика
электронного прибора.
,
записанное в другом виде. Уравнение
статики является нелинейным алгебраическим
уравнением. График зависимости
называется статической
характеристикой
элемента. Как пример, на рисунке ниже
показана статическая характеристика
электронного прибора.
З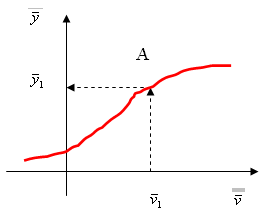 ная
график, легко определить выход
ная
график, легко определить выход
![]() по известному входу
по известному входу
![]() ,
не решая уравнения статики. При этом
точка А с координатами (
,
)
называется рабочей
точкой.
Элементы, описываемые нелинейными
алгебраическими (НАУ) или дифференциальными
уравнениями (НЛДУ), называются нелинейными.
Уравнение элемента описывает свойства
элемента в неявном виде. Для анализа
свойств элемента в явном виде надо
решить следующую задачу.
,
не решая уравнения статики. При этом
точка А с координатами (
,
)
называется рабочей
точкой.
Элементы, описываемые нелинейными
алгебраическими (НАУ) или дифференциальными
уравнениями (НЛДУ), называются нелинейными.
Уравнение элемента описывает свойства
элемента в неявном виде. Для анализа
свойств элемента в явном виде надо
решить следующую задачу.
Известно уравнение (1) и v(t), и необходимо определить y(t). Если элемент нелинейный, то трудно решить НЛДУ. Но существуют приемы, позволяющие упростить математическую модель. К таким приемам относится в первую очередь линеаризация.
Линеаризация – процесс преобразования нелинейной математической модели элемента (1) в эквивалентное, при определенных условиях, линейное ДУ.
Пусть нелинейный
элемент находится в состоянии равновесия,
при этом выход и вход характеризуется
![]() и
и
![]() .
Предположим, что входное воздействие
отклонилось от
,
а значит (по 1) отклонится и выход от
,
так что
.
Предположим, что входное воздействие
отклонилось от
,
а значит (по 1) отклонится и выход от
,
так что
![]() ,
,
![]() .
.
Здесь
![]() - отклонение выхода,
- отклонение выхода,
![]() - отклонение входа.
- отклонение входа.
Отсюда отклонения от нуля i - ых производных выхода и входа:
![]()
при
=const,
![]() при
=const.
при
=const.
Подставляя в (1)
![]() ,
,![]() ,получаем уравнение нелинейного элемента
в отклонениях (приращениях)
,получаем уравнение нелинейного элемента
в отклонениях (приращениях)
![]() .
(3)
.
(3)
Предположим, что нелинейная функция однозначна и дифференцируема по всем своим аргументам, по крайней мере, в окрестности точки А, соответствующей положению равновесия, т.е. существуют частные производные функции F в окрестности точки А, разложение в окрестности точки ( , ). При этом можно разложить F в ряд Тейлора в окрестности точки А:
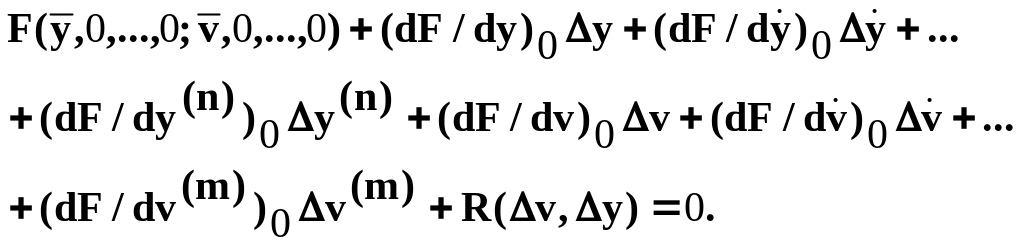 (4)
(4)
Здесь R – остаточный член разложения в ряд.
Предположим, что
отклонения выхода и входа
и
,
и их производных являются малыми, при
этом можем пренебречь R,
т.е. считать, что
![]() в
виду малости по сравнению с другими
членами разложения, т.к. он включает
слагаемые, содержащие отклонения
и
в степени выше первой. Принимая во
внимание уравнение (2) и вышесказанное
относительно R,
можно записать уравнение (4) в виде
в
виду малости по сравнению с другими
членами разложения, т.к. он включает
слагаемые, содержащие отклонения
и
в степени выше первой. Принимая во
внимание уравнение (2) и вышесказанное
относительно R,
можно записать уравнение (4) в виде
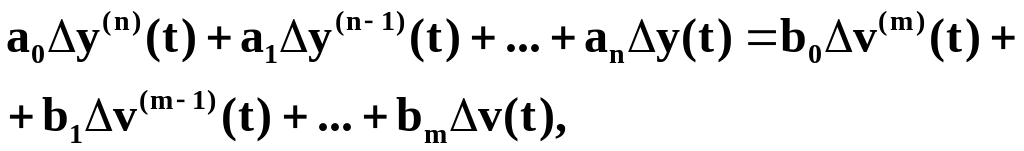 (5)
(5)
Где
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
(6)
.
(6)
Индекс «0»
в уравнениях (4) и (6) означает, что после
определения частных производных заменяем
y
на
![]() ,
v
на
,
v
на
![]() .
Следовательно,
.
Следовательно,
![]() и
и
![]() - постоянные коэффициенты, а уравнение
(5) является линейной
математической моделью элемента (ЛДУ
с постоянными коэффициентами).
- постоянные коэффициенты, а уравнение
(5) является линейной
математической моделью элемента (ЛДУ
с постоянными коэффициентами).
Как видим, сущность линеаризации заключается в замене нелинейного ДУ (3) линейным ДУ (5). Такая замена справедлива при малых отклонениях входа и выхода элемента, т.е. уравнения (3) и (5) эквивалентны только при выполнении данного условия.
Заметим, что уравнение (5) , называемое линеаризованным уравнением элемента, отражает его нелинейные свойства. Действительно, при изменении рабочей точки, т.е. при другом постоянном входе, изменяются в соответствии с выражением (6) коэффициенты уравнения (5).
