53. Неопределенность вида ноль на ноль, бесконечность на бесконечность и др. Примеры раскрывания неопределенностей.

Правило Бернулли^[1]-Лопита́ля — метод нахождения пределов функций раскрывающий неопределённости вида 0 / 0 и  . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения ихпроизводных.

Условия:

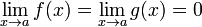1.  или  ;

2.  и   дифференцируемы в проколотой окрестности  ;

3.  в проколотой окрестности  ;

4. существует  ,

тогда существует  .

Пределы также могут быть односторонними.

Докажем теорему для случая, когда пределы функций равны нулю (то есть неопределённость вида  ).

Поскольку мы рассматриваем функции f и g только в правой проколотой полуокрестности точки a, мы можем непрерывным образомих доопределить в этой точке: пусть f(a) = g(a) = 0. Возьмём некоторый x из рассматриваемой полуокрестности и применим к отрезку   теорему Коши. По этой теореме получим:

,

но f(a) = g(a) = 0, поэтому  .

Дальше, записав определение предела отношения производных и обозначив последний

через A, из полученного равенства выводим:

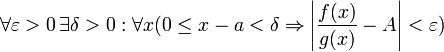 для конечного предела и

 для бесконечного,

что является определением предела отношения функций.