35.  Производные элементарных функций.

Функция	Производная
y= xn	y =n xn−1
y = x	y =1
Y=корень из х	y =1/2 x
y=x/1	y =−1/x2
y = cos x	y =−sinx
y = sin x	y =cosx
y = tg x	y =1/cos2x
y = ctg x	y =−1/sin2x
y = arcsin x	y =1/ 1−x2
y = arccos x	y =−1/ 1−x2
y = arctg x	y =1/1+x2
y = arcctg x	y =−1/1+x2
y=ax a 0 a =1	y =ax lna a 0 a =1
y=ex	y =ex
y=logax a 0 a =1	y =1/x lna
y = lnx	y =1/х x 0

36. Производные суммы, разности, произведения и частного функции.

 Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

(f + g)’ = f ’ + g ’

(f − g)’ = f ’ − g ’

Производная произведения

(f · g) ’ = f ’ · g + f · g ’

Производная деления

37. Дифференцирование сложной функции. Пример. 

Позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке x₀, а функция g имеет производную в точке y₀ = f(x₀), то сложная функция h(x) = g(f(x)) также имеет производную в точке x₀.

38. Уравнение касательной к графику функции в точке. Уравнение нормали к касательной.

Уравнение касательной

Пусть функция y=f(x) дифференцируема в точке х нулевое.Прямая, определяемая уравнение называется уравнением касательной

y = f(а) + f '(a)(x – a)

в точке M(3; – 2).

y = 5x – 17 – уравнение касательной.

Уравнение нормали

Прямая, перпендикулярная касательной в точке касания М(х0:y0), называется нормалью к графику функции y=f(x)

Y=f(x0)-1/f’(x0)*(x-x0)

39. Локальный экстремум функции в точке. Необходимое условие локального экстремума. 

Пусть функция   определена в некоторой окрестности  ,  , некоторой точки   своей области определения. Точка   называется точкой локального максимума, если в некоторой такой окрестности   выполняется неравенство   (  ), и точкой локального минимума, если    .

Необходимое условие

• Лемма Фарма. Пусть функция 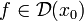  дифференцируема в точке локального экстремума x₀. Тогда:

.

• Если в точке экстремума существует первая частная производная (по какому-либо аргументу), то она равна нулю.

40. Теорема т.Роля о нуле производной. Геометрический смысл теоремы.

Теорема Ро́лля (теорема о нуле производной) утверждает, что Если вещественная функция непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производной функции равна нулю.

Геометрический смысл теоремы.

Теорема утверждает, что если ординаты обоих концов гладкой кривой равны, то на кривой найдется точка, в которой касательная к кривой параллельна оси абсцисс.

41. Формула Ла Гранжа. Геометрический смысл. 

Формула конечных приращений или теорема Лагра́нжа о среднем значенииутверждает, что если функция f непрерывна на отрезке [a;b] и дифференцируема в интервале (a;b), то найдётся такая точка  , что

.

Геометрический смысл.

Геометрически это можно переформулировать так: на отрезке [a;b] найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.

42. Теорема о постоянстве функции, имеющем на интервале равную нулю производную. Теорема с доказательством.

Если функция   дифференцируема на интервале (a;b), и если всюду

на этом интервале  , то функция   является постоянной на этом интервале.Доказательство. Зафиксируем некоторую точку x0 из интервала (a;b) и возьмём любую другую точку  x из этого интервала. Отрезок [x0, x] целиком принадлежитинтервалу (a;b),  поэтому функция   дифференцируема, а, следовательно, и непрерывна всюду на отрезке [x0, x]. Это значит, что для функции   на отрезке [x0, x] выполнены условия теоремы Лагранжа. Следовательно, внутри отрезка [x0, x] найдётся такая точка c, что  .  Но так как по условию всюду на интервале (a;b)  , то и  , а, следовательно,  . Это равенство означает, что значение функции   в произвольной точке интервала (a;b) равно её значению в фиксированной точке x0, то есть функция    постоянна всюду на интервале (a;b).

Теорема доказана.