15. Точки разрыва функции

Точка называется точкой разрыва функции , если в ней нарушается хотя бы одно из трёх условий непрерывности функции в точке, указанных в параграфе 14.

В качестве примера возьмём функцию, определённую формулой

. (21)

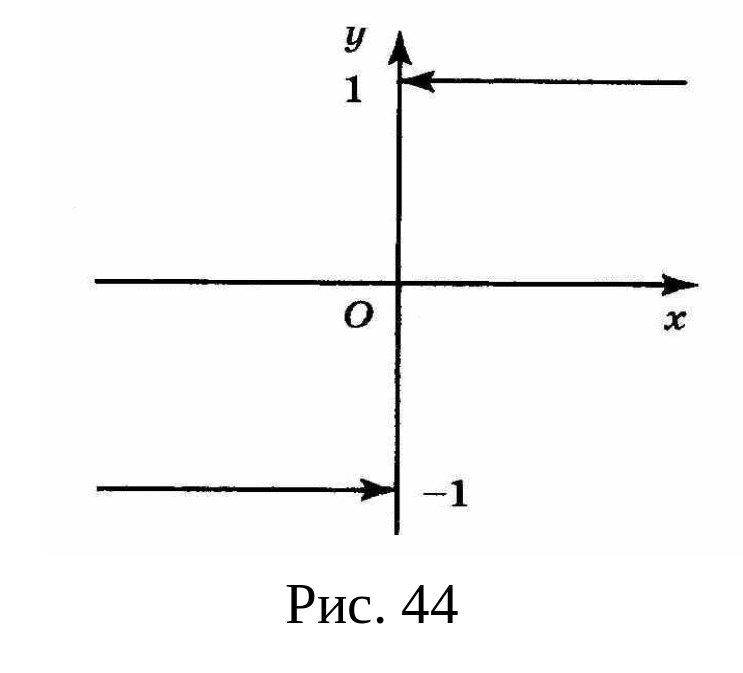
Ясно, что эта функция определена везде, кроме точки . Для любого положи-тельного имеем и согласно формуле (21) . Если же , то и . График этой функции изображен на рис. 44.

Так как функция в точке не определена, то на её графике нет точки с абсциссой , т. е. нет точки, лежащей на оси , поэтому график как бы не доходит до оси , что отмечено стрелками. Для любой точки имеем . Кроме того, для любого имеем , поэтому . Это означает, что функция в точке непрерывна в силу (16). Аналогично установим, что для любого функция также непрерывна. Но точка есть точка разрыва функции (21) по двум причинам:

• не существует 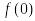, т. к. в точке функция (21) не определена;

• для функции (21) не существует предел .

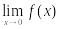В самом деле, предел справа этой функции , а предел слева . Таким образом, односторонние пределы хотя и существуют, но не равны друг другу, значит, не существует обычный (двусторонний) предел .

Т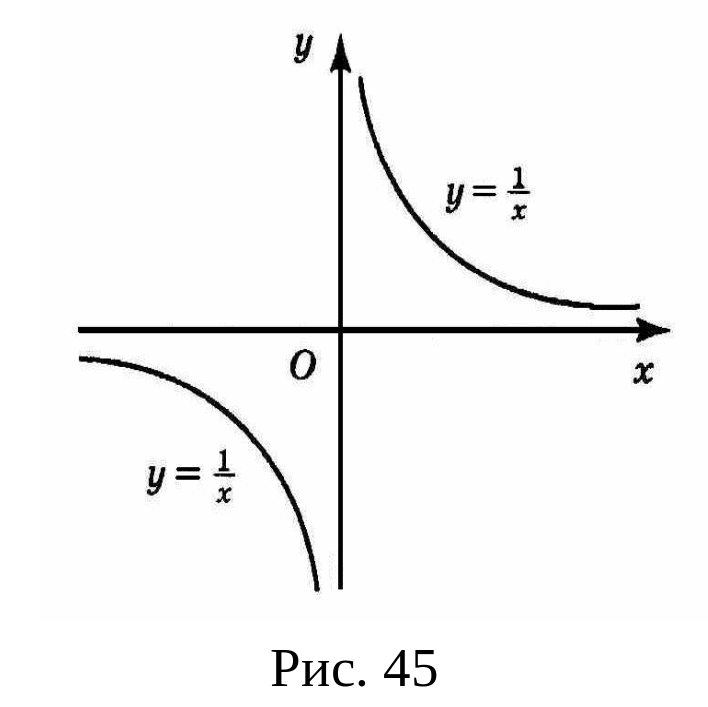 очка называется точкой разрыва первого рода функции , если существуют конечные односторонние пределы и . Например, для функции (21) точка – точка разрыва первого рода. Все остальные точки разрыва называются точками разрыва второго рода. Для функции (рис. 45) точкой разрыва второго рода будет , так как в этой точке функция не определена и односторонние пределы бесконечны: и

16. Задача об определении скорости

П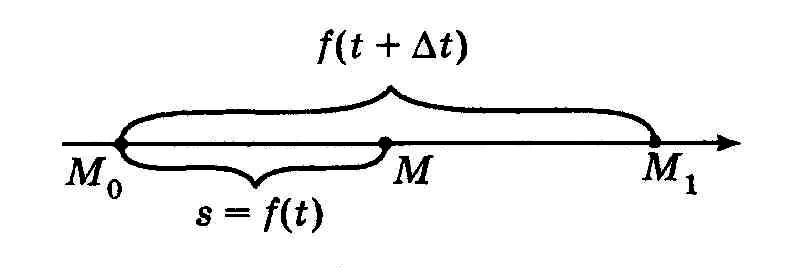 усть точка движется по прямой неравномерно и проходит путь от точки до точки длиной за время (рис. 46). С изменением длина пути изменяется по заданному закону (т. е. функцию считаем заданной). Итак, . В следующий момент времени , , точка окажется в положении . Таким образом, за время точка пройдёт путь, равный (получаемый из формулы заменой на ). Это означает, что за время точ-

Рис. 46 ка проходит путь

(1)

Путь равен приращению функции , соответствующему приращению и вычисляемому для точки . Ясно, что отношение характеризует быстроту передвижения точки на участке за время . Чем быстрее точка движется, тем больший путь она пройдёт за время , тем больше будет значение этого отношения. Нас интересует быстрота движения точки не на всём участке (не за весь промежуток времени ), а быстрота движения точки в положении (в момент ).

Очевидно, что чем меньше , тем лучше отношение характеризует быстроту движения точки в момент . Эту последнюю быстроту наиболее полно характеризует предел , который называется скоростью движения точки в момент и обозначается . Итак, или с учётом (1)

. (2)