9.Понятие об энтропии. Энтропия идеального газа. Статистическое истолкование второго начала термодинамики. Теорема Нернста.

Кроме внутренней энергии U, которая является однозначной функцией параметров состояния системы T и V, в термодинамике широко используются и другие функции состояния (свободная энергия, энтальпия, энтропия и т. д.). Энтропия как функция состояния выделяется среди других термодинамических функций тем, что имеет статистическую, т. е. вероятностную, природу. В термодинамике понятие энтропия вводится с помощью приведенного количества теплоты Q^*. В изотермическом процессе Q^* = Q/T. Если температура не постоянна (Т  const), то произвольный процесс нужно разбить на бесконечно малые участки, где температуру можно считать постоянно, и ввести элементарное приведенное количество теплоты Q^* = Q/Т. Приведенная теплота на конечном участке 1−2 этого процесса будет определяться интегралом: 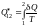. Для любого обратимого цикла: 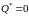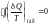 . Отсюда следует, что подынтегральное выражение (Q/T)_o6p является полным дифференциалом некоторой функции S, которую называют энтропией. Таким образом, для обратимого процесса изменение энтропии определяется выражениями dS =  . 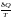Энтропия как функция состояния системы обладает уникальным свойством: энтропия замкнутой системы при любых происходящих в ней процессах не может убывать. Она остается постоянной в обратимых процессах и возрастает в необратимых. Следовательно, имеет место закон возрастания энтропии: S  0. − статистическая формулировка второго начала термодинамики. Больцман показал, что энтропия S пропорциональна логарифму вероятности состояния: S = k lnW, где k – постоянная Больцмана; W – вероятность данного состояния.

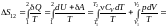
Изменение энтропии идеального газа. Найдем изменение энтропии идеального газа при любом произвольном процессе . (12.10.10)

Третье начало термодинамики (или теорема Нернста) было открыто в 1906 г. В. Нернст в процессе термодинамического исследования изменения энтропии химических реакций. Оно тесно связано с поведением теплоемкости при абсолютном нуле температур. Теорема Нернста утверждает, что при приближении к абсолютному нулю энтропия системы также стремится к нулю независимо от того, какие значения принимают все остальные параметры состояния системы: 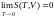. Поскольку энтропия равна 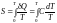, а температура Т стремится к нулю, теплоемкость вещества также должна стремиться к нулю, причем быстрее, чем Т. Отсюда следует недостижимость абсолютного нуля температуры при конечной последовательности термодинамических процессов, т. е. конечного числа операций − циклов работы холодильной машины.

10. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса.

Между ат. и мол-ми вещества на малых расстояниях действуют силы отталкивания F_o , а на больших − силы притяжения F_п. В случае простых неполярных веществ притяжение в основном обусловлено взаимодействием наведенных дипольных моментов молекул. Эти сравнительно слабые ван-дер-ваальсовы силы зависят от расстояния r между молекулами по степенному закону (F  r⁻ⁿ). Область их действия порядка 10⁻⁹ м. Для двух молекул простых веществ явный вид потенциальной энергии Ф(r) взаимодействия, которое описывается потенциалом Леннарда − Джонса, имеет вид 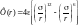. Значения величин  и  - в справочнике. Наличие сил притяжения и отталкивания приводит к тому, что при больших давлениях поведение реального газа будет отличаться от модели идеального газа. Одно из наиболее известных приближенных уравнений описывающих состояние реального газа было предложено голландским физиком Ван-дер-Ваальсом - базируется на законе Менделеева − Клапейрона и содержит два параметра (а и b), с помощью которых учитывается вклад сил притяжения на больших расстояниях и сил отталкивания на малых расстояниях между молекулами реального газа. Силы отталкивания противодействуют проникновению данной частицы в ту область объема сосуда, которая занята другими молекулами. Собственный объем V₀ , занятый частицей, представляется как объем шара с некоторым эффективным диаметром d. Поэтому «свободный объем» V ^*, в котором могут свободно (как в идеальном газе) двигаться молекулы реального газа, будет на некоторую величину меньше, чем объем V, занимаемый газом. «Свободный объем» будет равен V ^* = V − b, где b − поправочный коэффициент для одного моля газа. Приближенные расчеты показывают, что объем, занятый молекулой, равен учетверенному собственному объему этой молекулы V₀ . Тогда поправка b равна b = 4N_a V₀ . Наличие сил притяжения между молекулами приводит к дополнительному «внутреннему» давлению рⁱ, которое оказывается обратно пропорциональным квадрату V 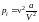, где a − второй поправочный коэффициент. В результате внешнее давление р, которое необходимо приложить к реальному газу для удержания его в заданном объеме V, уменьшается по сравнению с давлением р^* в случае идеального газа. Это значит, что 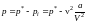. Свободный объем V ^* и давление р^* связаны уравнением Клапейрона – Менделеева р^* V ^* = RT. Приближенное уравнение состояния для реального газа 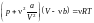. Следует отметить, что уравнение Ван-дер-Ваальса лучше согласуется с опытными данными, чем уравнение Клапейрона −Менделеева, особенно при больших давлениях. Проведем анализ уравнения Ван-дер-Ваальса. С этой целью построим зависимости давления от объема газа при постоянной температуре для нескольких значений температуры (Т₁  Т₂  Т_к  Т₃  Т₄). Полученные кривые − изотермы Ван-дер-Ваальса, оказываются довольно своеобразными: при низких температурах они имеют волнообразные участки (максимумы и минимумы), при некоторой температуре Т_к на изотерме имеется только точка перегиба К, при высоких температурах изотермы Ван-дер-Ваальса похожи на изотермы идеального газа. С математической точки зрения такой характер изотерм объясняется очень просто. Если привести уравнение Ван-дер-Ваальса к нормальному виду, то оно окажется кубическим уравнением относительно объема V. Кубическое уравнение может иметь либо три вещественных корня, либо один вещественный корень и два мнимых. 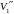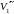Очевидно, что первому случаю соответствуют изотермы при низких температурах (три значения объема газа , , отвечают одному значению давления p₁), а второму случаю − изотермы при высоких температурах (одно значение объема V₄ отвечает одному значению давления р₄) (рис. 13.1.2).