- •1. Теплота и работа. Первое начало термодинамики.
- •2. Первое начало термодинамики при изохорическом, изобарическом и изотермическом процессах.
- •3. Теплоёмкость тела и вещества.
- •4. Адиабатический процесс. Уравнение Пуассона.
- •5. Политропические процессы.
- •6. Второе начало термодинамики. Обратимые и необратимые термодинамические процессы.
- •7. Круговой процесс. Тепловые и холодильные машины.
- •8. Идеальная тепловая машина Карно и её кпд.
- •9.Понятие об энтропии. Энтропия идеального газа. Статистическое истолкование второго начала термодинамики. Теорема Нернста.
- •10. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса.
- •11. Экспериментальные изотермы реального газа. Опыт Эндрюса.
- •1 2. Понятие фазовых переходов. Критические параметры и их связь с поправками Ван-дер-Ваальса.
- •13. Внутренняя энергия реального газа.
- •14. Эффект Джоуля-Томпсона.
- •15. Электрический заряд. Свойства электрического заряда. Закон сохранения электрического заряда. Закон Кулона.
- •16. Электростатическое поле. Напряженность электростатического поля. Силовые линии. Принцип суперпозиции электростатических полей.
- •17. Поток вектора напряженности электростатического поля. Теорема Гаусса для электростатического поля в вакууме в интегральной и дифференциальной формах.
- •18. Работа по перемещению электрического заряда в электростатическом поле.
- •19. Теорема о циркуляции вектора напряженности электростатического поля в интегральной и дифференциальной формах.
- •20. Потенциал. Разность потенциалов. Принцип суперпозиции для электростатических потенциалов.
- •22. Электрический диполь. Электрический момент диполя. Напряженность и потенциал поля диполя.
- •23. Диполь во внешних однородном и неоднородном электростатических полях. Энергия диполя во внешнем электростатическом поле.
- •26. Вектор поляризации. Диэлектрическая восприимчивость полярных и неполярных диэлектриков.
- •27. Теорема Гаусса для электростатического поля в диэлектрике. Вектор электрического смещения.
- •28. Диэлектрическая проницаемость среды. Условия на границе раздела двух диэлектрических сред.
- •29. Сегнетоэлектрики. Диэлектрический гистерезис. Температура Кюри.
- •30. Электрическое поле внутри проводника и вблизи его поверхности. Электростатическая защита.
- •31. Электроемкость уединенного проводника и конденсатора. Электроемкость уединенного проводящего шара.
- •32. Конденсаторы (плоский, сферический, цилиндрический) и их соединения.
- •33. Энергия системы зарядов, проводника и конденсатора. Объемная плотность энергии электрического поля.
- •34. Условия существования и характеристики постоянного электрического тока.
- •35. Законы Ома в интегральной и дифференциальной формах.
- •36. Работа и мощность тока. Закон Джоуля-Ленца в интегральной и дифференциальной формах.
- •37. Магнитное поле. Вектор магнитной индукции. Линии магнитной индукции.
- •38. Принцип суперпозиции магнитных полей. Закон Био-Савара-Лапласа.
- •39. Расчет магнитных полей прямого проводника с током бесконечной и конечной длины.
- •40. Магнитное поле движущегося электрического заряда.
- •41. Циркуляция вектора магнитной индукции. Теорема и циркуляции вектора магнитной индукции в вакууме в интегральной и дифференциальной форме.
- •42. Магнитное поле тороида и соленоида.
- •43. Магнитный поток. Теорема Гаусса для магнитного поля в интегральной и дифференциальной формах.
- •44. Сила Ампера. Взаимодействие параллельных проводников с током.
- •45. Магнитный момент контура с током. Механический момент, действующий на контур с током в однородном магнитном поле.
- •46. Работа перемещения проводника и контура с током в магнитном поле.
- •47. Сила Лоренца. Масс-спектрометрия.
- •48. Эффект Холла.
- •49. Опыты Фарадея. Закон электромагнитной индукции. Вихревое электрическое поле. Токи Фуко.
- •50. Явление самоиндукции. Индуктивность.
- •51. Энергия контура с током. Энергия и объёмная плотность энергии магнитного поля.
- •52. Атом в магнитном поле. Магнитные моменты электронов и атомов. Орбитальный и спиновой магнитные моменты.
- •53. Намагниченность. Микротоки и макротоки. Магнитная восприимчивость и магнитная проницаемость среды.
- •54. Типы магнетиков. Магнитная восприимчивость диамагнетиков и парамагнетиков.
- •55. Элементарная теория диа- и парамагнетизма.
- •56. Ферромагнетики. Магнитный гистерезис. Точка Кюри.
- •57. Вихревое электрическое поле. Ток смещения. Первое и второе уравнения Максвелла в интегральной форме.
- •58. Полная система уравнений Максвелла для электромагнитного поля в интегральной и дифференциальной формах. Материальные уравнения. Граничные условия.
- •59. Электромагнитные волны. Волновое уравнение. Основные свойства электромагнитной волны.
- •60. Энергия электромагнитной волны. Вектор Умова — Пойнтинга.
- •61. Интенсивность света при суперпозиции двух монохроматических волн. Интерференция света.
- •62. Время и длина когерентности. Способы получения когерентных волн.
- •6 3. Интерференция света на тонких пленках. Интерференционные приборы.
- •64. Явление дифракции света и условия её наблюдения. Принцип Гюйгенса-Френеля.
- •65. Метод зон Френеля.
- •66. Дифракция Френеля на круглом отверстии и диске.
- •67. Дифракция Фраунгофера на одной щели и на дифракционной решетке.
- •68. Дифракция рентгеновских лучей на кристаллической решетке.
- •69. Спектральные приборы. Разрешающая способность оптических приборов.
- •70. Естественный и поляризованный свет. Поляризация света при отражении и преломлении. Закон Брюстера.
- •71. Двойное лучепреломление. Поляризаторы. Закон Малюса.
43. Магнитный поток. Теорема Гаусса для магнитного поля в интегральной и дифференциальной формах.
Магни́тный
пото́к — поток Фв
как интеграл вектора магнитной индукции
В через конечную поверхность S.
Определяется через интеграл по поверхности
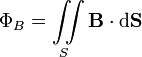 при
этом векторный элемент площади поверхности
определяется как
при
этом векторный элемент площади поверхности
определяется как![]() где n
— единичный вектор, нормальный к
поверхности. Также
магнитный поток можно рассчитать как
скалярное произведение вектора магнитной
индукции на вектор площади:
где n
— единичный вектор, нормальный к
поверхности. Также
магнитный поток можно рассчитать как
скалярное произведение вектора магнитной
индукции на вектор площади:![]() где
α — угол между вектором магнитной
индукции и нормалью к плоскости площади.
Магнитный поток через контур также
можно выразить через циркуляцию
векторного потенциала магнитного поля
по этому контуру:
где
α — угол между вектором магнитной
индукции и нормалью к плоскости площади.
Магнитный поток через контур также
можно выразить через циркуляцию
векторного потенциала магнитного поля
по этому контуру:
Теорема
Гаусса: Поток
вектора магнитной индукции через любую
замкнутую поверхность равен нулю: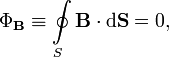 или
в дифференциальной форме
или
в дифференциальной форме
![]() Это
эквивалентно тому, что в природе не
существует «магнитных зарядов»
(монополей), которые создавали бы
магнитное поле, как электрические заряды
создают электрическое поле. Иными
словами, теорема Гаусса для магнитной
индукции показывает, что магнитное поле
является (полностью) вихревым.
Это
эквивалентно тому, что в природе не
существует «магнитных зарядов»
(монополей), которые создавали бы
магнитное поле, как электрические заряды
создают электрическое поле. Иными
словами, теорема Гаусса для магнитной
индукции показывает, что магнитное поле
является (полностью) вихревым.
44. Сила Ампера. Взаимодействие параллельных проводников с током.
Зако́н
Ампе́ра — закон взаимодействия
постоянных токов. Установлен Андре Мари
Ампером в 1820. Из закона Ампера следует,
что параллельные проводники с постоянными
токами, текущими в одном направлении,
притягиваются, а в противоположных —
отталкиваются. Законом Ампера называется
также закон, определяющий силу, с которой
магнитное поле действует на малый
отрезок проводника с током. Сила dF
, с которой магнитное поле действует на
элемент объёма dV проводника с током
плотности j
, находящегося в магнитном поле с
индукцией B:![]() .
Если ток течёт по тонкому проводнику,
то
.
Если ток течёт по тонкому проводнику,
то![]() где
dl
- «элемент длины» проводника — вектор,
по модулю равный dl
и совпадающий по направлению с током.
Тогда предыдущее равенство можно
переписать следующим образом:
где
dl
- «элемент длины» проводника — вектор,
по модулю равный dl
и совпадающий по направлению с током.
Тогда предыдущее равенство можно
переписать следующим образом:
Сила
dF,
с которой магнитное поле действует на
элемент dl
проводника с током, находящегося в
магнитном поле, прямо пропорциональна
силе тока I в проводнике и векторному
произведению элемента длины dl
проводника на магнитную индукцию B
:![]() Направление
силы dF
определяется по правилу вычисления
векторного произведения, которое удобно
запомнить при помощи правила правой
руки. Модуль силы Ампера можно найти по
формуле:
Направление
силы dF
определяется по правилу вычисления
векторного произведения, которое удобно
запомнить при помощи правила правой
руки. Модуль силы Ампера можно найти по
формуле:![]() где
α — угол между векторами магнитной
индукции и тока. Сила dF максимальна
когда элемент проводника с током
расположен перпендикулярно линиям
магнитной индукции
где
α — угол между векторами магнитной
индукции и тока. Сила dF максимальна
когда элемент проводника с током
расположен перпендикулярно линиям
магнитной индукции![]() =>
=>![]() .
.
Наиболее
известным примером, иллюстрирующим
силу Ампера, является следующая задача.
В вакууме на расстоянии r
друг от друга расположены два бесконечных
параллельных проводника, в которых в
одном направлении текут токи I1
и I2.
Требуется найти силу, действующую на
единицу длины проводника. Бесконечный
проводник с током I1
в точке на расстоянии r
создаёт магнитное поле с индукцией:![]() (по закону Био — Савара — Лапласа).
Теперь
по закону Ампера найдём силу, с которой
первый проводник действует на второй:
(по закону Био — Савара — Лапласа).
Теперь
по закону Ампера найдём силу, с которой
первый проводник действует на второй:![]() .
По правилу буравчика,
.
По правилу буравчика,![]() направлена
в сторону первого проводника (аналогично
и для
направлена
в сторону первого проводника (аналогично
и для![]() ,
а значит, проводники притягиваются).
Модуль данной силы (r — расстояние между
проводниками):
,
а значит, проводники притягиваются).
Модуль данной силы (r — расстояние между
проводниками):![]() Интегрируем,
учитывая только проводник единичной
длины (пределы l от 0 до 1):
Интегрируем,
учитывая только проводник единичной
длины (пределы l от 0 до 1):![]()