
- •1. Теплота и работа. Первое начало термодинамики.
- •2. Первое начало термодинамики при изохорическом, изобарическом и изотермическом процессах.
- •3. Теплоёмкость тела и вещества.
- •4. Адиабатический процесс. Уравнение Пуассона.
- •5. Политропические процессы.
- •6. Второе начало термодинамики. Обратимые и необратимые термодинамические процессы.
- •7. Круговой процесс. Тепловые и холодильные машины.
- •8. Идеальная тепловая машина Карно и её кпд.
- •9.Понятие об энтропии. Энтропия идеального газа. Статистическое истолкование второго начала термодинамики. Теорема Нернста.
- •10. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса.
- •11. Экспериментальные изотермы реального газа. Опыт Эндрюса.
- •1 2. Понятие фазовых переходов. Критические параметры и их связь с поправками Ван-дер-Ваальса.
- •13. Внутренняя энергия реального газа.
- •14. Эффект Джоуля-Томпсона.
- •15. Электрический заряд. Свойства электрического заряда. Закон сохранения электрического заряда. Закон Кулона.
- •16. Электростатическое поле. Напряженность электростатического поля. Силовые линии. Принцип суперпозиции электростатических полей.
- •17. Поток вектора напряженности электростатического поля. Теорема Гаусса для электростатического поля в вакууме в интегральной и дифференциальной формах.
- •18. Работа по перемещению электрического заряда в электростатическом поле.
- •19. Теорема о циркуляции вектора напряженности электростатического поля в интегральной и дифференциальной формах.
- •20. Потенциал. Разность потенциалов. Принцип суперпозиции для электростатических потенциалов.
- •22. Электрический диполь. Электрический момент диполя. Напряженность и потенциал поля диполя.
- •23. Диполь во внешних однородном и неоднородном электростатических полях. Энергия диполя во внешнем электростатическом поле.
- •26. Вектор поляризации. Диэлектрическая восприимчивость полярных и неполярных диэлектриков.
- •27. Теорема Гаусса для электростатического поля в диэлектрике. Вектор электрического смещения.
- •28. Диэлектрическая проницаемость среды. Условия на границе раздела двух диэлектрических сред.
- •29. Сегнетоэлектрики. Диэлектрический гистерезис. Температура Кюри.
- •30. Электрическое поле внутри проводника и вблизи его поверхности. Электростатическая защита.
- •31. Электроемкость уединенного проводника и конденсатора. Электроемкость уединенного проводящего шара.
- •32. Конденсаторы (плоский, сферический, цилиндрический) и их соединения.
- •33. Энергия системы зарядов, проводника и конденсатора. Объемная плотность энергии электрического поля.
- •34. Условия существования и характеристики постоянного электрического тока.
- •35. Законы Ома в интегральной и дифференциальной формах.
- •36. Работа и мощность тока. Закон Джоуля-Ленца в интегральной и дифференциальной формах.
- •37. Магнитное поле. Вектор магнитной индукции. Линии магнитной индукции.
- •38. Принцип суперпозиции магнитных полей. Закон Био-Савара-Лапласа.
- •39. Расчет магнитных полей прямого проводника с током бесконечной и конечной длины.
- •40. Магнитное поле движущегося электрического заряда.
- •41. Циркуляция вектора магнитной индукции. Теорема и циркуляции вектора магнитной индукции в вакууме в интегральной и дифференциальной форме.
- •42. Магнитное поле тороида и соленоида.
- •43. Магнитный поток. Теорема Гаусса для магнитного поля в интегральной и дифференциальной формах.
- •44. Сила Ампера. Взаимодействие параллельных проводников с током.
- •45. Магнитный момент контура с током. Механический момент, действующий на контур с током в однородном магнитном поле.
- •46. Работа перемещения проводника и контура с током в магнитном поле.
- •47. Сила Лоренца. Масс-спектрометрия.
- •48. Эффект Холла.
- •49. Опыты Фарадея. Закон электромагнитной индукции. Вихревое электрическое поле. Токи Фуко.
- •50. Явление самоиндукции. Индуктивность.
- •51. Энергия контура с током. Энергия и объёмная плотность энергии магнитного поля.
- •52. Атом в магнитном поле. Магнитные моменты электронов и атомов. Орбитальный и спиновой магнитные моменты.
- •53. Намагниченность. Микротоки и макротоки. Магнитная восприимчивость и магнитная проницаемость среды.
- •54. Типы магнетиков. Магнитная восприимчивость диамагнетиков и парамагнетиков.
- •55. Элементарная теория диа- и парамагнетизма.
- •56. Ферромагнетики. Магнитный гистерезис. Точка Кюри.
- •57. Вихревое электрическое поле. Ток смещения. Первое и второе уравнения Максвелла в интегральной форме.
- •58. Полная система уравнений Максвелла для электромагнитного поля в интегральной и дифференциальной формах. Материальные уравнения. Граничные условия.
- •59. Электромагнитные волны. Волновое уравнение. Основные свойства электромагнитной волны.
- •60. Энергия электромагнитной волны. Вектор Умова — Пойнтинга.
- •61. Интенсивность света при суперпозиции двух монохроматических волн. Интерференция света.
- •62. Время и длина когерентности. Способы получения когерентных волн.
- •6 3. Интерференция света на тонких пленках. Интерференционные приборы.
- •64. Явление дифракции света и условия её наблюдения. Принцип Гюйгенса-Френеля.
- •65. Метод зон Френеля.
- •66. Дифракция Френеля на круглом отверстии и диске.
- •67. Дифракция Фраунгофера на одной щели и на дифракционной решетке.
- •68. Дифракция рентгеновских лучей на кристаллической решетке.
- •69. Спектральные приборы. Разрешающая способность оптических приборов.
- •70. Естественный и поляризованный свет. Поляризация света при отражении и преломлении. Закон Брюстера.
- •71. Двойное лучепреломление. Поляризаторы. Закон Малюса.
41. Циркуляция вектора магнитной индукции. Теорема и циркуляции вектора магнитной индукции в вакууме в интегральной и дифференциальной форме.
Теорема
о циркуляции вектора магнитной индукции
в вакууме:
циркуляция вектора магнитной индукции
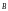 по произвольному замкнутому контуру
равна алгебраической сумме токов,
охватываемых этим контуром, умноженной
на
по произвольному замкнутому контуру
равна алгебраической сумме токов,
охватываемых этим контуром, умноженной
на
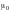 .
Иначе говоря
.
Иначе говоря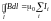 ,г
,г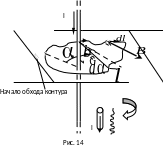 де
де
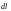 – элементарное перемещение вдоль
замкнутого контура l.
Докажем теорему для случая, когда ток
I
течет по прямому бесконечно длинному
проводнику, а замкнутый контур l
расположен в плоскости, перпендикулярной
току (рис. 14). Циркуляция вектора
магнитной индукции
может быть записана в виде
– элементарное перемещение вдоль
замкнутого контура l.
Докажем теорему для случая, когда ток
I
течет по прямому бесконечно длинному
проводнику, а замкнутый контур l
расположен в плоскости, перпендикулярной
току (рис. 14). Циркуляция вектора
магнитной индукции
может быть записана в виде
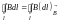 ,
где
– индукция магнитного поля прямого
тока;
,
где
– индукция магнитного поля прямого
тока;
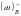 – проекция вектора элементарного
перемещения
на направление вектора
.
– проекция вектора элементарного
перемещения
на направление вектора
.
И
 з
рис. 15 видно, что
з
рис. 15 видно, что
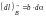 с хорошей степенью точности. Таким
образом,
с хорошей степенью точности. Таким
образом,
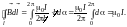 (1.10)
Если изменить направление тока на
рис. 14 на противоположное, то изменится
направление вектора
(1.10)
Если изменить направление тока на
рис. 14 на противоположное, то изменится
направление вектора
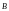 на противоположное в каждой точке
пространства. Противоположной по знаку
станет циркуляция вектора
для выбранного направления обхода
контура. При этом в равенстве (1.10) ток
следует считать отрицательным и
подставлять его значение в формулу
(1.10) со знаком минус. Таким образом, ток
следует считать положительным, если
направление обхода контура связано с
направлением тока правилом правого
винта. В противном случае ток надо
считать отрицательным.Если контур l
не охватывает ток (рис. 16), то
на противоположное в каждой точке
пространства. Противоположной по знаку
станет циркуляция вектора
для выбранного направления обхода
контура. При этом в равенстве (1.10) ток
следует считать отрицательным и
подставлять его значение в формулу
(1.10) со знаком минус. Таким образом, ток
следует считать положительным, если
направление обхода контура связано с
направлением тока правилом правого
винта. В противном случае ток надо
считать отрицательным.Если контур l
не охватывает ток (рис. 16), то
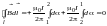 .
.
42. Магнитное поле тороида и соленоида.
Найдем
с помощью теоремы о циркуляции, индукцию
магнитного поля внутри соленоида.
Рассмотрим соленоид длиной l, который
имеет N витков, и по которому течет ток
(рис. 1). Будем считать длину соленоида
во много раз больше, чем диаметр его
витков. Экспериментальное изучение
магнитного поля соленоида показывает,
что внутри соленоида поле однородно,
вне соленоида — неоднородно и практически
отсутствует. На рис. 1 даны линии магнитной
индукции внутри и вне соленоида. Чем
соленоид длиннее, тем магнитная индукция
вне его меньше. Поэтому приближенно
можно полагать, что поле бесконечно
длинного соленоида сосредоточено
целиком внутри него, а поле соленоида
можно не учитывать. Для вычисления
магнитной индукции В выберем замкнутый
прямоугольный контур ABCDA, как показано
на рис. 1. Циркуляция вектора В по
замкнутому контуру ABCDA, который охватывает
все N витков, используя формулу циркуляции
вектора В, будет![]()
Интеграл
по ABCDA можно разложить на четыре интеграла:
по АВ, ВС, CD и DA. На участках АВ и CD контур
и линии магнитной индукции перпендикулярны:
Bl=0. На участке вне соленоида B=0. На участке
DA циркуляция вектора В равна Вl (контур
и линии магнитной индукции совпадают);
значит,![]() (1)
Из
(1) приходим к формуле магнитной индукции
поля внутри соленоида (в вакууме):
(1)
Из
(1) приходим к формуле магнитной индукции
поля внутри соленоида (в вакууме):![]() (2)
Мы
видим, что поле внутри соленоида однородно
(при расчетах пренебрегают краевыми
эффектами в областях, прилегающих к
торцам соленоида). Но отметим, что вывод
этой формулы не совсем корректен
(поскольку линии магнитной индукции
замкнуты, и интеграл по внешнему участку
магнитного поля строго нулю не равен).
Корректно найти поле внутри соленоида
можно, используя закон Био — Савара —
Лапласа; в результате получается такая
же формула (2). Важное практическое
значение имеет также магнитное поле
тороида — кольцевой катушки, у которой
витки намотаны на сердечник, который
имеет форму тора (рис. 2). Магнитное поле,
как известно из опыта, сосредоточено
внутри тороида, а вне его поле равно
нулю. В данном случае линии магнитной
индукции, как следует из соображений
симметрии, есть окружности, у которых
центры расположены по оси тороида. В
качестве контура возьмем одну такую
окружность радиуса r. Тогда, используя
теорему о циркуляции, B•2πr=μ0NI, откуда
следует, что магнитная индукция внутри
тороида (в вакууме)
(2)
Мы
видим, что поле внутри соленоида однородно
(при расчетах пренебрегают краевыми
эффектами в областях, прилегающих к
торцам соленоида). Но отметим, что вывод
этой формулы не совсем корректен
(поскольку линии магнитной индукции
замкнуты, и интеграл по внешнему участку
магнитного поля строго нулю не равен).
Корректно найти поле внутри соленоида
можно, используя закон Био — Савара —
Лапласа; в результате получается такая
же формула (2). Важное практическое
значение имеет также магнитное поле
тороида — кольцевой катушки, у которой
витки намотаны на сердечник, который
имеет форму тора (рис. 2). Магнитное поле,
как известно из опыта, сосредоточено
внутри тороида, а вне его поле равно
нулю. В данном случае линии магнитной
индукции, как следует из соображений
симметрии, есть окружности, у которых
центры расположены по оси тороида. В
качестве контура возьмем одну такую
окружность радиуса r. Тогда, используя
теорему о циркуляции, B•2πr=μ0NI, откуда
следует, что магнитная индукция внутри
тороида (в вакууме)![]() где
N — число витков тороида. Если контур
проходит вне тороида, то токов он не
охватывает и B•2πr = 0. Следовательно, что
поле вне тороида
где
N — число витков тороида. Если контур
проходит вне тороида, то токов он не
охватывает и B•2πr = 0. Следовательно, что
поле вне тороида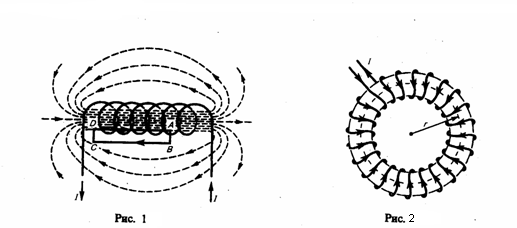 отсутствует (что показывает и опыт).
отсутствует (что показывает и опыт).
