3.2 Параметры распределения

Распределение случайной величины характеризуется параметрами распределения, которые объединены в четыре группы характеристик:

• характеристики положения,

• характеристики рассеивания,

• характеристики асимметрии,

• характеристики эксцесса.

Естественно, что параметры распределения определяются только для данных, представленных либо в интервальной шкале, либо в шкале отношений.

Из характеристик положения рассмотрим моду, медиану и среднее арифметическое значение. По-другому эти параметры называются мерами центральной тенденции.

Мода (М₀) - наиболее часто встречающееся значение; его называют также модальным значением. Кроме модального значения используется также понятие модального интервала - так именуется интервал, куда попадает наибольшее количество значений. Нередко модальное значение оказывается как раз в модальном интервале. Распределение величины может быть унимодальным и полимодальным: если мода в распределении одна - то распределение унимодальное, если более - то полимодальное.

Среднее арифметическое значение М_х рассчитывается по формуле:

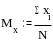
где х_i - это сумма всех значений случайной величины от первого х₁ до последнего x_N, а N - это общее число значений случайной величины.

Медиана (М_е) - это такое значение случайной величины, которое делит упорядоченную (в порядке возрастания или убывания величины) выборку пополам, то есть справа и слева от медианы находится равное количество значений случайной величины. При нечетном количестве измерений за медиану принимается непосредственно центральное значение, справа и слева от него располагается по (n-1)/2 значений. Так, в выборке из 15 упорядоченных значений это будет восьмое значение, а в выборке из 23 значений - двенадцатое и т.д.

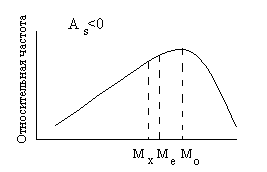
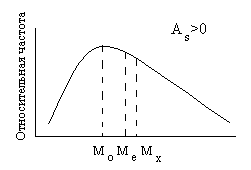
Рис.3. Соотношение между мерами центральной тенденции в асимметричном частотном распределении.

Если число значений случайной величины в выборке четное, то медиана оказывается между двумя значениями; в этом случае значение медианы рассчитывается как среднее между ними. На кривой распределения значение медианы всегда располагается между значениями моды и среднего арифметического (рис.3).

Квантили - это такие значения случайной величины, которые делят распределение на равные части. Есть несколько разновидностей квантилей:

• Квартили делят распределение на 4 равных части по 25%, соответственно квартилей три Q₁, Q₂, Q₃.

• Квинтили - их 4 (К₁ ....К₄), они делят распределение на 5 частей по 20% в каждой.

• Децили. Девять децилей (D₁ ... D₉) делят распределение на 10 частей по 10%.

• Процентили в количестве 99 (Р₁....Р₉₉) делят распределение на 100 частей по 1%.

Все остальные квантили можно выражать через процентили: так, первый квинтиль - это двадцатый процентиль или второй дециль. Второй квартиль - это 50 процентиль, или пятый дециль, или медиана.

Процентили нельзя ни в коем случае путать с процентными показателями. Процентные показатели - это первичные показатели, определяющие количество правильно выполненных заданий, а процентиль - показатель производный, указывающий на долю от общего числа членов группы. Первичный результат, который ниже любого показателя в выборке получает нулевой процентиль Р_о, а результат, превышающий все другие показатели группы - получает процентильный ранг 100 - Р₁₀₀. Эти процентили не означают ни нулевого, ни 100-процентного выполнения теста.

Среди характеристик рассеивания рассмотрим:

• размах d

• дисперсию ² или D

• среднеквадратическое (стандартное) отклонение 

• коэффициент вариации V.

Размах d - это разность между максимальным и минимальным значениями случайной величины:

d = х_max - х_min

Дисперсия 2 (или D) характеризует разброс значений случайной величины вокруг среднего арифметического значения, т.е. насколько плотно значения случайной величины группируются вокруг среднего арифметического Мх. Чем больше разброс, тем сильнее варьируют результаты испытуемых в данной группе, тем больше различия между испытуемыми.

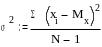
На первый взгляд может показаться, что было бы проще взять не квадрат значений отклонения от среднего, а просто отклонения значений от среднего. Но легко убедиться, что сумма таких отклонений будет равна нулю. Возведение же отклонений от среднего в квадрат позволяет избежать отрицательных чисел. На практике расчета дисперсии наряду с указанной формулой используется и расчет «способом моментов» по формуле

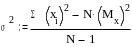
где (x_i)² - сумма квадратов значений Х.

Дисперсия имеет «квадратную размерность», то есть, если какая-то величина измерена в сантиметрах, то размерность дисперсии - сантиметры в квадрате, а если в баллах - то дисперсия - в «баллах в квадрате». Это не всегда удобно, большую наглядность в отношении разброса величины имеет среднеквадратическое или стандартное отклонение  (греческая буква «сигма»). Размерность этого параметра совпадает с размерностью случайной величины.

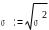
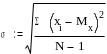
Среднеквадратическое отклонение используется очень широко в математической статистике. Малое значение стандартного отклонения указывает, что наблюдения хорошо группируются около среднего арифметического значения. Большое значение стандартного отклонения говорит о том, что наблюдения широко рассеяны относительно среднего значения и имеют слабую тенденцию к централизации.

Коэффициент вариации размерности не имеет, он служит для сравнения вариативности, то есть изменчивости случайных величин, имеющих различную природу. Рассчитывается коэффициент вариации по формуле:

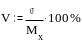
Если коэффициент вариации меньше 40%, то коэффициент вариации признается низким, то есть изменчивость величины невелика.

Характеристики асимметрии. В случаях, когда по тем или иным причинам более часто встречаются значения с показателями ниже или выше среднего, то появляются асимметричные распределения величины. Основная мера асимметрии - это коэффициент асимметрии A_s, рассчитываемый по формуле:

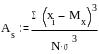
Коэффициент асимметрии изменяется от минус до плюс бесконечности. Асимметрия бывает левосторонняя или положительная, если A_s>0 (на рисунке 2 справа), и правосторонняя или отрицательная, если коэффициент асимметрии меньше 0 (слева на рис.2). При левосторонней асимметрии чаше встречаются значения по величине меньшие среднего арифметического (то есть медиана, и мода на графике находятся слева от среднего арифметического), при правосторонней асимметрии, соответственно, чаще встречаются значения, по величине превосходящие среднее арифметическое. Для симметричных распределений коэффициент асимметрии равен нулю, мода, медиана и среднее арифметическое совпадают между собой.

Характеристики эксцесса: Коэффициент эксцесса (или островершинности) рассчитывается по формуле

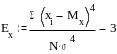
Распределения с острой вершиной будут характеризоваться положительным эксцессом, а сглаженные либо с понижением в центральной части - отрицательным. Пример расчета параметров распределения приведен в таблице 2:

Таблица 2

Расчет параметров распределения

Х	Отклонение от среднего (Xi - Mx)	(Xi - Mx) 2	(Xi - Mx) 3	(Xi - Mx) 4
48	8	64	512	4096
47	7	49	343	2401
43	3	9	27	81
41	1	1	1	1
41	1	1	1	1
40	0	0	0	0
38	-2	2	-8	16
36	-4	16	-64	256
34	-6	36	-216	1296
32	-8	64	-512	4096
Х=400 Mx=40		(Xi - Mx) 2 = =244	(Xi - Mx) 3=84	(Xi - Mx)4= =12244

Модальное значение - 41, поскольку оно встречается дважды. Медиана - 40.5 (пять чисел меньше этой величины, пять больше). Среднее арифметическое равно 400/10=40.

Дисперсия ² =244/9=27.11

Стандартное отклонение  =5.207.

Коэффициент асимметрии A_s = 0.011

Коэффициент эксцесса E_x = -1.334

При работе на компьютере параметры распределения можно рассчитать, используя встроенные функции Microsoft Excel. Для этого надо войти в раздел «Анализ данных» из меню «Сервис», где выбрать подраздел «Описательная статистика». На экране при этом высвечивается меню «Описательная статистика», в котором задаются входной интервал переменной и выходной интервал для вывода результатов расчета. Входной интервал переменной задается через двоеточие, например интервал «a1:a24» включает в себя 24 значения переменной в столбце A с 1 по 24 ячейку. Можно рассчитывать параметры распределения сразу нескольких переменных, если они представляют собой единый массив данных. Так, входной интервал a1:c25 включает в себя три переменных по 25 значений в каждой: a1:a25, b1:b25 и c1:c25. Если в первой строке интервала находится заголовок столбца (строки), то это следует указать в специальном окошке меню. В окне «Выходной интервал» следует указать номер левой верхней ячейки выходного интервала. Выходные данные включают среднее арифметическое значение, стандартную ошибку среднего, медиану, моду, стандартное отклонение, дисперсию выборки, коэффициенты эксцесса и асимметрии, размах выборки (обозначен как «Интервал»), минимальное и максимальное значения («Минимум» и «Максимум»), сумму всех значений и количество значений переменных («Счет»). Следует учесть, что в Microsoft Excel коэффициенты асимметрии и эксцесса рассчитываются по формулам, несколько отличающимся от приведенных выше.