7.2 Сравнение среднего значения некоторой выборки со средним значением генеральной совокупности или с нормативным значением

Для решения задачи такого рода используется один из вариантов t-критерия Стьюдента. Формула t-критерия в этом случае имеет следующий вид:

где М_х - среднее значение для исследуемой выборки,  - среднее значение для генеральной совокупности,  - стандартное отклонение и N - количество измерений в выборке. Число степеней свободы определяется по формуле  = N-1. Если t_эмп< t _кр, то принимается нулевая гипотеза об отсутствии значимых различий между средними арифметическими значениями выборки и генеральной совокупности, а если

t _эмп> t _кр, то принимается альтернативная гипотеза.

Задача: Для проверки знаний учащихся по иностранному языку использован специальный тест. Полученные нами результаты - 13, 17, 15, 23, 27, 29, 18, 27, 20, 24. Нормативное значение для данного теста составляет 18 баллов (данное значение является средним арифметическим значением генеральной совокупности, имеющей нормальное распределение). Можно ли признать выполнение теста группой в целом успешным?

Сумма значений выборки равна 213, среднее арифметическое 21.3, дисперсия D=30.46, стандартное отклонение =5.52. Проверяемая нулевая гипотеза Н₀ заключается в том, что среднее значение выборки значимо не выше нормативного. Альтернативная направленная гипотеза Н₁: количество баллов, набранных учащимися значимо выше нормативного.

Эмпирическое значение t-критерия равно

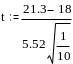
= 1.890

Полученный результат t=1.890 превышает табличное критическое значение, соответствующее 9 степеням свободы и =0.05 для одностороннего критерия (t_кр=1.83). Это значит, что мы можем принять альтернативную гипотезу и признать, что результаты выполнения теста группой выше нормативных.

Ответ: работу преподавателя английского можно признать успешной, поскольку результаты, показанные его учениками выше нормативных (=0.05).

7.3 Сравнение уровня признака в независимых выборках

Сравнение уровня признака в двух независимых выборках можно выполнить с помощью t-критерий Стьюдента (параметрический метод), либо с помощью критерия Манна-Уитни (непараметрический метод).

По t-критерию Стьюдента производится сравнение средних арифметических значений, то есть уровня признака, в двух независимых выборках с равной дисперсией и распределением случайной величины, соответствующим нормальному типу, Используется следующая формула t-критерия (здесь и ниже приводятся формулы критериев для малых выборок, то есть выборок с числом испытуемых менее 30):

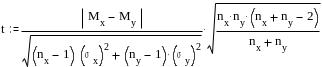
где n_x и n_y - количество испытуемых в 1 и 2 выборках, М_х и М_у - средние арифметические значения, _х и _у - стандартные отклонения соответственно в первой и второй выборках. Число степеней свободы  = n_x+ n_y - 2.

Равенство дисперсий проверяется по F-критерию Фишера:

F=₁²/₂²

За ₁² принимается большее из двух значений дисперсии, поэтому значение F_эмп. всегда больше 1. Полученное значение F_эмп сравнивается с критическим (Таблица 4 Приложения). При пользовании таблицей 4 ₁=n₁-1, ₂=n₂-1, критическое значение берется из клетки, находящейся на пересечении соответствующих строки и столбца. Если эмпирическое значение меньше критического, то различие дисперсий признается статистически незначимым.

Критическое значение t_кр определяется по таблицам (Таблица 5 Приложения) с учетом того, что критерий является двусторонним. Если t _эмп t _кр, то принимается альтернативная гипотеза.

В программе Microsoft Excel расчет эмпирического значения критерия Стьюдента выполняется с использованием встроенного «Двухвыборочного t-теста с одинаковыми дисперсиями». Для того чтобы воспользоваться встроенной функцией Microsoft Excel надо войти в раздел «Анализ данных» из меню «Сервис», где и выбрать «Двухвыборочный t-тест с одинаковыми дисперсиями». На экране высвечивается меню «Двухвыборочного t-теста с одинаковыми дисперсиями», в котором задаются интервалы обеих переменных, вероятность ошибки первого рода Альфа и выходной интервал (номер левой верхней ячейки выходного интервала). Входной интервал переменной задается через двоеточие, например интервал «a1:a24» включает в себя 24 значения переменной в столбце A с 1 по 24 ячейку. Если в первой строке интервала находится заголовок столбца (строки), то это следует указать в специальной ячейке меню. Гипотетическая средняя разность равна нулю по умолчанию. Выходные данные включают средние арифметические значения переменных в выборках, значения дисперсии, количество наблюдений в выборках, величину объединенной дисперсии, число степеней свободы, эмпирическое значение t-критерия и критические значения для одностороннего и двустороннего критериев.

Задача: В одной из школ Ленинградской области ученики 10 и 11 класса выполнили задания ШТУР (Школьный тест умственного развития). Различаются ли ученики 10 и 11 класса по уровню общей осведомленности?

Н₀: показатели осведомленности учеников 10 и 11 класса значимо не различаются.

Н₁: показатели осведомленности учеников 10 и 11 класса различаются значимо.

Таблица 10.

Сравнение показателей осведомленности по ШТУР учеников 10 и 11 классов одной из школ Ленинградской области (по t-критерию Стьюдента).
Результат ШТУР	z-оценка испытуемого	fэмп. по интервалам z		Результат ШТУР	z-оценка испытуемого	fэмп. по интервалам z
20	1,369194			20	1,632993
20	1,369194			18	1,020621
19	1,039268			18	1,020621	3
19	1,039268	4		17	0,714435
18	0,709341			17	0,714435
18	0,709341			16	0,408248
18	0,709341			16	0,408248	4
18	0,709341			15	0,102062
17	0,379415			15	0,102062
17	0,379415	6		14	-0,20412	3
16	0,049489	1		13	-0,51031	1
15	-0,28044			11	-1,12268
14	-0,61036			11	-1,12268
14	-0,61036			10	-1,42887
14	-0,61036			9	-1,73506	4
14	-0,61036	5
13	-0,94029
13	-0,94029
10	-1,93007
10	-1,93007	4
Среднее арифметическое Мх=15.85 Дисперсия 2=9,19 Стандартное отклонение  =3,031				Среднее арифметическое Мх=14,67 Дисперсия 2=10,67 Стандартное отклонение  =3,266
Проверка распределений результатов ШТУР на соответствие нормальному распределению:
2эмпир.= (4-4.00)2 + (6-4.00)2 +(1-4.00)2 + (5-4.00)2 + 4.00 4.00 4.00 4.00 + (4-4.00)2 = 3.50 4.00 2эмпир.(3.50) < 2кр.(5.99), следовательно, распределение не отличается значимо от нормального (=0.05), и к нему могут быть применены параметрические критерии.				2эмпир.= (3-3.00)2 + (4-3.00)2 +(3-3.00)2 +(1-3.00)2+ 3.00 3.00 3.00 3.00 + (4-3.00)2 = 2.00 3.00 2эмпир.(2.00) < 2кр.(5.99), следовательно, распределение не отличается значимо от нормального (=0.05), и к нему могут быть применены параметрические критерии.
Проверка равенства дисперсий: Fэмп=10.67/9.19=1.161. Fкр.=2.32 при =0.05 Fэмп<Fкр.  может быть использован критерий Стьюдента для двух выборок с равными дисперсиями.
			= 1.106 =33. tкр.= 2.03 (=0.05)
t эмп. < t кр.  принимается нулевая гипотеза Н0. Ответ: уровень осведомленности учеников 11 класса не отличается значимо от такового у учеников 10 класса (=0.05).

Применение критерия Стьюдента связано с целым рядом ограничений - соответствие обоих распределений нормальному типу, равенство дисперсий распределений, достаточные объемы выборок. Если для решения поставленной задачи использовать параметрический критерий Стьюдента нельзя, то следует воспользоваться его непараметрическим аналогом - критерием Манна-Уитни. Для применения непараметрического критерия Манна-Уитни требуется лишь, чтобы оба распределения относились к сходному, а не обязательно к нормальному типу, кроме того, признак может быть измерен не только в шкале отношений или интервалов, но и в шкале рангов.

Что особенно ценно, критерий Манна-Уитни применим при малых количествах наблюдений в выборках: в каждой выборке должно быть не менее 3 наблюдений. Допускается также, чтобы в одной из выборок было 2 наблюдения, но при этом в другой их должно быть не менее 5. Максимальное число наблюдений в выборках 60, для большего числа наблюдений нет таблиц критических значений. Но уже когда число наблюдений свыше 20 в каждой выборке, расчет критерия становится достаточно трудоемким для расчетов на калькуляторе.

Порядок действий при расчете эмпирического значения критерия следующий:

1. Проранжировать все измерения, объединив результаты двух выборок. Правила ранжирования следующие:

• Наименьшему значению из всех присваивается ранг 1, наибольшему - n₁+n₂.

• Если два или большее количество значений равны, то для них рассчитывается средний ранг. Например, если три наименьших значения в выборке равны, то их средний ранг был бы (1+2+3)/3=2. А если равны 10 и 11 значения, то их средний ранг (10+11)/2=10.5.

2. Подсчитать сумму рангов отдельно для первой (R₁) и для второй (R₂) выборки. Проверить, совпадает ли общая сумма рангов с расчетной по формуле R₁+R₂=N(N+1)/2, где N= n₁+n₂ - общее число ранжируемых значений.

3. Рассчитать эмпирические значения критерия Манна-Уитни для выборок:

U₁= n₁^.n₂+ n₁ (n₁+1)/2 - R₁

U₂ = n₁^.n₂ + n₂(n₂+1)/2 - R₂

4. Проверить правильность расчета с помощью выражения U₁+U₂= n₁^.n₂.

5. Эмпирическим значением является меньшее из двух рассчитанных значений. Оно сопоставляется с критическими значениями, приведенными в таблице 6 Приложения для =0.05 и =0.01. Чем меньше значение U, тем выше достоверность различий, а значит, если U_эмпU_крит, то принимается нулевая гипотеза Н₀, если U_эмп<U_крит, то принимается альтернативная гипотеза.

Задача: В одной из школ Ленинградской области ученики 10 и 11 класса выполнили задания ШТУР (Школьный тест умственного развития).

Результаты тестирования

10 класс: 20, 21, 20, 14, 14, 20, 11, 17, 14, 15, 10, 6, 7, 10, 10.

11 класс: 23, 23, 20, 23, 23, 20, 22, 21, 19, 16, 15, 14, 17, 21, 16, 14, 13, 12, 12, 16.

Различаются ли ученики 10 и 11 класса по способности классификации?

Н0: способности классификации учеников 10 и 11 класса значимо не различается.

Н1: показатели способности классификации учеников 10 и 11 класса различаются значимо.

Таблица 11

Сравнение способности классификации по результатам ШТУР у юношей – учеников 10 и 11 классов (по критерию Манна-Уитни)
10 класс		11 класс
Исходные данные	Ранг	Исходные данные	Ранг
6	1
7	2
10	4
10	4
10	4
11	6
		12	7,5
		12	7,5
		13	9
14	12
14	12
14	12
		14	12
		14	12
15	15,5
		15	15,5
		16	18
		16	18
		16	18
		17	20,5
17	20,5
		19	22
20	25
20	25
20	25
		20	25
		20	25
21	29
		21	29
		21	29
		22	31
		23	33,5
		23	33,5
		23	33,5
		23	33,5
Сумма	197		433
Проверка: Общая сумма рангов 197+433=630. N (N+1)/2=35х36.3=630, т.е. ранжирование выполнено верно. U1=20х15+15x16/8-197=223 U2=20x15+20х21/2-433=77 Проверка: U1+U2=300. n1x n2=300
Uэмп. = 77; Uкр.= 80. Uэмп.< Uкр. принимается альтернативная гипотеза Н1 . Ответ: способность к классификации (по результатам ШТУР) у учеников 11 класса отличается значимо от таковой у учеников 10 класса.

Иногда исследователю приходится сравнивать не две, а несколько выборок: три, четыре и более. В таких случаях возможно попарное сравнение всех выборок по критерию Стьюдента или Манна-Уитни, но быстрее и проще использовать достаточно простой непараметрический критерий, представляющий собой одну из модификаций критерия Вилкоксона - Т-критерий Вилкоксона для множественных сравнений. Критерий может использоваться при количестве условий (то есть сравниваемых выборок) от 3 до 10, количество испытуемых в каждой выборке от 3 до 25. Важно, чтобы выборки были равными по численности. Если исходные выборки различаются по численности, то их следует уравнять, отбросив случайным образом из больших по объему выборок «лишние» значения.

Порядок расчета эмпирического значения критерия следующий:

1. Проранжировать все измерения, объединив результаты выборок. Наименьшему значению из всех присваивается ранг 1, наибольшему - N = n₁+n₂+.... Если два или большее количество значений равны, то для них рассчитывается средний ранг, как это делали, рассматривая критерий Манна-Уитни.

2. Подсчитать сумму рангов отдельно для первой (R₁), второй (R₂) третьей (R₃) и других выборок. Проверить, совпадает ли общая сумма рангов с расчетной по формуле R₁+R₂+R₃+ +...=N(N+1)/2, где N= n₁+n₂+n₃+... - общее число ранжируемых значений.

3. Рассчитать эмпирические значения критерия Вилкоксона для множественных значений. За эмпирические значения принимаются разности сумм рангов между всеми выборками попарно. Результаты удобно представить в виде матрицы. В заголовках строк и столбцов такой матрицы находятся названия выборок и суммы рангов для каждой из них, а на пересечении строк и столбцов матрицы указываются абсолютные значения разностей, показывающие, насколько отличаются суммы рангов соответствующих выборок. Матрица получается симметричной относительно главной диагонали, в ячейки главной диагонали нули можно не записывать.

4. Сравнить эмпирические значения критерия с критическими, приведенными в соответствующей таблице (Таблица 7 Приложения). Если эмпирическое значение больше ли равно критическому, то принимается альтернативная гипотеза, если меньше - то нулевая.

Задача: В одной из школ Ленинградской области ученики 10 и 11 класса выполнили задания ШТУР (Школьный тест умственного развития). Различаются ли ученики - юноши и девушки из 10 и 11 классов по уровню общей осведомленности?

Н0: уровень общей осведомленности у юношей и девушек из 10 и 11 классов значимо не различается.

Н1: показатели уровня общей осведомленности у юношей и девушек из 10 и 11 классов различаются значимо.

Таблица 12

Сравнение уровня общей осведомленности юношей и девушек 10 и 11 классов одной из школ Ленинградской области (По критерию Вилкоксона для множественных сравнений)
Юноши, 11 класс*		Девушки, 11 класс*		Юноши, 10 класс		Девушки, 10 класс*
Общая осведомленность	Ранг	Общая осведомленность	Ранг	Общая осведомленность	Ранг	Общая осведомленность	Ранг
18	49	17	42,5	19	55	5	1,5
15	33,5	13	23,5	17	42,5	7	4,5
10	13	13	23,5	16	37,5	8	6,5
17	42,5	15	33,5	17	42,5	9	9
17	42,5	19	55	17	42,5	10	13
15	33,5	12	19,5	19	55	10	13
12	19,5	19	55	16	37,5	10	13
20	59,5	19	55	12	19,5	11	16,5
11	16,5	17	42,5	14	28	13	23,5
20	59,5	15	33,5	10	13	14	28
14	28	9	9	9	9	14	28
19	55	19	55	7	4,5	14	28
17	42,5	13	23,5	12	19,5	15	33,5
18	49	15	23,5	6	3	18	49
18	49	8	6,5	5	1,5	18	49
Ме=17 q=2		Ме=15 q=3		Ме=14 q=4		Ме=11 q=2.5
Суммы рангов по группам:	592,5		501		410,5		316

* - для данных групп использованы случайные выборки по 15 человек из имеющихся результатов ШТУР.

Таблица 13

Эмпирические значения Т (Тэмп=Ra-Rb)
	Юноши, 11 класс	Девушки, 11 класс	Юноши, 10 класс	Девушки, 10 класс
Юноши, 11 класс	0	91,5	182	276,5
Девушки, 11 класс	91,5	0	90,5	185
Юноши, 10 класс	182	90,5	0	94,5
Девушки, 10 класс	276,5	185	94,5	0

Tкр.=246 (=0.05)

Т эмп > Tкр только в одном случае (девушки 10 класса и юноши 11 класса).

Ответ: различия в уровне общей осведомленности значимы между девушками 10 класса и юношами 11 класса (=0.05).