3. Случайная величина

3.1 Распределение случайной величины

Случайной величиной называется такая переменная величина, которая принимает значения из некоторого множества. Принято выделять дискретные и непрерывные случайные величины. Дискретная случайная величина принимает свои значения из множества целых чисел - например, количество учеников в классе, количество несчастных случаев на производстве и так далее. Непрерывная случайная величина принимает свои значения из множества действительных чисел. Ряд психологических явлений непрерывен по своей природе. Это относится, например, к интеллекту, эмоциональности, тревожности, воображению и т.д. Чтобы описать и измерить такие явления, мы разбиваем числовую ось на равные интервалы. Например, возраст мы измеряем, как правило, интервалами, равными одному году. Время принято измерять интервалами, равными секунде, минуте, часу, суткам и т.д. Операция разбиения числовой оси на равные интервалы называется квантованием, а полученные интервалы - интервалами квантования.

Основной способ описания случайной величины - построение ее распределения. Для дискретной величины подсчитывают количество случаев, приходящихся на каждое значение (абсолютная частота), и затем строят гистограмму (столбчатую диаграмму), наглядно представляющую особенности распределения. На гистограмме по оси «Х» откладывается значение случайной величины, а по оси «Y» - абсолютная частота (Рис.1).

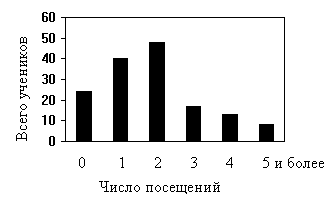
Рис 1. Гистограмма распределения количества посещений медицинского кабинета учениками школы в течение учебного года.

Для описания непрерывной случайной величины либо большого количества измерений дискретной случайной величины данные предварительно следует сгруппировать по интервалам квантования. Прежде всего, надо составить таблицу частотного распределения. Данные группируются по интервалам квантования, и подсчитывается число попаданий в каждый из интервалов. Полученное таким образом число (количество случаев) и есть частота соответствующего интервала. Сумма всех частот интервалов равняется N, то есть общему числу случаев. Отношение частоты к общему числу случаев называется относительной частотой интервала (Таблица 1).

Пример: Результаты тестирования 14 учеников учеников 10 класса одной из школ Ленинградской области (по результатам ШТУР субтест: способность обобщения):

7; 10; 11; 11; 12; 13; 13; 14; 16; 16; 18; 18; 20; 25; 28.

Таблица 1

Способность обобщения учеников 10 класса одной из школ Ленинградской области (по результатам штур)

Вариант А				Вариант Б
Интервал квантования	Абсолютная частота	Относительная частота (%)	Интервал квантования		Абсолютная частота	Относительная частота (%)
[6 - 8]	1	7	[6-10]		2	13
[9 - 11]	3	20	[11-15]		6	40
[12-14]	4	26	[16-20]		5	33
[15-17]	2	13	[21-25]		1	7
[18-20]	3	20	[26-30]		1	7
[21-23]	0	0
[24-26]	1	7
[27-29]	1	7

На практике наиболее удобно, чтобы количество интервалов (столбцов) было не меньше 5, но не больше 15. Формировать интервалы можно различным образом, начиная либо с наименьшей, либо наибольшей величины, важно, чтобы расстояние между границами интервалов было одинаковым. При подготовке данных для построения гистограммы рекомендуется не ограничиваться лишь одной попыткой квантования: нередко изменение числа групп и границ интервалов помогает выявить скрытые неоднородности распределения случайной величины (рис.1).

Подсчитав частоту для каждого интервала, строим гистограмму. Чтобы подчеркнуть непрерывность изменения случайной величины, столбцы гистограммы следует располагать вплотную друг к другу. На оси «Х» графика принято обозначать или границы, или середины интервалов квантования. По оси «Y» указывается абсолютная частота. Результаты построения можно представить не только в виде столбчатой диаграммы, но также в виде полигона. На полигоне частот число испытуемых указывается точкой, расположенной над серединой интервала на высоте, соответствующей его частоте, а сами точки последовательно соединены прямолинейными отрезками (рис.2). Полигон по своему назначению полностью аналогичен гистограмме.

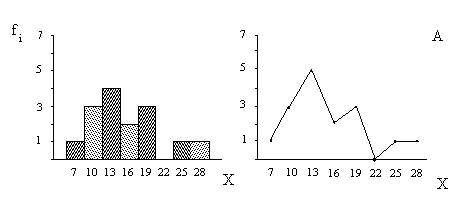
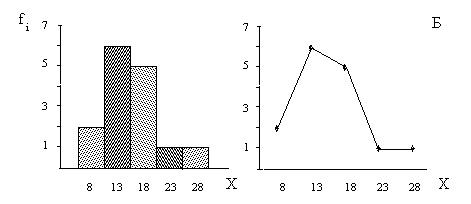
Рис. 2. Гистограмма (слева) и полигон распределения случайной величины (способности обобщения) по данным таблицы 1, с выделением 8 (А) и 5 (Б) интервалов квантования. По оси Х указаны середины интервалов.

При характеристике распределения некоторой непрерывной случайной величины число подразделений по горизонтальной шкале теоретически является бесконечным, а значение каждого интервала - бесконечно малым. В этом случае полигон частот примет вид кривой распределения частоты встречаемости случайной величины.