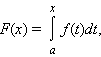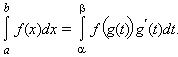6.Правила интегрирования.

1)∫d(f(x))=f(x)+C;

2)d∫f(x)dx=f(x)dx;

3)∫kf(x)dx=kf(x)dx, где k — постоянная величина;

4)∫(f(x))±g(x))dx=∫f(x)dx±∫g(x)dx;

5)∫udv=uv-∫vdu (интегрирование по частям);

6)∫f(x)dx=F(x)+C ∫f(φ(t))φ`(t)dt=F(φ(t))+C (замена переменной интегрирования);

^{7) ∫f(x)dx=F(x)+C ∫ f(ax+b)dx=1/a F(ax+b)+C.}

7. Таблица неопределенных интегралов

• ∫xⁿdx=xⁿ⁺¹/(n+1)+C,n -1

• ∫dx/x=lnІxІ+C

• ∫a^xdx =a^x/lna + C

• ∫e^xdx=e^x+C

• ∫sinxdx=-cosx +C

• ∫cosxdx=sinx +C

• ∫dx/cos²x=tgx+C

• ∫dx/sin²x=-ctgx +C

• ∫dx/(1+x²)=arctgx+C

• или ∫dx/(1+x²) =-arcctgx+C

• ∫dx/ = arcsinx +С

• или ∫dx/ =-arccosx + C

• ∫dx/(a²+x²)= arctg +C

• ∫dx/(a²+x²)=- arcctg +C

• ∫dx/ =arcsin +C (a>0)

• ∫ dx/ =-arccos +C (a>0)

• ^∫ dx/ =lnІx+ І+C

5. Таблица производных

8. ДОПОЛНИТЕЛЬНЫЙ

Формула Ньютона-Лейбница

Если непрерывна на отрезке и  — ее любая первообразная на этом отрезке, то имеет место равенство

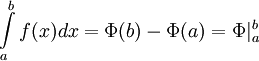
ЭТО ЕСЛИ ВСЕ РАСПИСАТЬ:

Если функция f (x) интегрируема на [a; b], то для любого существует интеграл

который называется интегралом с переменным верхним пределом.

Если функция f интегрируема на [a; b], то функция F (x) непрерывна на этом отрезке.

Если функция f интегрируема на [a; b] и непрерывна в то функция F (x) дифференцируема в  причем

Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида

где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле.

 

Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:

Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда

Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).

Пусть f (x) непрерывна на [a; b], g (t) имеет непрерывную производную на [α; β], Тогда если a = g (α), b = g (β), то справедлива формула замены переменной в определенном интеграле:

Если функции u (x) и v (x) имеют на [a; b] непрерывные производные, то справедлива формула интегрирования по частям:

9.Эллипс(основной 11)

10

a-действительная полуось,b-мнимая полуось,расстояние от центра до фокусов c=a²+b²,эксцентриситет ε=c/a>1

12)Гипербола

X

=1

² _ Y²

a ² b²

=1 a-мнимая полуось ,b- действительная полуось, расстояние от центра до фокусов c=a²+b² ,эксцентриситет ε=с/b>1

y² x²

b² a²

Линиями второго порядка называются линии, уравнения которых имеют вторую степень.

11.Парабола

Параболой называется множество всех точек равноудалённых от данной точки (фокуса) и от данной прямой (директрисы).

Парабола у =2рх (р>0)

р - расстояние между фокусом и директрисой