1. Определители и их свойства

Для квадратной матрицы можно вычислить число, которое называется определителем. Определитель второго порядка вычисляется по схеме «крест», а третьего порядка – по схеме треугольников.

Будем рассматривать квадратные матрицы

Определители являются основными числовыми характеристиками квадратных матриц.

 Определителем (детерминантом) матрицы ,

 состоящей из одного числа  , называется само это число.

Определителем матрицы А=  второго порядка называется число, равное разности произведений элементов главной и побочной диагоналей:

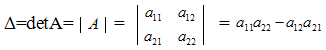
Рассмотрим матрицу третьего порядка:

Определителем матрицы A третьего порядка называется число

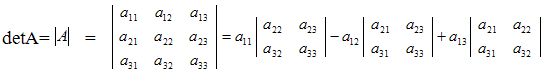
Данная формула называется формулой разложения определителя 3 порядка по элементам первой строки.

1. Определитель транспонированной матрицы равен определителю исходной матрицы.

2. Если в определителе какие-либо  две строки (столбца) равны между собой, то такой определитель равен 0.

3. Общий множитель всех элементов какой-либо строки (или столбца) можно выносить за знак определителя.

4. Если поменять в определителе местами какие-либо две строки (столбца), то определитель меняет знак.

5. Если все элементы какой-либо строки (столбца) определителя равны 0, то такой определитель равен 0.

6. Если к элементам какой-либо строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца) этого же определителя, умноженные на одно и то же число, то определитель не изменяется.

2. Решение систем линейных уравнений с помощью определителей

I. Система двух линейных уравнений с двумя неизвестными

Систем двух линейных уравнений с двумя неизвестными имеет вид

     (4)

Определителем этой системы называется определитель, составленный из коэффициентов при неизвестных. Этот определитель

     (5)

будем обозначать буквой D.

1. Если определитель системы не равен нулю, то система (4) имеет единственное решение, которое находится по формулам

     (6)

В этом случае говорят, что система - совместная или определенная. Определители, стоящие в числителях этих дробей, будем обозначать соответственно через D_x и D_y.

Итак, значение неизвестного системы (4) равно дроби, знаменатель которой есть определитель системы, а числитель есть определитель, получающийся из определителя системы заменой в нем столбца из коэффициентов при определяемом неизвестном столбцом свободных членов.

2. Если же определитель системы D равен нулю, но, по крайней мере, один из определителей D_x и D_y в числителях формул (6) не равен нулю, то система решений не имеет. В этом случае говорят, что она противоречива, или несовместна.

3. Если же равен нулю не только определитель системы, но и определители D_x и D_y, а хотя бы один из коэффициентов при неизвестных не равен нулю, то одно из уравнений системы является следствием другого, и система (4) двух линейных уравнений с двумя неизвестными приводится к одному уравнению, всякое решение которого является одновременно и решением второго уравнения. В этом случае система допускает бесконечное множество решений, и о ней говорят, что она неопределенная.