II. Система трех линейных уравнений с тремя неизвестными

Система трех линейных уравнений с тремя неизвестными имеет вид

     (7)

Определитель

     (8)

составленный из коэффициентов при неизвестных, называется определителем системы.

1. Если определитель системы , то система (7) имеет решение, и притом единственное. Это решение находится по формулам

     (9)

Из этого заключаем, что значение неизвестного системы (7) равно дроби, знаменатель которой есть определитель системы, а числитель есть определитель, получающийся из определителя системы заменой в нем столбца из коэффициентов при определяемом неизвестном столбцом свободных членов.

Определители, стоящие в числителях дробей (9), будем обозначать соответственно через D_x, D_y, D_z.

2. Если D = 0, но, по крайней мере, один из его миноров и хотя бы один из определителей D_x, D_y и D_z не равен нулю, то система (7) решений не имеет. В этом случае говорят, что она противоречива, или несовместна.

3. Если D = 0 и все определители, стоящие в числителях дробей (9), - D_x, D_y, D_z - равны нулю, т. е. если

D = D_x = D_y = D_z = 0,

но хотя бы один из миноров в определителе D не равен нулю, то одно уравнение системы (7) является следствием двух других, и система трех уравнений (9) приводится к двум уравнениям, причем решения этих двух уравнений удовлетворяют третьему. В этом случае система (9) имеет бесконечное множество решений и называется неопределенной.

4. Если же все миноры в определителе D равны нулю, но хотя бы один из миноров в каком-нибудь из определителей D_x, D_y, D_z не равен нулю и хотя бы один из коэффициентов при неизвестных не равен нулю, то система несовместна и решений не имеет.

5. Если в определителях D, D_x, D_y, D_z все миноры равны нулю, но хотя бы один из коэффициентов при неизвестных нулю не равен, то два уравнения системы являются следствием третьего, и система трех уравнений приводится к одному уравнению, является неопределенной и имеет бесконечное множество решений, причем решения этого третьего уравнения удовлетворяют первому и второму уравнениям.

3.Линейные операции с векторами на плоскости и в пространстве.

Линейными операциями над векторам называются операции сложения векторов и умножения вектора на число.

Системы координат на плоскости и в пространстве

Прямолинейной системой координат на плоскости называется сово­купность двух числовых осей с общим началом. Если масштабы на осях равны и оси перпендикулярны, то система координат называется прямоугольной декартовой. Обычно используется правая прямоугольная декартова система координат. Любая точка на плоскости однозначно определяется парой своих координат, и наоборот: любая пара действительных чисел задает единственную точку на плоскости.

Прямолинейной системой координат в пространстве называется сово­купность трех числовых осей с общим началом, не лежащих в одной плоскости. Если масштабы на осях равны и оси перпендикулярны, то система координат называется прямоугольной декартовой. Обычно используется правая прямоугольная декартовая система координат. Любая точка в пространстве однозначно определяется тройкой своих координат, и наоборот: любая тройка действительных чисел задает единственную точку в пространстве.

Пусть даны две точки на плоскости А(х₁у1) и В(х₂,у2). Тогда расстоя­ние между ними вычисляется по формуле d=√(x2 –x1)²+(У2 –У1)² . Ана­логично для двух точек в пространстве А(х1у1) и В(х₂,у2) расстояние между ними вычисляется по формуле d=√(х₂ –х1)^² +(у₂ –у1)^² +(z₂ –z1)^² -

Векторы и линейные операции над ними _ _

Вектором называется направленный отрезок. Обозначаются векторы тремя способами: а, или а, или АВ. Два вектора равны, если их длины равны и они однонаправленны. Три вектора а Ь и с в пространстве назы­ваются компланарными, если они параллельны одной плоскости. Координаты вектора равны разности координат конца и начала. Сумма и разность векторов определяются по правилу треугольника:

Произведением вектора а на число λ называется вектор, длина которо­го равна |λ||а|; он однонаправлен с исходным, если λ>0, и противоположно направлен, если λ<0. Из определения суммы следуют правило параллелограмма для суммы двух векторов и правило многоугольника для суммы нескольких векторов:

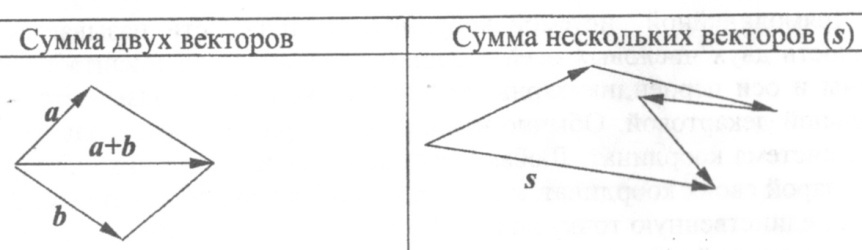
Если даны координаты векторов, то координаты суммы равны сумме ко­ординат, координаты разности равны разности координат, а координаты про­изведения вектора на число равны произведению координат на это число.