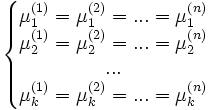26.Фазовое равновесие: твердое тело — пар.

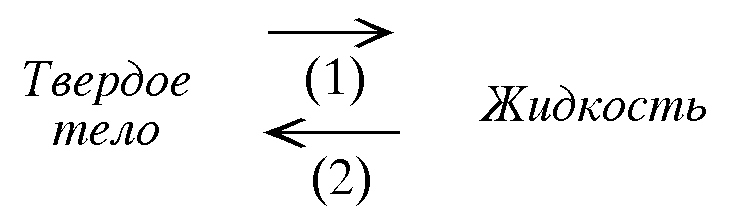
Процесс (1) называется сублимация или возгонка. А процесс (2) — конденсация. Для многих твердых веществ давление насыщенного пара очень мало. Основное условие измерения давления насыщенного пара твердого тела: в системе должно быть только твердое тело и его пар.

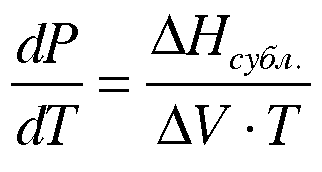- уравнение Клапейрона-Клаузиуса для данного случая.

По закону Гесса : ΔН_су6л=ΔН_плавл + ΔН_исп, — данное равенство соблюдается точно, когда в равновесии находятся все три фазы. Примем три допущения для решения уравнения Клаузиуса-Клайперона:

4)

5)В узком температурном интервале тепловой эффект испарения не зависит от температуры;

6) Считаем пар идеальным газом, для 1 моля которого выполняется закон Менделеева-Клайперона Тогда, учитывая допущения, уравнение Клаузиуса-Клайперона примет вид:

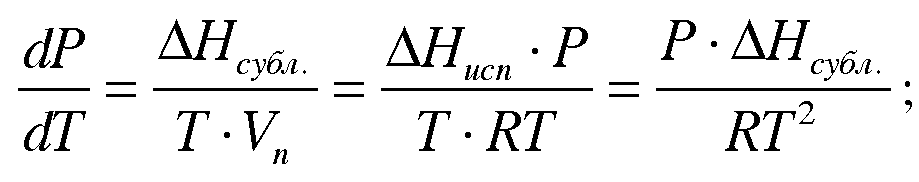
Таким образом экспериментально можно определить теплоту сублимации. разделим переменные:

27. Правило фаз Гиббса. Диаграмма состояния однокомпонентной системы.

Компонентом называется химически однородная составная часть вещества, которая может быть выведена из системы. Диаграммами состояния (фазовыми диаграммами) называются диаграммы, по которым можно определить условия устойчивости фаз и фазового равновесия. В качестве примера диаграммы состояния однокомпонентной системы рассмотрим диаграмму состояния воды. Каждая точка поля диаграммы состояний характеризуется парой чисел P и Т. AO - зависимость давления насыщенного пара твердого тела от температуры OD- зависимость

OB -

AO - равновесие тв.тело пар

OD - равновесие жидкость пар

OB - равновесие тв.тело жидкость

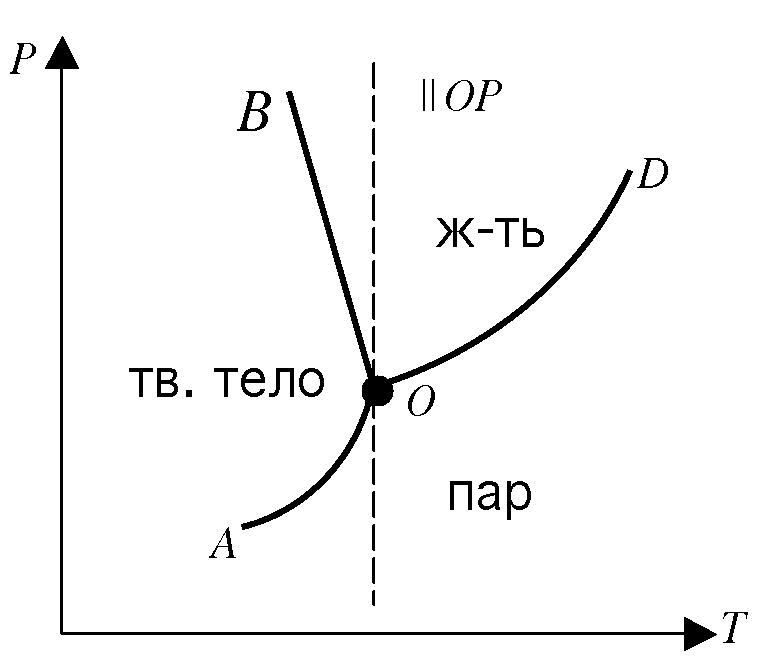
Во всех других точках диаграммы состояний, которые не лежат на перечисленных

кривых, система существует в виде одной фазы. В точке О в равновесии существуют все три фазы. Эта точка называется тройной. Обозначим через Ф - число фаз системы. Пусть / - число степеней свободы, то есть число параметров, которые можно менять, не меняя состояния системы. К - число независимых компонентов системы. Также через п обозначим число внешних условий, влияющих на равновесие (как правило, давление и температура, т.е. п = 2 ). Правило фаз Гиббса:

Условие равновесия фаз

Рассмотрим химически однородную систему (состоящую из частиц одного типа). Пусть в этой системе имеется граница раздела между фазами 1 и 2. Как было указано выше, для равновесия фаз требуется равенство температур и давлений на границе раздела фаз. Известно (см. статью Термодинамические потенциалы), что состояние термодинамического равновесия в системе с постоянными температурой и давлением соответствует точке минимума потенциала Гиббса.

Потенциал Гиббса такой системы будет равен

• ,

где μ₁ и μ₂ — химические потенциалы, а N₁ и N₂ — числа частиц в первой и второй фазах соответственно.

При этом сумма N = N₁ + N₂ (полное число частиц в системе) меняться не может, поэтому можно записать

• .

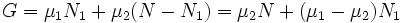Предположим, что , для определенности, . Тогда, очевидно, минимум потенциала Гиббса достигается при (все вещество перешло в первую фазу).

Таким образом, равновесие фаз возможно только в том случае, когда химические потенциалы этих фаз по разные стороны границы раздела равны:

• .

Правило фаз Гиббса

Рассмотрим теперь систему, вообще говоря, химически неоднородную (состоящую из нескольких веществ). Пусть k — число компонентов (веществ) в системе, а n — число фаз. Условие равновесия фаз для такой системы можно записать в виде системы из k(n − 1) уравнений:

• 

Здесь — химический потенциал для i-го компонента в j-й фазе. Он однозначно определяется давлением, температурой и концентрацией каждого компонента в фазе. Концентрации компонетнов не независимы (их сумма равна 1). Поэтому рассматриваемая система уравнений содержит неизвестных (n(k − 1) — концентрации компонентов в фазах, плюс температура и давление).

Система разрешима, вообще говоря, если число уравнений не превышает числа неизвестных (система, не удовлетворяющая этому условию, также может быть разрешима, однако это исключительный случай, с которым в физике можно не считаться). Поэтому

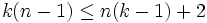• отсюда ,

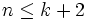то есть число фаз в равновесной системе может превышать число компонентов не более, чем на два.

Последнее неравенство называется правилом фаз Гиббса. В частном случае для однокомпонентной (химически однородной системы) оно превращается в условие

• .

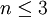Диаграммы однокомпонентных систем

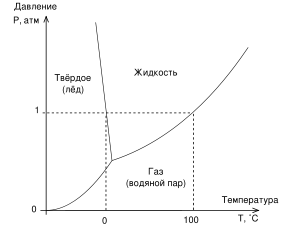
Фазовая диаграмма воды

На фазовых диаграммах однокомпонентных систем поля, по правилу фаз, соответствуют однофазным состояниям, линии, разграничивающие их - двухфазным, точки пересечения линий - трёхфазным (эти точки называют тройными точками).

Двухфазные линии, как правило, либо соединяют две тройные точки, либо тройную точку с точкой на оси ординат, отвечающую нулевому давлению. Исключение составляет линия жидкость-газ, заканчивающаяся в критической точке. При температурах выше критической различие между жидкостью и паром исчезает.