
Линейные преобразования случайных процессов
Перечислить основные виды сходимости случайных величин.
1)С вероятностью 1
2) По вероятности
3) Среднеквадратичная сходимость
4) По расприделению.
Дать определение непрерывности случайного процесса по вероятности.
CП
называется
непрерывным по вероятности в точке
![]() если
если
![]()
Дать определение сходимости в среднеквадратическом.
![]()
Сформулировать критерий сходимости Лоэва.
![]()
Дать определение непрерывности случайного процесса в среднеквадратическом.
CП называется непрерывным в среднеквадратическом в точке
![]()
Сформулировать условие непрерывности случайного процесса в терминах ковариационной функции.
![]()
Сформулировать условие непрерывности случайного процесса в терминах математического ожидания и корреляционной функции.
Сформулировать условие непрерывности стационарного случайного процесса.
Если
ССП то
![]() должен быть непрерывный в точке
должен быть непрерывный в точке
![]() 0
0
Как связаны непрерывности по вероятности и в среднеквадратическом?
Означает ли непрерывность случайного процесса непрерывность его реализаций? Пояснить.
Из непрерывности СП не следует непрерывность его реализаций. На реализациях могут быть разрывы 1 рода, которые не влияют на непрерывность.
Определение производной случайного процесса.
-
непрерывный СП
![]()
Сформулировать условия существования производной случайного процесса в терминах ковариационной функции.
![]()
Сформулировать условия существования производной случайного процесса в терминах математического ожидания и корреляционной функции.
1)
![]()
Сформулировать условия существования производной стационарного случайного процесса.
Должна сушествовать
![]()
Сформулировать условия существования
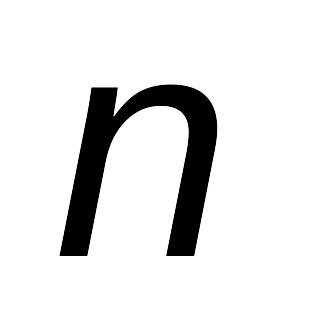 -той
производной случайного процесса в
терминах ковариационной функции.
-той
производной случайного процесса в
терминах ковариационной функции.
![]()
Сформулировать условия существования -той производной случайного процесса в терминах математического ожидания и корреляционной функции.
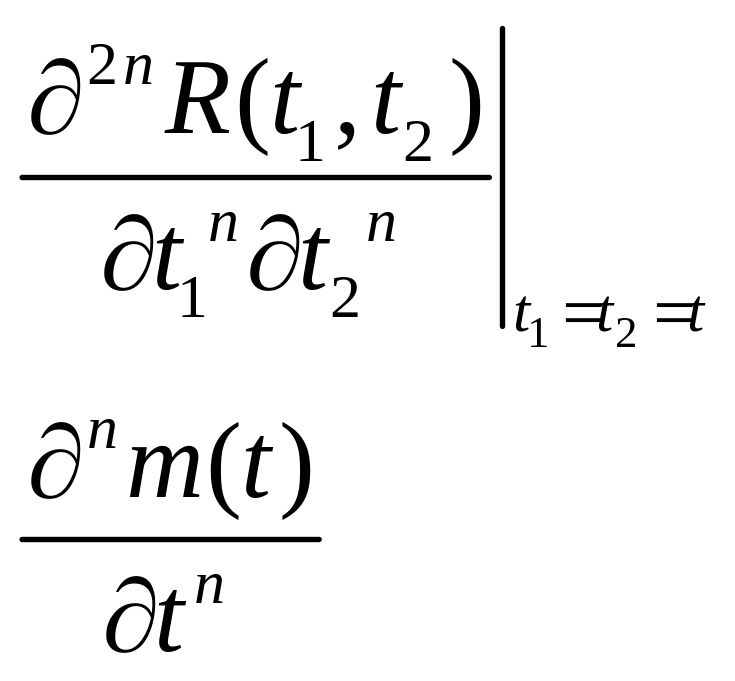
Сформулировать условия существования -той производной стационарного случайного процесса.
Чему равно математическое ожидание производной случайного процесса? Доказать.
![]()
Чему равно математическое ожидание производной стационарного случайного процесса? Доказать.
![]()
Чему равна корреляционная функция производной случайного процесса? Доказать.
![]()
Чему равна корреляционная функция производной стационарного случайного процесса? Доказать.
![]()
Чему равна взаимная корреляционная функция случайного процесса и его производной? Доказать.
![]()
Чему равна взаимная корреляционная функция стационарного случайного процесса и его производной? Доказать.
![]()
Чему равна взаимная корреляционная функция производной и случайного процесса? Доказать.
![]()
Чему равна взаимная корреляционная функция производной и стационарного случайного процесса? Доказать.
![]()
Являются ли некоррелированными стационарный случайный процесс и его производная в одинаковые моменты времени? Ответ обосновать.
Да являются. Так как производная от корреляционной фун. Непарная и семерична от 0, и возможен только такой вариант когда она через него проходит то в нуле всегда будет 0. Что означает что они некорелированны.
Чему равно математическое ожидание отклика линейной системы при воздействии случайного процесса?
Чему равна корреляционная функция отклика линейной системы?
Чему равна дисперсия отклика линейной системы?
Как найти взаимную корреляционную функцию между воздействием и откликом линейной системы?
Чему равна корреляционная функция отклика непараметрической линейной системы при воздействии стационарного случайного процесса?
Чему равно математическое ожидание отклика непараметрической линейной системы при воздействии стационарного случайного процесса?
Что такое корреляционное преобразование импульсной характеристики линейной системы?
![]()
Как найти дисперсию отклика непараметрической линейной системы при воздействии стационарного случайного процесса?
Чему равна взаимная корреляционная функция между воздействием и откликом непараметрической линейной системы, если воздействие — стационарный случайный процесс?
![]()
Чему равна корреляционная функция между воздействием и откликом непараметрической линейной системы, если воздействие — белый шум?
![]()
Чему равна взаимная корреляционная функция между воздействием и откликом непараметрической линейной системы, если воздействие — белый шум?
![]()
Чему равна эквивалентная импульсная переходная функция последовательных линейных систем?
![]()
Чему равна эквивалентная импульсная переходная функция параллельных линейных систем?
![]()
Что такое линейный случайный процесс в узком смысле?
Что такое линейный случайный процесс в широком смысле?
Лет5
