
- •1) Этапы развития электротехники.
- •2) Преимущества электрической энергии перед другими видами энергии.
- •3) Основные элементы электрических цепей.
- •4) Параметры электрических цепей
- •5) Схемы электрических цепей.
- •6) Закон Ома.
- •7) Законы Кирхгофа.
- •8) Источники эдс и источники тока.
- •9) Последовательное, параллельное и смешанное соединение элементов.
- •10) Работа и мощность электрической цепи:
- •11) Баланс мощности ,мощность потерь и кпд
- •12) Режимы работы электрической цепи
- •15) Расчет сложных эл. Цепей с помощью законов Кирхгофа
- •16) Метод контурных токов
- •17) Метод узловых потенциалов
- •18) Метод двух узлов
- •19) Метод наложения тока
- •20) Метод эквивалентного генератора
- •21) Потенциальная диаграмма
- •22) Основные законы цепей переменного тока
- •24) Величины,характеризующие синусоидальную функцию времени
- •25) Виды представления синусоидальной функции
- •26) Законы Киргофа в комплексной форме.
- •27) Нагрузка в цепях переменного тока
- •28) Цепь переменного тока с активной нагрузкой.
- •29) Цепь переменного тока с индуктивной нагрузкой
- •30) Емкостное сопротивление
- •31) . Последовательное соединение активного сопротивления r, конденсатора с и индуктивности l
- •32) Параллельное соединение конденсатора и катушки, обладающей активным сопротивлением и индуктивностью
- •33) Цепь переменного тока со смешанным соединением элементов.
- •34. Мощность цепей переменного тока. Баланс мощности.
- •35. Резонанс напряжений.
- •36) Резонанс токов.
- •37. Получение трехфазной системы эдс.
- •38.) Соединение трехфазных приемников звездой
- •39). Соединение трехфазных приемников треугольником
- •40). Мощность в трехфазных цепях
- •Мощность трехфазной системы
- •41). Устройство и принцип действия трансформатора
- •42). Эдс, индуктируемые в обмотках трансформатора
- •43). Уравнения электрического состояния трансформатора
- •44.) Потери в трансформаторе
- •45) Режим холостого хода трансформатора.
- •46) Режим короткого замыкания трансформатора
- •47) Режим работы трансформатора под нагрузкой. Внешняя характеристика трансформатора
24) Величины,характеризующие синусоидальную функцию времени
В линейных цепях син-го тока и напряжения , ЭДС, и ток явл. син-ми фун-ми времени :
![]()
![]() где
u,e,i-мгновенные
значения напряжения ,ЭДС,тока,т.е.
значения этих величин в рассматриваемый
момент времини; (t+
где
u,e,i-мгновенные
значения напряжения ,ЭДС,тока,т.е.
значения этих величин в рассматриваемый
момент времини; (t+![]() ),(t+
),(t+![]() ),(t+
),(t+![]() )-аргумент
син-й функции, .-фазой или фазовым углом
.Как следует из рис.(шпора№23рис.1)каждая
син-я функция времени однозначно опред.
3-я параметрами :
)-аргумент
син-й функции, .-фазой или фазовым углом
.Как следует из рис.(шпора№23рис.1)каждая
син-я функция времени однозначно опред.
3-я параметрами :
Амплитудой Um, Em, Im(макс.значение син-й функции)
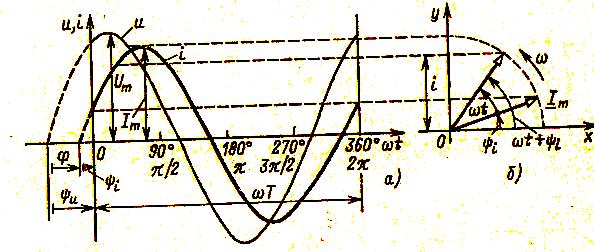
Угловой частотой w(скорость изменения аргумента син-й фун-и),гдеw-в рад/с;Начальной фазой
, , (значение аргумента син-й фун-и в момент начала отсчета времени, т.е. при t=0)в рад. или град.Кроме того ,для хар-ки син-х фун-й времени используют :
1)Период T=
2п/w-наименьший интервал
времени ,по истечении которого мгновенные
значения периодической величены
повторяются .2)Частота f=1/Т,т.е.
число периодов в секунду (Гц).3)Сдвиг фаз
м/д напряжением и током
![]() -алгебраич-я
вел. опред. как разность фаз ,напряж. и
тока .4)Действующее значение
U,E,I-среднеквадратичное
значение переменной величены за период.
-алгебраич-я
вел. опред. как разность фаз ,напряж. и
тока .4)Действующее значение
U,E,I-среднеквадратичное
значение переменной величены за период.
![]() 5)средние
значения Iср,Uср,Eср.Средние
значение син-й фун-ии за период =0
(одинаковые площади положительной и
отрицательной полуволн синусоиды)
5)средние
значения Iср,Uср,Eср.Средние
значение син-й фун-ии за период =0
(одинаковые площади положительной и
отрицательной полуволн синусоиды)
25) Виды представления синусоидальной функции
Способы представления синусоидальной величины:
1.Аналитическое: i(t)= Imsin(t+).
2.
Изображение синусоидальной величины
при помощи векторов. Оно позволяет
наглядно показать количественные и
Фазовые соотношения в цепях синус-го
тока. Длина вектора должна быть равна
амплитуде тока, а угол наклона к оси
абсцисс- начальной фазе тока. Его проекция
на ось ординат =мгновенному значению
тока в момент времени t=0.
Будем вращать вектор Im
с постоянной скоростью w
вокруг начала координат против направления
часовой стрелки. Проекция вращ-ся вектора
на ось ординат I=Imsin(wt+![]() )
и представляет собой мгновенное значение
тока – синус-ю функцию. Изобр.
синусоид.
изм-ся
вел.
комплекс. числами.д
)
и представляет собой мгновенное значение
тока – синус-ю функцию. Изобр.
синусоид.
изм-ся
вел.
комплекс. числами.д

Imsin(t+).
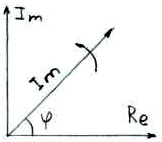
3) В виде комплексных чисел.

Комплексное число – сумма действительной и мнимой части.
![]()
Алгебраическая форма записи комплексного числа:
![]() ,
,
![]() ,
,
![]() .
.
![]() -
тригонометрическая форма записи
комплексного числа.
-
тригонометрическая форма записи
комплексного числа.
А- модуль комплексного числа.
![]() .
.
- аргумент комплексного числа.
![]() ,
,
![]() .
.
![]() -
ф-ла Эйлера, показательная форма записи
комплексного числа.
-
ф-ла Эйлера, показательная форма записи
комплексного числа.
![]() -
оператор поворота показывает что вектор
повернут относительно вещественной
оси в (+) направлении на угол
.
-
оператор поворота показывает что вектор
повернут относительно вещественной
оси в (+) направлении на угол
.
26) Законы Киргофа в комплексной форме.
1-закон Киргофа: алгебраическая сумма комплексных токов в узле электр. цепи равна нулю.
![]()
2-закон Киргофа: алгебраическая сумма комплексных напряжений в контуре равна алгебраической сумме комплексных ЭДС в том же контуре.
![]()
27) Нагрузка в цепях переменного тока
Активная- нагрузка на которой электрическая энергия превращается в другой вид энергии(активное сопротивление).
Реактивная – нагрузка на которой происходит периодический обмен энергии(емкостной, индуктивный эл-т).
