Пример.

Пусть числовая последовательность имеет вид . Тогда соответствующее Z‑преобразование будет иметь:

.

В табл. 1 приведен перечень наиболее важных и часто употребляемых Z‑преобразований некоторых числовых последовательностей.

Таблица 1

Z‑преобразования некоторых числовых последовательностей.

(Символ Кронекера)

Выражение (1.8) используется при нахождении Z‑преобразования функции. Однако неудобство этого выражения состоит в том, что оно является бесконечным рядом, а не эквивалентной функцией в комплексной форме. Альтернативное выражение для Z‑преобразования можно получить, если непрерывный сигнал задан преобразованием Лапласа. Тогда:

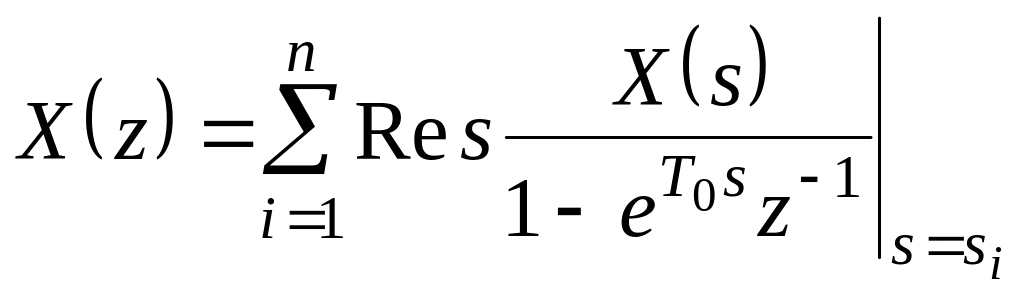; (1.9)

где  – полюсы функции .

Пример. Найдём z‑преобразование единичной ступенчатой функции.

1-й способ.

1. Единичная ступенчатая функция квантуется идеальным квантователем, при этом его выходным сигналом является последовательность единичных импульсов:

;

2. Преобразуя по Лапласу, найдём

;

3. Умножим обе части последнего равенства на 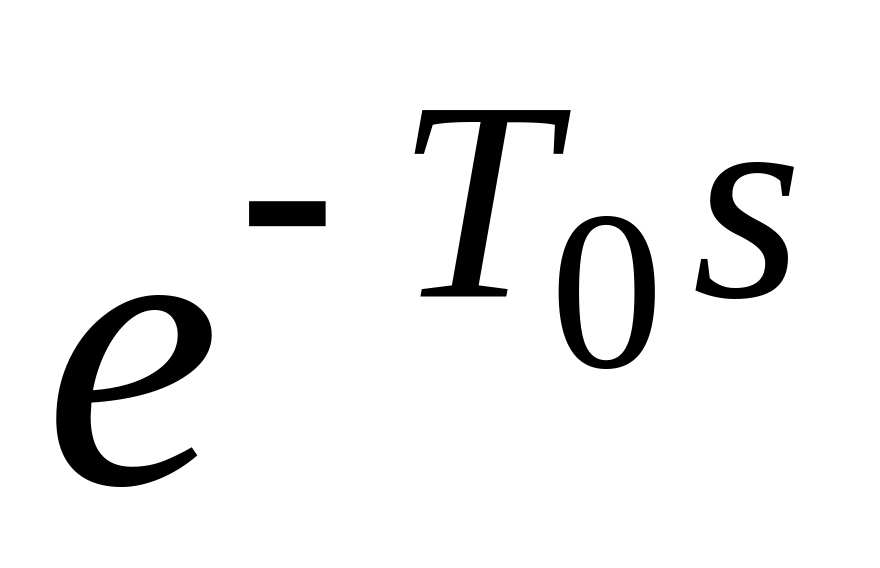и вычтем результат из последнего равенства, тогда

для .

4. .

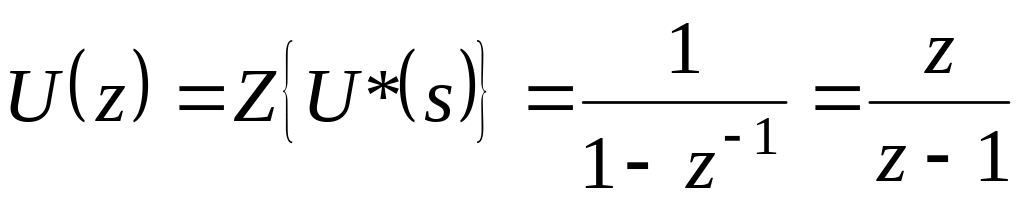Тот же результат можно получить, применяя формулу (1.6). Действительно, преобразование Лапласа имеет простой полюс .

Следовательно,

Свойства Z-преобразования.

Рассмотрим основные свойства Z‑преобразования, используемые в дальнейшем для анализа систем цифрового управления.

1. Линейность – выполняется принцип суперпозиции:

.

2. Предельные теоремы:

а) О начальном значении решетчатой функции:

.

б) О конечном значении:

.

Теоремы справедливы, если все пределы существуют.

3. Теорема о смещении во временной области:

.

При целых значениях имеем:

. (1.10)

Если выполняется условие при , то можно также определить Z‑преобразование числовой последовательности , опережающей на один такт указанную последовательность :

.

Переходя к обобщённому представлению:

. (1.11)

Формулы (1.10) и (1.11) широко используются при решении разностных уравнений и при нахождении Z‑преобразования уравнений состояния.

Обратное Z-преобразование - это восстановление решетчатой функции по её Z‑изображению. Обратное Z‑преобразование обозначается так:

.

Следует отметить, что обратное Z-преобразование в отличие преобразования Лапласа является неоднозначным в том смысле, что совпадает с только в моменты квантования.

В общем случае обратное Z-преобразование может быть определено одним из трёх методов:

1. Разложение на элементарные дроби. Используется, если Z‑изображение – дробно‑рациональная функция. После разложения для каждой элементарной дроби находят по таблице соответствующую решетчатую функцию.

Приведём таблицу некоторых наиболее важных и часто употребляемых Z‑преобразований.

Таблица 2

Некоторые функции времени и их преобразования Лапласа и z‑преобразования

2. Применение общей интегральной формулы: 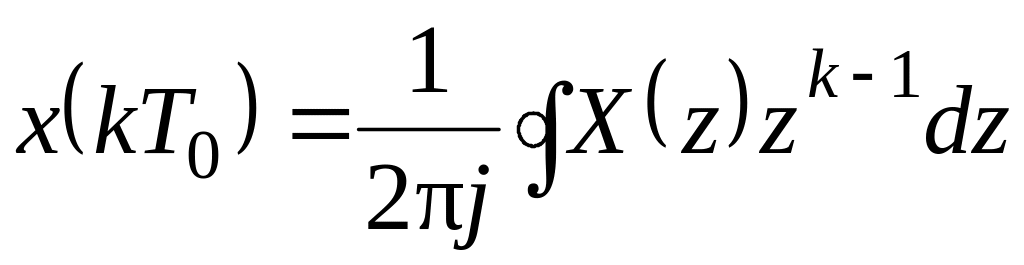. Интегрирование ведётся по контуру, включающему все особые точки подынтегральной функции.

3. Разложение в ряд Лорана – степенной ряд по отрицательным степеням : .

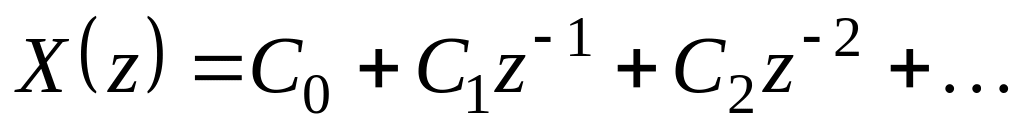Сравнение с формулой Z-преобразования

;

дает:

; ; .

Для дробно-рациональной функции ряд Лорана получается простым делением числителя на знаменатель.

Пример 1.

Дано Z-преобразование . Требуется найти обратное преобразование, т.е. .

1. Применим метод разложения на простейшие дроби 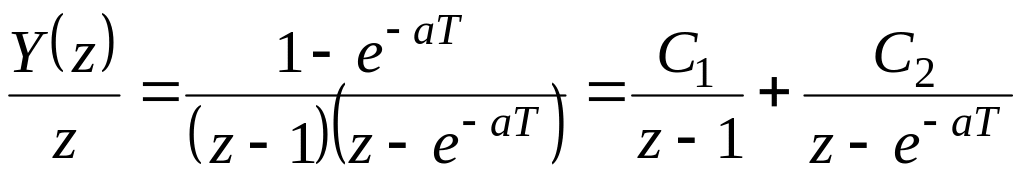, откуда .

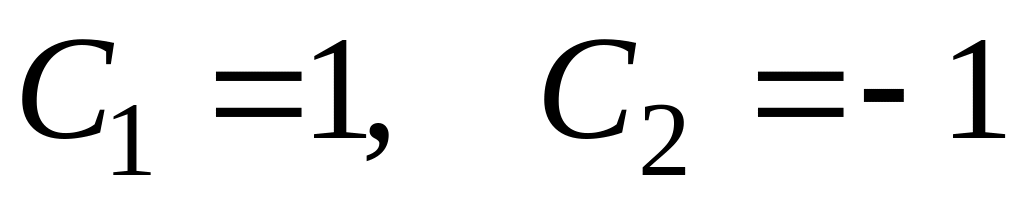Следовательно, .

Из табл. 2 Z-преобразований найдём .

Следовательно, дискретная временная функция может быть записана в виде:

.

2. Применим метод разложения в степенной ряд.

Последовательное деление числителя на знаменатель даёт: , откуда согласно табл. 1:

, где .

Используя формулу обращения, получим:

;

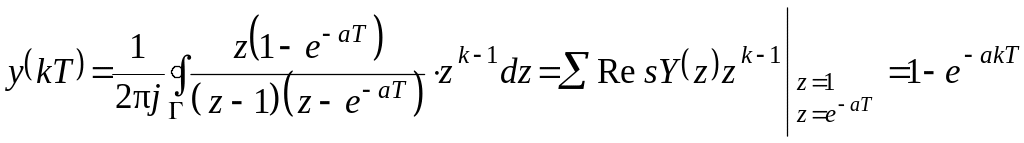где  – окружность, включающая в полюсы в точках, ,

Пример 2.

Пусть требуется найти решение уравнения в конечных разностях типа: при , , .

Осуществим Z-преобразование функции и обеих частей уравнения:

;

или

;

откуда

;

Представим

;

Домножая на , получим:

.

Используя табл. 1 Z-преобразования, найдём:

, .