
- •1. Алгоритм и его свойства (рассмотреть алгоритм умножения).
- •2. Языки программирования.
- •3. Разветвляющиеся алгоритмы. Алгоритм вычисления арксинуса - агсsin х.
- •4. Программа вычисления арксинуса - Агcsin.
- •5. Программа расчета машинного "эпсилона" - Ерsilon.
- •6. Циклические алгоритмы. Программа вычисления конечного произведения (степени числа а).
- •7. Циклические алгоритмы. Алгоритм вычисления бесконечного произведения.
- •8. Циклические алгоритмы. Программа вычисления бесконечного произведения.
- •9. Программа вычисления гипотенуз с использованием функции Роwer.
- •10. Процедура РrintLine и ее использование в программах.
- •11. Процедура МахМin и ее вызов с различными параметрами.
- •12. Процедура сортировки одномерного массива.
- •13. Задача поиска корней уравнения. Метод половинного деления.
- •14. Алгоритм метода половинного деления.
- •15. Метод простой итерации для поиска корней. Геометрическая интерпретация.
- •16. Приведение уравнения к виду, пригодному для применения метода итераций.
- •17. Общая оценка погрешности приближения к корню.
- •23. Оценка погрешности приближения в методе простой итерации.
- •24. Метод Ньютона и оценка погрешности приближения
- •25. Модификации метода Ньютона и оценка погрешности приближения.
- •26. Метoд хорд и оценка погрешности приближения.
- •1.6. Метод хорд
- •27. Понятие нормы. Нормы векторов в конечномерном пространстве
- •28. Нормы матриц. Согласованность и подчиненность норм.
- •29. Обусловленность систем уравнений. Коэффициент обусловленности.
- •Таким образом
- •30. Свойства коэффициента обусловленности
- •31. Решение систем линейных алгебраических уравнений. Метод Гаусса.
- •32. Алгоритм метода Гаусса.
- •33. Метод Гаусса с выбором главного элемента
- •34. Решение систем линейных алгебраических уравнений методом прогонки.
- •35. Алгоритм метода прогонки.
- •36, Метод простой итерации для решения систем линейных алгебраических уравнений.
- •37. Сходимость последовательности векторов и матричной прогрессии.
- •38. Сходимость метода простой итерации для решения систем линейных уравнений
- •39. Оценки погрешности метода простой итерации для решения систем уравнений.
- •40. Метод Зейделя для решения систем линейных алгебраических уравнений.
- •41. Алгоритм метода Зейделя.
- •Xnew←t*pi
- •XI← xnew
- •42. Метод последовательной верхней релаксации.
- •43. Постановка и решение задачи интерполирования функции.
- •44. Алгебраическое интерполирование.
- •45. Интерполяционный полином в форме Лагранжа.
28. Нормы матриц. Согласованность и подчиненность норм.
Введём понятие нормы матрицы. Нормой матрицы назовем поставленное в соответствие этой матрице вещественное число ||A|| такое, что которое как вещественное число ставится в соответствие каждой матрице из n-мерного пространства и удовлетворяет 4 аксиомам:
||A||0 и ||A||=0, только если A – нулевая матрица;
||αA||=|α|·||A||, где R;
||A+B||||A||+||B||;
||A·B||||A||·||B||. (свойство мультипликативности)
Норма матрицы, как и норма вектора, может быть введена различными способами. Матрицу A, например, можно рассматривать как n2-мерный вектор. Тогда естественным обобщением сферической (евкдидовой) нормы вектора будет являться следующая:
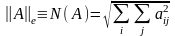 .
.
Эта норма называется евклидовой нормой матрицы.
Пусть выбрана некоторая норма вектора. Если для любой квадратной матрицы A и любого вектора x, размерность которого равна порядку матрицы, выполняется неравенство
||Ax||||A||·||x||,
то говорят, что норма матрицы A согласована с нормой вектора. Заметим, что слева в последнем условии стоит норма вектора (Ax – вектор).
С заданной векторной нормой согласованы различные матричные нормы. Выберем среди них наименьшую. Таковой будет
 .
.
Эту матричную норму называют подчиненной заданной векторной норме. Существование максимума в этом выражении следует из непрерывности нормы, ибо всегда существует вектор x такой, что ||x||=1 и ||Ax||=||A||.
Нетрудно показать, что норма N(A) не подчинена ни одной векторной норме. Нормы матрицы, подчиненные ранее введенным векторным нормам, выражаются следующим образом:
||A||=
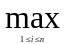
 |aij|
(норма-максимум)
|aij|
(норма-максимум)||A||1=

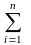 |aij|
(норма-сумма)
|aij|
(норма-сумма)
||A||2=
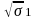 ,
(спектральная норма)
,
(спектральная норма)
где
1
является
наибольшим собственным значением
симметричной матрицы AA,
являющейся произведением транспонированной
и исходной матриц. Поскольку матрица
AA
симметричная, то все ее собственные
значения вещественны и положительны.
Напомним, что число
называется собственным значением, а
ненулевой вектор x
– собственным вектором матрицы A,
если они связаны между собой соотношением
Ax=x.
Если же матрица A
сама является симметричной, A
= A,
то AA
= A2
и тогда 1
=
 ,
где
,
где
 - наибольшее по модулю собственное
значение матрицы A.
Следовательно, в этом случае мы имеем
- наибольшее по модулю собственное
значение матрицы A.
Следовательно, в этом случае мы имеем
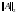 =
=
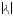 .
.
Заметим, что собственные числа матрицы не превышают любой из ее согласованных норм. Действительно, нормируя определяющее собственные числа соотношение, получим
||λx||=||Ax||, |λ|·||x||=||Ax||||A||·||x||, |λ|||A||.
Вычисление спектральной нормы – трудоемкая задача. Однако, поскольку справедливо неравенство ||A||2||A||e, где евклидова норма вычисляется просто, в оценках вместо спектральной нормы можно использовать евклидову норму матрицы.
