16. Полярная система координат. Деление отрезка в данном отношении.

Полярная система координат задается точкой О, называемой полисом, лучом О_р, называемым полярной осью, и единичным вектором 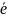того же направления, что и луч О_р.

М(r;

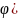
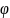
r

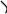
О

Числа r и называются полярными координатами точки М, пишут М(r; ), при этом r называют полярным радиусом, – полярным углом.

Прямоугольные координаты точки М выражаются через полярные координаты точки следующим образом:

Полярные координаты точки М выражаются через её декартовы координаты:

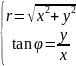
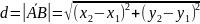
Деление отрезка в данном соотношении.

Требуется разделить отрезок АВ, соединяющий точки А(х₁;у₁) и В(х₂;у₂) в заданном отношении >0, т.е. найти координаты точки М(х;у) отрезка АВ такой, что

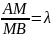
Формулы деления отрезка в данном отношении:

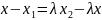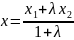
, т.е.

, т.е.

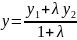
17. Преобразование системы координат. Формулы перехода от одной системы координат к другой.

Переход от одной системы координат к какую-либо другую называется преобразованием системы координат.

1. Параллельный перенос осей координат.

Пусть на плоскости задана прямоугольная система координат О_ху. Под параллельным переносом осей координат понимают переход от системы координат О_ху к новой системе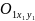 , при котором меняется положение начала координат, а направление осей и масштаб остаются неизменными. Приведенные ниже формулы позволяют находить старые координаты х и у по известным новым х^l и у^l и наоборот.

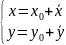
2) Поворот осей координат.

Под поворотом осей координат понимают такое преобразование координат, при котором обе оси поворачиваются на один и тот же угол, а начало координат и маштаб остаются неизменными.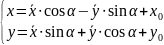

18. Общее уравнение прямой на плоскости. Уравнение прямой, проходящей через её точки.

Рассмотрим уравнение первой степени относительно х и у в общем виде А_х+В_у+С=0(1), где А,В,С – произвольные числа, причем А и В не равны нулю одновременно. Покажем, что вышеприведенное уравнение есть уравнение прямой линии. Возможны два случая.

Если В=0, то уравнение (1) имеет вид А_х+С=0, причем А≠0, т.е. 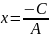. Это и есть уравнение прямой, параллельной оси О_у и проходящей через точку .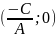

Если В≠0, то из уравнения (1) получаем 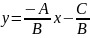. Это есть уравнение прямой с угловым коэффициентом .

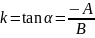Итак, уравнение (1) есть уравение прямой линии, оно назвается общим уравением прямой.

Частные случаи:

1. Если А=0, то уравнение приводится к виду 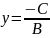. Это и есть уравнение прямой, параллельной оси О_х.

2. Если В=0, то прямая параллельна оси О_у.

3. Если С=0, то получаем А_х+В_у=0. Уравнению удовлетворяют координаты точки О(0;0), прямая проходит через начало координат.

Уравнение прямой, проходящей через данную точку в данном направлении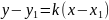 (так же называется уравнениями пучка прямых с центром в точке М(х₀;у₀). Определить нельзя лишь прямую, параллельную оси О_у)

Уравнение прямой, проходящей через две точки.

Пусть прямая проходит через точки М₁(х₁;у₁) и М₂(х₂;у₂). Уравнение прямой, проходящей через точку М₁, имеет вид: у-y₁=k(x-x₁), где k неизвестный пока коэффициент.

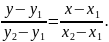
Уравнение прямой в отрезках.

Это уравнение называется уравнением прямой в отрезках, так как числа указывают, какие отрезки отсекает прямая на осях координат.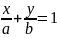

19.Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.

Возьмем на прямой произвольную точку М(х;у) и рассмотрим вектор М₀М=(х-х₀;у-у₀). Поскольку векторы n и векторы М₀М перпендикулярны, то их скалярное произведение равно нулю.

Вектор перпендикулярный прямой, называется нормальным вектором этой прямой.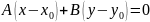

20. Угол между двумя прямыми на плоскости.

Пусть прямые l1 и l2 заданы уравнениями с угловыми коэффициентами y=k₁x+b₁ и y=k₂x+b₂.

Требуется найти угол , на которой надо повернуть в положительном направлении прямую L₁ вокруг точки их пересечения до совпадения с прямой L₂

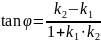
Условие параллельности двух является равенство их угловых коэффициентов k₁=k₂

21. Расстояние от точки до прямой.

Расстояние d от точки М₀ до прямой L равно модулю проэкции вектора М₁М₀, где М₁(х₁;у₂) ­ произвольная точка прямой L, на направление нормального вектора n= (А;В). Так как точка М₁= принадлежит прямой L, то Ах₁+Ву₁+С=0, т.е. С=-Ах₁-Ву₁.

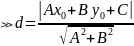
22. Каноническое уравнение окружности. Общее уравнение окружности.

Окружность – это множество всех точек М плоскости, удовлетворяющих М₀М=R. Пусть точка М₀М=R. 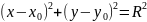- каноническое уравнение окружности. 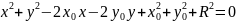; 1) Коэффициенты при х² и у² равны между собой; 2) отсутствует член, содержащий произведение ху текущих координат.

Общее уравнение окружности:

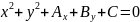
23. Эллипс. Каноническое уравнение эллипса.

Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Каноническое уравнение эллипса. .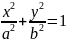

Эллипс – кривая второго порядка.

24. Экцентриситет эллипса. Выражение фокальных радиусов. Эллипс через его экцентриситет и большую полуось.

Экцентриситет эллипса – отношение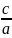 половины расстояния между фокусами к большой полуоси эллипса.

Чем меньше эксцентриситет эллипса, тем эллипс будет менее сплющенным; если положить 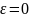, то эллипс превращается в окружность.

Пусть точка М(х;у) – произвольная точка эллипса с фокусами F₁ и F₂. Длины отрезков F₁M=r₁, и F₂M=r₂, называются фокальными радиусами точки М.

r₁+r₂=2a; r₁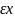=a+ ; r₂=a- .