10. Линейная зависимость и независимость векторов. Базис.

Error 404 not found 

11. Скалярное произведение векторов и его свойства.

Скалярным произведением двух ненулевых векторов 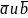называется число, равное произведению длин этих векторов на косинус угла между ними

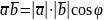
Скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.

Свойства скалярного произведения.

1. Скалярное произведение обладает переместительным свойством:

2. Скалярное произведение обладает сочетательным свойством относительно скалярного множителя:

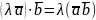
3. Скалярное произведение обладает распределительным свойством: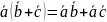

4. Скалярный квадрат вектора равен квадрату его длины: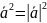

5. Если векторы (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т.е. если 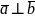, то

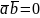
12. Векторное произведение векторов и его свойства.

Векторным произведением вектора 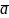и называется вектор 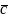, который: 1)перпендикулярен векторам

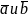
2) имеет длину, численно равную площади параллелограмма, построенного на векторах и как на сторонах

3) векторы , и образуют правую тройку.

Свойства векторного произведения.

1. При перестановке сомножителей векторное произведение меняет знак.

2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя.

3. Два ненулевых вектора и коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору.

4. Векторное произведение обладает распределительным свойством.

13. Векторное произведение векторов в координатах.

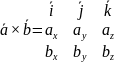
Чотипавсё?

14. Смешанное произведение векторов и его свойства.

Рассмотрим произведение векторов a b и с, составленное следующим образом . Здесь первые два вектора перемножаеются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторно-скалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.

Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком “плюс”, если эти векторы образуют правую тройку, и со знаком “минус”, если они образуют левую тройку.

Свойства смешанного произведения.

1. Смешанное произведение не меняется при циклической перестановке его сомножителей

2. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения

3. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей

4. Смешанное произведение ненулевых векторов , и равно нулю тогда и только тогда, когда они компланарны.

15. Выражение смешанного произведения через координаты. Некоторые приложения смешанного произведения.

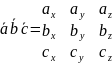
Смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.

Определение взаимной ориентации векторов в пространстве.

Определение взаимной ориентации векторов , и основано на следующих соображениях. Если >0, то 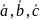– правая тройка; если <0, то – левая тройка.

Установление компланарности векторов.

Векторы 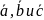компланарны тогда и только тогда, когда их смешанное произведение равно 0.

Определение объемов параллелепипеда и треугольной пирамиды.

Параллелепипед:

.

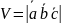Тетраэдр:

.
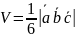