8. Решение однородных систем линейных уравнений.

Для того, что бы система однородных уравнений имела ненулевые решения, необходимо и достаточно, что бы ранг r её основной матрицы был меньше числа n неизвестных, т.е. r<n.

Необходимость.

Так как ранг не может превосходить размера матрицы, то, очевидно, r≤n. Пусть r=n. Тогда один из миноров размера n x n отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение: х_j= ∆_j/∆=0 , ∆_j=0 , ∆≠0. Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то r<n.

Достаточность.

Пусть r<n. Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т.е. имеет и ненулевые решения.

Для того, чтобы однородная система т линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, что бы её определитель ∆ был равен нулю, т.е. ∆=0.

Если система имеет ненулевые решения, то ∆=0. Ибо при ∆≠0 система имеет только единственное, нулевое решение. Если же ∆=0, то ранг r основной матрицы системы меньше числа неизвестных, т.е. r<n. И, значит, система имеет бесконечное множество (ненулевых) решений.

9. Векторы и действия над ними.

Вектор – это направленный прямолинейный отрезок, т.е. отрезок, имеющий определенную длину и определенное направление. Если А – начало вектора, а В – его конец, то вектор обозначается символом­ или 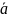. Вектор 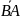( у него начало в точке В, а конец а точке А) называется противоположным вектору , Вектор, противоположный вектору , обозначается - .

Длиной или модулем вектора называется длина отрезка и обозн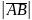ачается . Вектор, блина которого равна нулю, называется нулевым вектором и обозначается .

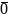Вектор, длина которого равна единице называется единичным вектором и обозначается через 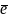. Единичный вектор, направление котрого совпадает с направлением вектора называется ортом вектора и обозначается ⁰.

Векторы и 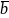называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают как .

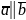Коллинеарные векторы могут быть направлены одинаково, или противоположно.

Нулевой вектор считается коллинеарным любому вектору.

Два вектора и называются равными если они коллинеарны, одинаково направлены и имеют одинаковые длины.

Линейные операции над векторами.

Сложение. Правило треугольников.

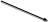
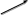
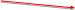
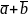
Сложение. Правило параллелограмма.

Сложение трех векторов.

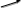
Вычитание векторов(см. зелёная стрелка)

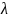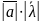Произведением вектора на скаляр(число) называется вектор который имеет длину , коллинеарен вектору , имеет направление вектора , если >0 и противоположное направление, если <0.

Проэкция вектора на ось.

Проэкцией точки M на ось l называется основание M­­­­­­­₁­­ перпендикуляра ММ₁, опущенного из точки на ось.

Точка М₁ есть точка пересечения оси l с плоскостью, проходящей через точку М перпендикулярно оси.

l

Проекция вектора на ось l равна произведению вектора на косинус угла между вектором и осью, т.е. пр_l = .

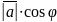Проекция вектора на ось положительна(отрицательна), если вектор образует с осью острый(тупой) угол, и равна нулю, если этот угол – прямой.

Проэкции равных векторов на одну и ту же ось равны между собой.

Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось.

При умножении на число его проекция на ось также умножается на это число.