36) Общий прядок определения главных центральных моментов инерции. Пример:

1. Если фигура имеет две оси симметрии, то эти оси и будут ГЦО.

2. Для правельных фигур ( у которых больше 2- х оссей) все оси будут главными

3. Проводим вспомогательные оси(Х’ O’ Y’)

4. Разбиваем данное сечение на простые фигуры и показываем их собственные ЦО.

5. Находим положение ГЦО по формуле(21)

6. Вычисляем значения ГЦМ по формуле (23)

• Imax + Imin = Ix + Iy

• Imax >Ix>Iy>Iminесли Ix>Iy

• Iuv = Ix-Iy/2 sin2a + Ixycos2a +0

Формула 21:Tg2a = - 2Ixy/Ix - Iy

Формула23: Imax, Imin = *

37) Изгиб. Классификация видов изгиба. Прямой и чистый изгиб. Картина деформирования балки. Нейтральный слой и ось. Основные допущения.

Изгиб – деформирование при котором в поперечном сечении возникает изгибающий момент Мх. Брус, который работает на изгиб-балка

Виды изгиба:

Чистый изгиб имеет место, если в сечении возникает только изгибающий момент

Поперечный изгиб- если одновременно с моментом возникает поперечная сила

Плоский - все нагрузки лежат в одной плоскости

Пространственный - если все нагрузки лежат в разных продольных плоскостях

Прямой - если силовая плоскость совпадает с одной из главных осей инерции

Косой - если силовая плоскость не совпадает ни с одной из главных осей

В результате деформирования на участке чистого изгиба можно видеть:

- продольные волокна искривляются по дуге окружности: одни- укорачиваются, другие-удлиняются; между ними есть слой волокон, которые не меняют своей длины- нейтральный слой (н.с.), линию его пересечения с плоскостью поперечного сечения называют нейтральной осью (н.о.)

-расстояние между продольными волокнами не меняется

-поперечные сечения, оставаясь прямыми, поворачиваются на некоторый угол

Допущения:

1.Оненадавливании продольных волокон друг на друга, т.е. каждое волокно находиться в состоянии простого растяжения или сжатия, что сопровождается возникновением нормальных напряжений Ϭ

2.О справедливости гипотезы Бернули, т.е. сечения балки, плоские и нормальные к оси до деформации, остаются плоскими и нормальными к ее оси после деформации

38) вывод формулы нормальных напряжений при изгибе. Закон Гука при изгибе. Анализ формулы напряжений(эпюры напряжений). Осевой момент сопротивления: формула и вывод формул для простых фигур

При чистом изгибе в сечении балки возникает только изгибающий момент Мх, остальные внутренние усилия равны нулю (N=0,My=0 и т.д).следовательно, на площадке dA будет действовать только напряжение Ϭ

Статическая сторона задачи

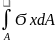N= =0 ;My= =0 ;Mx=

Геометрическая сторона(гипотеза плоских сечений)

cd=ab=dz;dz=ρdθ

bb’=ydθ

ε= (ρ-радиус кривизны нейтрального слоя),у-растояние от волокна до нейтральной слоя

ε= , т.е деформация волокна пропорциональна его расстоянию до нейтрального слоя

закон Гука:

ε=

Ϭ=Еу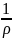 эту формулу свяжем с внутренними усилиями.

N=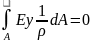

N=

Нейтральная ось проходит через центр тяжести

Ϭ=

Из анализа формулы следует:

1.Напряжение Ϭ изменяются по высоте сечения линейно

2. По ширине сечения Ϭ распределены равномерно( не зависят от координаты х)

3. Напряжение Ϭ=0 при у=0,т.е. на нейтральной оси

4. Напряжения максимальны там, где у_max, т.е. в точкахнаиболее удаленных от нейтральной оси; будем называть эти точки опасными

Ϭ_max=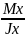 y_maxили Ϭ_max=

Wx= -осевой момент сопротивления сечения, характеризует сопротивляемость балки изгибу, зависит от формы и размеров сечения

Прямоугольник Wx= аналогично Wy=

Круг Wx=Wy=

Кольцо

Jx= ,

Wx=

39) Расчеты на прочность при чистом изгибе для различных материалов. Рациональное сечение балки и рациональное расположение сечения. Примеры. Условия прочности по предельным состояниям

Балки из материалов одинаково сопротивляющихся растяжению и сжатию (сталь, древесина), проектируются симметричными относительно оси х.

Условие прочности по допускаемым напряжениям Ϭ_max= [Ϭ]

по предельным состояниям

Ϭ_расч.=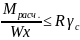 ,М_расч.-наибольший по абсолютному значению изгибающий момент от расчетных нагрузок; R-расчетное сопротивление материала балки растяжению(сжатию) при изгибе; [Ϭ]-допускаемое напряжение

Для получения рационального сечения балки нужно большую часть располагать как можно дальше от оси.

Нагрузку прикладывают к плоскости наибольшей жесткости,которая совпадает с осью

Сплошное сечение менее рационально, чем полое, при одинаковых материалах

Для балок из хрупких материалов, различно сопротивляющихся растяжению и сжатию, следует применять сечения несимметричные относительно нейтральной оси ( тавровое, несимметричное двутавровое, П-образное). При этом целесообразно располагать сечение так, чтобы большая его часть сечения находилась в растянутой зоне

Ϭ_pmax= [Ϭ_p] ;

Ϭ_tрасч.= [R_tγ_c]и

Ϭ_{c max}= [Ϭ_c ;

Ϭ_cрасч.= [R_cγ_c], где -расстояние от нейтральной оси до наиболее отдаленных точек растянутой и сжатой зон; R_tи R_с-расчетные сопротивления материала на растяжение и сжатие;[Ϭ_p] и [Ϭ_с]–допускаемые напряжения при

растяжение и сжатие

40) Потенциальная энергия деформации при чистом изгибе

Работа статически приложенной силы в пределах упругих деформаций численно равна потенциальной энергии деформации.

Потенциальной энергией деформации называется энергия, которая накапливается в теле при его деформировании.

Работа изгибающего момента Мх, при деформировании элемента dz вычисляется как половина произведения момента на соответствующий угол поворота dθ.

dW = = dU = ½ Mxdθ (7.27)

Отрезок на нейтральной оси элементаdz = ρdθ, отсюда dθ = 1/ρdz

По формуле: 1/ρ = Mx/EIxТогдаdθ = Mx/EIx *dz. Подставляем это выражение в (7.27), имеем :dU=M²xdz/2EIx

Суммируя значения dU по всей длине балки, получим формулу потенциальной энергии при чистомизгтбе: U =

При вычислении U следует учитывать, что закон изменения Мх для отдельных участков различен.

41. Поперечный изгиб и его отличие от чистого. Закон парности касательных напряжений.

В поперечном сечении балки одновременно с изгибающим моментом возникает поперечная сила

В поперечном сечении наряду с нормальными напряжениями возникают касательные напряжения τ

В продольных сечениях на основании закона парности появляются касательные напряжения ,которые вызывают сдвиги отдельных волокон.

Вследствие сдвигов волокон плоские сечения до деформации искривляются, принимая форму вытянутой буквы S, особенно в средней части балки, т.е. нарушается гипотеза плоских сечений.

Закон о парности: на взаимно перпендикулярных площадках касательные напряжения равны по величине и противоположны по знаку.

42. Вывод формулы касательных напряжений при изгибе (формула Журавского)

Поскольку

43. Анализ формулы Журавского: для прямоугольного и двутаврового сечения. Сопоставление наибольших нормальных и касательных напряжений при изгибе.

Прямоугольное сечение

Двутавровое сечение

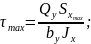
Сопоставление нормального и касательного напряжения

Касательное напряжение

Касательные напряжения

, т.е. нормальные напряжения значительно больше касательных

В прокатной и сварной двутавровой балке, имеющей сравнительно большую высоту, касательные напряжения могут быть значительны при условии, что длина балки невелика и загружена она большими сосредоточенными силами, приложенными близко к опорам.

44. Расчеты на прочность при поперечном изгибе. Условия прочности. Расчет сплошных и тонкостенных сечений, деревянных и клееных балок, двутавровых балок.

Условия прочности по касательным напряжениям

Метод допускаемых напряжений:

Метод предельных состояний:

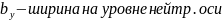
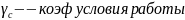
Три вида расчета:

Проверка прочности

Подбор ширины прямоугольного сечения балки (проектный расчет)

Предельная поперечная сила (несущая способность) опред:

Условия прочности по нормальным напряжениям

Для балок сплошного сечения основной расчет по нормальным напряжениям, расчет по касательным носит вспомогательный характер.

Для тонкостенных профилей, деревянных и клееных балок обязательно делается проверка по касательным напр. Если условие не выполняется, то подбирают другое сечение.

45. Перемещение при изгибе (линейные и угловые). Точное и приближенное уравнение упругой линии балки. Определение перемещения методом непосредственного интегрирования. Пример.

Линейные перемещения-прогибы у - направлены перпендикулярно продольной оси z балки. Наибольший прогиб - стрела прогиба f.

Угол между новым и старым положением сечения - угол поворота

Точное уравнение упругой линии балки:

Приближенное уравнение упругой линии балки:

- уравнение углов поворота

- уравнение прогибов

Метод Непосредственного интегрирования

Разбивают балку на участки и для каждого записывают выражение изгибающего момента Mz

Для каждого участка составляют диф. уравнение, подставляя Mz

Для каждого участка диф. ур-е дважды интегрируют и получают общие выражения для угла поворота и прогиба у

Из условий на опорах балки и на границах участков определяют постоянные интегрирования C и D и подставляют в уравнения

Определяют и у в нужном сечении, подставляя значения z

Пример. Определить наибольший угол поворота и стрелу прогиба.

При z=0 угол поворота

При z=0 прогиб

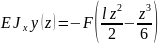
Полагая что z=l

Знак «минус» указывает на то, что поворот по часовой стрелке и что конец опускается вниз.

46. Метод начальных параметров. Вывод универсального уравнения при изгибе. Начальные параметры. Порядок (алгоритм) вычисления перемещений методом начальных параметров. Пример. Условие жесткости при изгибе.

Выбираем единое начало координат на левом конце балки

Если распределенная нагрузка не доходит до правого конца, продлеваем ее и показываем компенсирующую

,если на балку действует момент, где а - абсцисса до точки приложения силы

Интегрирование вести без раскрытия скобок

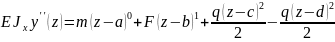
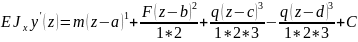
Начало координат совпадает с заделкой. Начальные параметры (рис)

Начало координат совпадает с шарнирной опорой

Начало координат находится на свободном конце

Находим из граничных условий

Порядок расчета:

Определяем опорные реакции и проставляем на расчетной схеме

Выбираем единое начало координат на левом конце балки и выявляем равны 0 начальные параметры или нет

Если нагрузка q не доходит до правого конца ее продлевают и показывают компенсирующую

Записываем универсальное уравнение прогиба обычно для последнего участка, учитывая силы расположенные левее рассматриваемого сечения, слагаемые имеют знак изгибающего момента

Дифференцируем уравнение и получаем формулу угла поворота

Если начальные параметры не равны 0 то их определяем из граничных условий

Подставляем в уравнения соответствующие значения z, определяем прогиб и угол поворота

Условие жесткости: наибольший прогиб не должен превышать предельно допустимого, устанавливаемого СНиПом.

;

47. Чистый сдвиг. Анализ напряженного состояния; закон Гука. Упругие постоянные материала и связь между ними. Потенциальная энергия.

Сдвиг – нагружение, когда в поперечном сечении возникает только поперечная сила Q.

Чистый сдвиг - явление, при котором на грани выделенного элемента действуют только касательные напряжения.

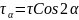
(рис)

Закон Гука

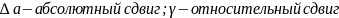
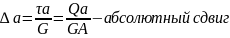
E- модуль продольной упругости

G – модуль сдвига

Потенциальная энергия

Удельная потенциальная энергия - численно равно площади треугольника на диаграмме сдвига

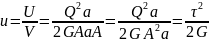
48. Понятие о срезе и смятии. Условия прочности. Расчет заклепочных соединений на прочность.

Срез- вид нагружения при котором в поперечном сечении возникает только поперечная сила Q.

Деформация среза сопровождается смятие, т.е. пластичные деформации, возникшие по поверхности контакта.

Расчет заклепочных соединений

Срез заклепок

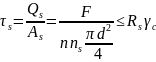
Смятие заклепок

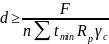
Чтобы прочность заклепки на срез и на смятие из 2-ч диаметров выбираем наибольший

Разрыв листа

Срез листа (выкалывание)

Чтобы срез не происходил расстояние не менее 2d. Подобно заклепкам работают болты и болтовые соединения. В высокопрочных соединениях болты не работают не на срез не на смятие, т.к. они закреплены с помощью специальных динамич. Ключей или машин.

49. Соединения на врубках. Условия прочности на скалывание и смятие.

Врубка-соединение элементов деревянных конструкций, в которых передача усилия от одного элемента к другому осуществляется путем плотного соприкасания примыкающих плоскостей.

Условие прочности на скалывание

Условие прочности на смятие

50. Кручение бруса круглого сечения. Основные понятия и гипотезы. Вывод формулы касательных напряжений. Анализ формулы. Эпюра в продольных сечениях. Полярный момент сопротивления. Расчеты на прочность.

Вал-брус работающий на кручение.

Кручение- вид нагружения, при котором в поперечных сечениях бруса возникает единственный внутренний силовой фактор - крутящий момент (

Гипотезы:

Сечения плоские до закручивания, остаются плоскими и после закручивания (гипотеза Бернулли)

Все радиусы данного сечения остаются прямыми и поворачиваются на один и тот же угол т.е. каждое сечение поворачивается вокруг оси z как жесткий тонкий диск

Расстояния между сечениями не меняются, значит, продольные волокна не удлиняются и не укорачиваются, т.е. l=const

Возникают только касательные напряжения.

Анализ формулы

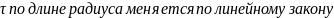
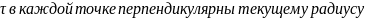
На основании закона о парности такие же напряжения возникают в продольных сечениях

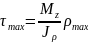
Допускаемое напряжение

51.Кручение-такой вид нагруж. при котором в попереч сеч возникает только крут. момент. (Мz)

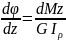
Mz

следовательно

Mpr

dφ м/у двумя близко расположенными сеч равны.

Угол закручения-взаимный угол поворота двух сеч расположенных на расстоянии l.

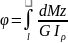dz

Если Мz=const, =const

Для оценки жесткости или дфрм вала,вводят угол θ-относительный угол закруч.

=

Условие жесткости вала:

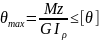
-рад/м.

1. Проверка жесткости.

2.определение несущ. способности.

3.проектный расчет.

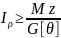=> d≥

Из двух диаметров вала полученных из услов.прочности(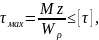

d≥ ) и из усл жесткости выбираем наибольший.

Потенциальная энергия.

Работа затрачиваемая на кручение в пределах упругих дфрм, равна кол-ву потенциальной энергии, накопленной в брусе, и вычисляется как площадь треугольника на диаграмме кручения.

56. Объемное напряженное состояние. Три круга Мора. Наибольшие касательные напряжения. Напряжения на произвольной и октаэдрической площадях. Формулы. Интенсивность напряжений.

При действии σ_{1 ,} σ_{2 ,} σ₃ в точке возникает объемное напряженное состояние. Напряжения на площадках, параллельных одной из осей, определяются как для случая плоского напряженного состояния. Для напряжений σ₁ и σ_{2 ,} σ₂ и σ₃ , σ₃ и σ₁ можно построить круги Мора

Из построений для точки D: τ_max = (σ₁ - σ₂)/2

Нормальные σ и касательные τ напряжения на площадках, параллельных σ₁ , будут характеризоваться кругом напряжений С₂₃, а напряжения на площадках, параллельных σ₂ и σ_3, соответственно кругами С₁₃ и С₁₂. Напряжения на таких площадках определяются как для плоского напряженного состояния.

Можно доказать, что напряжения σ, τ на произвольной площадке определяются по формулам

Точка с координатами D(σ, τ) всегда лежит в заштрихованной области или на ее границе, если площадка не параллельна ни одному из главных напряжений.

Если нормаль к произвольной площадке образует одинаковые углы α1=α2=α3=α с направлениями σ_{1 ,} σ_{2 ,} σ₃ то площадка называется октаэдрической. Для такой площадки cos2 α=1/3 тогда : где σ_окт и τ_окт - октаэдрические напряжения.

Величина, равная называется интенсивностью напряжений.

57. Обобщенный закон Гука. Вывод формулы. Частные случаи. Закон Гука для произвольной площадки.

В общем случае при объемном состоянии действие напряжений σ_{1 ,} σ_{2 ,} σ₃ вызывает деформации в направлении этих напряжений. Данные деформации можно определить на основе принципа независимости действия сил как сумму деформаций по каждому из направлений.

Продольная деформация в направлении σ₁ от действия σ₁ по закону Гука будет:

Уравнение Пуассона:

Деформация - продольная деформация в направлении σ₂, тогда деформация Е₁₂, т.е. по направлению σ₁ от действия σ_{2 ,} будет поперечной по отношению к направлению σ₂ , и из уравнения Пуассона получим:

Аналогично

Полная относительная деформация Е₁ в направлении получается в результате суммирования ε ₁₁, ε ₁₂, ε ₁₃ Эти формулы выражают обобщенный закон Гука. Где ε ₁, ε ₂ , ε ₃ – главные деформации.

При плоском напряженном состоянии σ₃ =0, тогда

При линейном напряженном состоянии σ₂ = σ₃ =0; σ₁= σ

Р ассмотрим элемент dxdydz.

Полные напряжения на гранях представляют нормальными и касательными составляющими. Совокупность этих напряжений носит название тензора напряжений:

Считаем, что нормальные напряжения вызывают линейные деформации ребер dx, dy, dz по направлениям x,y,z – ε _{x ,} ε _{y ,} ε _z

Касательные напряжения вызывают изменения прямых углов, т.е. сдвиговые деформации:

Тогда обобщенный закон Гука для произвольной площадки примет вид:

58. Объемная деформация. Вывод формулы.

Объемная деформация при объемном напряженном состоянии будет θ=(V-V₀)/V₀

Где V₀ = abc-объем до деформации; V- объем после деформации.

Под действием σ_{1 ,} σ_{2 ,} σ₃ стороны параллелепипеда получают удлинение ∆a, ∆d, ∆c. Тогда

Так как ε ₁, ε ₂, ε ₃ малы, то их произведениями пренебрегаем. Тогда объемная деформация будет равна сумме главных деформаций: θ≈ ε₁+ ε₂+ ε_{3 (1)}

Если рассматривать средние значения деформаций и напряжений в виде

(2)

Действующих согласно на октаэдрических площадках, получим: θ=3ε_ср.

Если в формулы (1) и (2) подставить закон Гука , то можно объемную деформацию выразить через напряжения:

Тогда (3)

По уравнению (3) можно оценить предельное значение коэффициента Пуассона- коэффициента поперечной деформации. При положительных σ_ср величина θ должна быть положительна, при отрицательных σ_ср отрицательной должна быть и величина θ , Это возможно, когда:

59. Потенциальная энергия упругой деформации при объемном напряженном состоянии. Частные случаи.

Потенциальная энергия при простом растяжении:

При объемном напряженном состоянии:

Подставим значения ε ₁, ε ₂, ε ₃ по закону Гука :

(1)

Уравнение (1) определяет полную потенциальную энергию, которая включает в себя энергии изменения объема U₀ и формы U_ф тела: U=U₀+U_ф

Объемная деформация θ определяет только энергию изменения объема. Так как величина θ связана с ε_ср и σ_ср , то энергия изменения объема будет: (2)

Если из общей энергии U вычесть энергию изменения объема U₀, то получим энергию формоизменения:

При простом растяжении σ₂ = σ₃ =0,

Чистый сдвиг: σ₂ = τ _, σ₂ = -τ _, σ₂ = 0. По и (2) имеем:

т.е. при чистом сдвиге объем не меняется, и энергия изменения объема равна нулю. Следовательно, потенциальная энергия накапливается только за счет изменения формы

где

60.Траектории главных напряжений при различных напряженных состояниях.

Наглядное представление о потоке внутренних сил в нагруженном теле дают траектории главных напряжений – линии в каждой точке которой касательная совпадает с направлением главного напряжения в этой точке.

1)Простое растяжение – линейное напряженное состояние. Траекториями главных напряжений являются прямые, параллельные и перпендикулярные оси бруса

2) Кручение- плоское напряженное состояние. Траектория главных напряжений представляет винтовую линию, наклоненную под углом 45 к образующей. Прямоугольный элемент в одном направлении испытывает растяжение, в другом -сжатие.

3) Изгиб. Проведем анализ напряженного состояния в разных точках поперечного сечения, ориентируясь на эпюры σ и τ

В точках 1,3-линейное н.с. в точках 5,4-плоское н.с. в точке 2 – плоское н.с.(чистый сдвиг). В каждой точке за исходные принимаются напряжения в поперечном сечении σ и τ , которые находят по формулам:

С помощью круга Мора или по формулам и находят величины главных напряжений σ₁ и σ₂ и их направления.

Двухопорная балка, нагруженная распределенной нагрузкой. Сплошные линии-траектории растягивающих напряжений σ_1, а пунктирные – сжимающих σ₂ . Эти траектории пересекаются между собой под углом 90, а нейтральную ось они пересекают под углом 45.

По траекториям σ₁ можно судить о том, где и в каком направлении могут появиться трещины, если материал плохо работает на растяжение. При армировании железобетонных балок арматуру целесообразно располагать в зонах и по возможности по направлению растягивающих напряжений σ₁ .

11-Как определяются напряжения в поперечных и наклонных сечениях бруса?

Р– сила, равная произведению напряжения на площадь наклонного сечения

®Наибольшие касательные напряжения возникают при угле 45 градусов

®З. парности касат. Напряжений.(на двух взаимно перпендикулярных площадках возникают одинаковые по модулю и разные по направлению касательные напряжения)

Напряжённое состояние в точке

Отношение представляет собой среднее напряжение на площадке 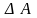. В пределе получаем

,

где –полное напряжение в точке K площади ΔА.

В системе СИ напряжение выражается в паскалях Па=н/м² или мегапаскаляхМПа=10⁶ Па.

Разложим вектор 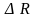по осям координат на составляющие , , и запишем выражения:

, , ,

где – нормальное напряжение; 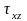и –касательные напряжения.

Тогда напряжение можно рассматривать какполное напряжениевточке на данной площадке:

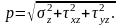
12.з гукапри растяжении сжатииОтносительная продольная деформация прямо пропорциональна соответствующему нормальному напряжению,

Применимость-применим только в упругих деформациях

Графичское представление(з. гука и модуля упругости)

Модуль упругости материала–физ. Смысл (упругая постоянная материала, характеризующая жесткость материала при растяжении)определяется экспериментально

13Растяжение и сжатие -вид нагружения бруса, при котором внутренние силы в поперечном сечении приводятся только к продольной силе N.

Продольная деформация

Формула жёсткости для абсолютной деформации

и 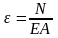.Тогда абсолютное удлинение участка стержня длиной при и будет равно

,

EA - жесткостьстержня при растяжении ,сжатии

Вычесление полного удлинения бруса ,удлинение связанное с температурным воздействием-Если на участке и переменны (рис. 3.9 б), то полное удлинение участка получим, суммируя удлинения бесконечно малых участков dz:

.

Для бруса, имеющего несколько участков:

. (3.14)

Удлинение, связанное с температурным воздействием:

_t^o , (3.15)

где – коэффициент температурного расширения материала; – изменение температуры.

14 Абсолютная и относительная поперечная деформация -Абсолютная поперечная деформация определяется как разность размеров после деформации и до нее:

; .

Относительная поперечная деформация для изотропных материалов по всем направлениям одинакова:

Связь между продольной и поперечной деформациями,коэфпуассона ,его физ и способы определения или

где – коэффициент поперечной деформации (коэффициент Пуассона) – безразмерная величина, упругая постоянная материала, определяемая экспериментально. Для всех изотропных материалов = 0  0,5. Для пробки 0; для каучука  0,5; для стали  0,3.

15.перемещение поперечного сечения при растяжении сжатии 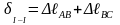(под буквой а )

Диференциальная зависимость м/у перемещением и продольной силой .

Пример построения эпюры-Эпюру перемещений начинают строить от защемленного конца, вычисляя перемещения характерных сечений

Рис. 3.11

I участок,0<z< ₁: ; 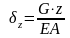(линейный закон), при 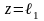перемещение .

II участок,0<z< ₂: , 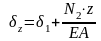; или (const).

Для обеспечения нормальной работы конструкций размеры их элементов необходимо выбирать так, чтобы выполнялось условие жесткости, которое состоит в ограничении упругих перемещений:

(3.19)

где и – наибольшее перемещение; –допускаемое перемещение.

16 Потенциальная энергия упругой деформации-Потенциальной энергией деформации называется энергия, которая накапливается в теле при его упругом деформировании. При статическом нагруженииработа внешних сил полностью преобразуется в потенциальную энергию 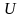, т.е.

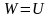
Чтобы судить об энергоемкости материала, вводят понятие удельной потенциальной энергии:

где 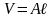– объем стержня.

17краткие сведения о конструкционных материалах

Сталь-сплав железа с углеродо до 2%,если больше 2% то это чугун

Алюминиевые сплавы (дюралюмины,силумины)-сплавы на основе алюминия с добавлением меди ,магния,цинка,марганца)

Медные сплавы(латуни,бронза)-сплавы на основе меди добавлением олова ,цинка,свинца ,никеля ,железа

Древесина-в строительтсве используют хвойную древесину

Композиционные материалы(пластик армированый)-материалы имеющие армириющие элементы

Цель проведения механических испытаний- для определения прочности и жесткости материала.

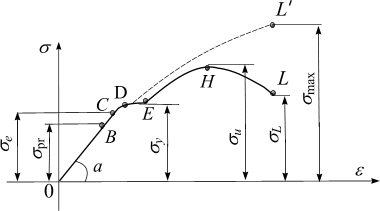
18 диаграмма растяжения низкоуглеродистой стали

Участок ОВ – зона пропорциональности Пределом пропорциональности называется наибольшее напряжение, до которого сохраняется закон Гука.

УчастокОС – зона упругости Пределом упругости называется наибольшее напряжение, до которого остаточная деформация при разгрузке не обнаруживается.

УчастокDЕ- площадка текучести. Пределом текучестиназывается напряжение, при котором образец деформируется без заметного увеличения нагрузки

Характеристики прочности

Все эти напряжения являются характеристикой прочности

На полированном образце появляется сетка полос, наклоненных к оси образца под углом 45⁰, называемых линиями Людерса-Чернова,которая меняет внутренюю структуру материала что приводит к упрочнению .

Образование шейки –в результате растяжения пластичного материала

Вязкое разрушение–края чашечки разрушаются в результате сдвига в направлении наибольших касательных напряжений под углом 45

19.Разгрузка и повторноенагружение

Если вновь нагружать образец, то диаграмма совпадет с линией разгрузки , а дальше пойдет по кривой .

Изучая диаграмму повторного нагружения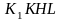 , можно сделать вывод, что свойства металла изменились:

– исчезла площадка текучести;

– предел пропорциональности повысился и стал равным напряжению, до которого первоначально был растянут образец (точка К);

– часть диаграммы, левее , оказалась отсеченной, и остаточное удлинение после разрыва будет меньше на , т.е. материал стал как бы менее пластичным.

Явление повышения упругих свойств материала в результате предварительной пластической деформации называется наклепом.

Условная и истенная диаграммы –пунктиром –истенная(с учетом сужения площади сечения),сплошной линией условная (т.к. при ее построении не учитывается изменение значений площади сечения 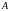в процессе испытания )

У

Величины , , называют упругими характеристиками материала.

20 Характеристики пластичности материалаОтносительное удлинение и относительное поперечное сужение образца после разрыва

Пластичность-свойство материала накапливать до разрушения значительные остаточные деформации

Хрупкость-способность материала разрушаться без образования пластичных деформации