31. Зависимость между моментами инерции относительно параллельных осей.

Пусть известны моменты инерции для фигуры площадью А (рис.6.6) относительно осей х и у (исходные оси). Требуется определить моменты инерции относительно новых осей х₁ и у₁ параллельных исходным.

Рис.6.6

Координаты площадки dA в новой системе координат:

Где а и b- расстояния между исходными и новыми осями.

Пользуясь общими выражениями моментов инерции (6.6) и (6.9), находим

.

Аналогично для момента инерции 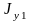. Зависимость для центробежного момента относительно осей x₁ и y₁ примет вид:

Тогда с учетом (6.1), (6.2), (6.6) и (6.9) получим формулы моментов инерции относительно параллельных осей:

(6.12)

Напомним, что в формулах (6.12) геометрические характеристики известны и определены относительно исходных осей х, у. Если эти оси центральные, то , и формулы (6.12) упрощаются:

(6.13)

Формулы (6.13) называют формулами перехода от центральных осей к осям, параллельным им. Из этих формул следуют определения:

Момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между этими осями.

Центробежный момент инерции относительно произвольных осей, параллельных центральным, равен центробежному моменту относительно центральных осей плюс произведение площади сечения на расстояния между осями.

Отметим, что при вычислении моментов инерции по формулам (6.13) расстояния a и b cледует брать с учетом знака в системе координат x₁ и y_1,

Из формул (6.13) следует: из семейства параллельных осей минимальный момент инерции будет относительно центральной оси. Эти формулы часто применяют для вычисления моментов инерции сложных фигур.

32. Моменты инерции простых сечений.

Вычислим моменты инерции п р я м о у г о л ь н и к а относительно центральных осей x и y, параллельных его сторонам (рис. 6.7).

Рис. 6.7

Выделим элементарную площадку в виде узкого прямоугольника . Подставляя значение dA в формулу (6.6) и интегрируя, получим

.

По аналогии можно вычислить и окончательно формулы для осевых моментов инерции относительно центральных осей имеют вид:

. (6.14)

Для осей x₁ и y₁, проходящих через основание, по формулам параллельного переноса (6.13) имеем:

;

; . (6.15)

Центробежный момент инерции , т. к. оси x и y являются осями симметрии.

Вычислим полярный момент инерции к р у г а относительно его центра (рис. 6.8). Выделим бесконечно тонкое кольцо площадь которого равна .

Рис. 6.8

Подставляя значение dA в выражение (6.7) и интегрируя, получим

. (6.16)

На основании выражения 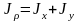и в силу симметрии получим осевые моменты инерции круга:

. (6.17)

Полярный момент инерции к о л ь ц а (рис. 6.9) найдем как разность моментов инерции большого круга диаметром D и малого круга диаметром d:

. (6.18)

Рис. 6.9

Осевые моменты инерции кольца:

. (6.19)

Найдем момент инерции т р е у г о л ь н и к а относительно оси x₁, проходящей через его основание (рис. 6.10).

Рис. 6.10

Разбиваем площадь фигуры на элементарные полоски, параллельные данной оси. Ширина полоски, находящейся на расстоянии у от оси x₁:

.

Тогда площадь полоски:

.

Подставляя dA в формулу (6.6) и интегрируя, получим

.

Окончательно

. (6.20)

Относительно центральной оси x, используя формулу параллельного переноса (6.13), имеем:

;

. (6.21)

Для прокатных профилей (двутавры, швеллеры, уголки и т.д.) моменты инерции и другие геометрические характеристики находят в сортаменте (таблицы прокатных профилей, поставляемых металлургическими заводами в соответствии с требованиями ГОСТов).

33. Зависимости между моментами инерции при повороте осей

Пусть известны моменты инерции произвольного сечения относительно осей x и y (рис. 6.11).

Рис. 6.11

Повернем оси x и y на угол против часовой стрелки по отношению к исходным осям. Найдем моменты инерции относительно повернутых осей x₁ и y_1. Координаты элементарной площадки dA в новых осях:

, .

Найдем момент инерции относительно оси x₁:

Аналогично для и с учетом формул (6.6) и (6.9) окончательно получим:

(6.23)

Складывая почленно формулы (6.22) и (6.23), находим:

. (6.24)

Сумма осевых моментов инерции относительно любой пары взаимно перпендикулярных осей, проходящих через одно начало координат, есть величина постоянная.

Для центробежного момента относительно осей x₁ и y₁:

или после преобразований:

. (6.25)

По формулам (6.22), (6.23), (6.25) находят моменты инерции при повороте осей на угол . Практический интерес представляет поворот осей вокруг центра тяжести.

34. Главные оси и главные моменты инерции

Из формул (6.22) – (6.25) следует, что при повороте осей моменты инерции изменяются, но сумма осевых моментов остается постоянной.

Следовательно, если относительно одной оси значение момента инерции будет наибольшим, то относительно другой – наименьшим. В этом случае центробежный момент относительно этих осей оказывается равным нулю.

Главными центральными осями называются оси, проходящие через центр тяжести и относительно которых центробежный момент равен нулю, а осевые моменты относительно них (осей) обладают свойствами экстремальности и называются главными центральными моментами инерции. Относительно одной главной оси момент инерции имеет наименьшее значение – , относительно другой – наибольшее .

Будем обозначать эти оси буквами u и v. Докажем приведенное утверждение. Пусть оси x и y – центральные оси несимметричного сечения (рис. 6.12).

Рис.6.12

Определим положение главных осей путем поворота центральных осей на угол , при котором центробежный момент становится равным нулю.

.

Тогда из формулы (6.25)

Откуда

. (6.26)

Формула (6.26) определяет положение главных осей, где – угол, на который нужно повернуть центральные оси, чтобы они стали главными. Отрицательные углы откладываются по ходу часовой стрелки от оси x.

Теперь покажем, что относительно главных осей осевые моменты инерции обладают свойством экстремальности. Вычислим производную от выражения (формула 6.22) и приравняем ее к нулю:

(6.27)

Сравнивая выражения (6.27) с (6.25) устанавливаем, что

.

Отсюда следует, что производная обращается в нуль, когда , а это значит, что экстремальные значения имеют моменты инерции относительно главных осей u и v. Тогда по формулам (6.22) и (6.23):

(6.28)

По формулам (6.28) определяются главные центральные моменты инерции.

Если сложить почленно формулы (6.28), то, очевидно, . Если исключить из формул (6.28) угол , то получим более удобную формулу для главных центральных моментов инерции:

. (6.29)

Знак «+» перед вторым слагаемым в (6.29) относится к , знак «-» – к .

Полезно иметь в виду частные случаи:

Если фигура имеет две оси симметрии, то эти оси являются главными центральными осями.

2. Для правильных фигур – равносторонний треугольник, квадрат, круг и т.п., имеющих более двух осей симметрии, все центральные оси являются главными, а моменты инерции относительно них равны между собой.

Умение находить положение главных центральных осей и вычислять и необходимо для определения плоскости наибольшей жесткости сечения (след которой совпадает с осью ) при расчетах на изгиб (глава 7).

35. Общий порядок определения главных центральных

моментов.

Пусть требуется найти положение главных центральных осей и вычислить относительно них моменты инерции для плоского сечения, состоящего из швеллера и полосы (рис. 6.13):

Рис. 6.13

Проводят произвольную систему координат xOy.

Разбивают сечение на простые фигуры и по формулам (6.5) определяют положение центра тяжести С.

Находят моменты инерции простых фигур относительно собственных центральных осей, используя сортамент или по формулам.

Через точку С проводят центральные оси x_c и y_c параллельно осям простых фигур.

Определяют моменты инерции простых фигур относительно центральных осей сечения, используя формулы параллельного переноса (6.13).

Определяют центральные моменты инерции всего сечения как сумму соответствующих моментов простых фигур, найденных в пункте 5.

Вычисляют угол по формуле (6.26) и, поворачивая оси x_c и y_c на угол , изображают главные оси u и v.

По формулам (6.29) вычисляют и .

Делают проверку:

а) ;

б) , если ;

в) .