25) Парабола

В школьном курсе математики достаточно подробно изучалась парабола, которая, по определению, являлась графиком квадратного трехчлена. Здесь мы дадим другое (геометрическое) определение параболы.         Определение 12 . 7   Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки этой плоскости, называемой фокусом , равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.          Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Для этого из фокуса  опустим перпендикуляр   на директрису   . Начало координат   расположим на середине отрезка   , ось   направим вдоль отрезка   так, чтобы ее направление совпадало с направлением вектора   . Ось   проведем перпендикулярно оси   (рис. 12.15).   Рис. 12 . 15 .         Теорема 12 . 4   Пусть расстояние между фокусом   и директрисой   параболы равно   . Тогда в выбранной системе координат парабола имеет уравнение  ( 12 .10)          Доказательство .     В выбранной системе координат фокусом параболы служит точка   , а директриса имеет уравнение  (рис. 12.15). Пусть    -- текущая точка параболы. Тогда по формуле ( 10.4 ) для плоского случая находим  Расстоянием от точки   до директрисы   служит длина перпендикуляра   , опущенного на директрису из точки   . Из рисунка 12.15 очевидно, что  . Тогда по определению параболы   , то есть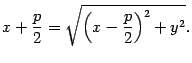  Возведем обе части последнего уравнения в квадрат:  откуда   После приведения подобных членов получим уравнение ( 12.10 ).      Уравнение ( 12.10 ) называется каноническим уравнением параболы.         Предложение 12 . 4   Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью   .          Доказательство .     Проводится так же, как и доказательство  ( предложения 12.1 ).      Точка пересечения оси симметрии с параболой называется вершиной параболы. Если переобозначить переменные  ,   , то уравнение ( 12.10 ) можно записать в виде 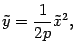  который совпадает с обычным уравнением параболы в школьном курсе математики. Поэтому параболу нарисуем без дополнительных исследований (рис. 12.16).  Рис. 12 . 16 .Парабола         Пример 12 . 6   Постройте параболу   . Найдите ее фокус и директрису. Решение. Уравнение является каноническим уравнением параболы,   ,   . Осью параболы служит ось  , вершина находится в начале координат, ветви параболы направлены вдоль оси  . Для построения найдем несколько точек параболы. Для этого придаем значения переменному   и находим значения   . Возьмем точки   ,   ,  . Учитывая симметрию относительно оси   , рисуем кривую (рис. 12.17)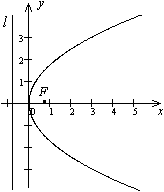  Рис. 12 . 17 .Парабола, заданная уравнением   Фокус  лежит на оси   на расстоянии   от вершины, то есть имеет координаты  . Директриса   имеет уравнение   , то есть   .          Парабола так же, как и эллипс, обладает свойством, связанным с отражением света (рис. 12.18). Свойство сформулируем опять без доказательства.         Предложение 12 . 5   Пусть    -- фокус параболы,    -- произвольная точка параболы,    -- луч с началом в точке   параллельный оси параболы. Тогда нормаль к параболе в точке  делит угол, образованный отрезком   и лучом   , пополам.       Рис. 12 . 18 .Отражение светового луча от параболы Это свойство означает, что луч света, вышедший из фокуса   , отразившись от параболы, дальше пойдет параллельно оси этой параболы. И наоборот, все лучи, приходящие из бесконечности и параллельные оси параболы, сойдутся в ее фокусе. Это свойство широко используется в технике. В прожекторах обычно ставят зеркало, поверхность которого получается при вращении параболы вокруг ее оси симметрии (параболическое зеркало). Источник света в прожекторах помещают в фокусе параболы. В результате прожектор дает пучок почти параллельных лучей света. Это же свойство используется и в приемных антеннах космической связи и в зеркалах телескопов, которые собирают поток параллельных лучей радиоволн или поток параллельных лучей света и концентрируют его в фокусе зеркала. 

26) Определение матрицы. Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов.

Основные понятия матрицы: Числа m и n называются порядками матрицы. В случае, если m=n, матрица называется квадратной, а число m=n - ее порядком.

В дальнейшем для записи матрицы будут применяться обозначение:

Хотя иногда в литературе встречается обозначение:

Впрочем, для краткого обозначения матрицы часто используется одна большая буква латинского алфавита, (например, А), либо символ ||a_ij||, а иногда и с разъяснением: A=||a_ij||=(a_ij) (i=1,2,...,m; j=1,2,...n)

Числа a_ij, входящие в состав данной матрицы, называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j - номер столбца.

Например, матрица    это матрица порядка 2×3, ее элементы a₁₁=1, a₁₂=x, a₁₃=3, a₂₁=-2y, ...

Итак, мы ввели определение матрицы. Рассмотрим виды матриц и дадим соответствующие к ним определения.