6) Линейные операции над векторами в координатной форме
П
ри
умножении вектора на число все его
координаты умножаются на это число,
т.е. если .
Д
ействительно,
используя свойства операций умножения
вектора на число и сложении векторов
будем иметь
.
П
ри
сложении векторов их соответствующие
координаты складываются, т.е. если .
Доказательство очевидно.
Условие коллинеарности двух векторов в коорднинатной форме.
Два
вектора коллинеарны тогда и только
тогда, когда их соответствующие
координаты пропорциональны. Т.е. если 
,
то
.
Доказательство:
Пусть вектор
коллинеарен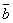 
,
тогда найдется λ такое, что 
.
Значит, 
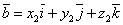и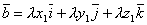 
.
Поскольку разложение вектора по
элементам базиса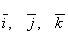 
единственно,
то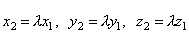 
.П
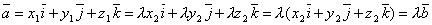усть
выполняется равенство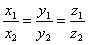 
.
Обозначим коэффициент пропорциональности
через λ. Тогда
и,
следовательно, ,
т.е.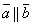 
.
Теорема доказана.
Действия с векторами в координатной форме
Пусть
– базис векторного пространства V над
полем K и 
–
произвольный вектор векторного
пространства V. Из определения базиса
следует, что любой вектор
можно
представить в виде линейной комбинации
базисных векторов и притом единственным
образом:
.
(1)
Определение.
Равенство (1) называется разложением
вектора х по базису
.
Коэффициенты линейной комбинации
(1): 
называются
координатами вектора х относительно
базиса
.
Теорема. Пусть – базис векторного пространства V над полем K. Отображение
,
которое
каждому вектору
ставит
в соответствие упорядоченный набор 
его
координат относительно данного базиса
является биекцией, т.е. взаимно однозначным
соответствием.
Доказательство.
Для каждого вектора векторного
пространства V существует единственный
набор его координат, поэтому
соответствие 
является,
по определению, отображением.
Докажем, что отображение является сюръекцией. Пусть – произвольный набор скаляров. Тогда положим, по определению,
.
Так как V – векторное пространство над полем K, то произведение базисных векторов на скаляры поля K являются векторами векторного пространства V:
, 
.
Сумма векторов векторного пространства V также является его вектором, т.е.
.
Таким образом, для любого упорядоченного набора из n скаляров поля K существует вектор , для которого этот набор скаляров является его координатами относительно данного базиса, т.е.
,
ч.т.д.
Докажем, что отображение является инъекцией.
Пусть, 
–
два произвольных вектора векторного
пространства и 
.
Мы хотим доказать, что 
.
Допустим противное, что различным
векторам отображение
ставит
в соответствие один и тот же набор
скаляров:
.
Из определения отображения следует, что этот набор скаляров является координатами как вектора х, так и вектора у относительно базиса , т.е.
и 
,
откуда следует, что 
.
Получили противоречие, следовательно,
различные векторы имеют различные
координаты и
,
ч.т.д.
Таким образом, отображение является инъекцией и сюръекцией, т.е. биекцией, ч.т.д.
Теорема доказана.
Замечание. В дальнейшем, координаты вектора х будем записывать столбцом и обозначать:
.
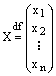В соответствии с обозначениями предыдущей теоремы, будем писать:
.
В этих обозначениях справедлива следующая теорема.
Теорема. Пусть относительно фиксированного базиса векторного пространства V над полем K
, 
,
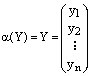где 
–
произвольные векторы, и пусть 
–
произвольный скаляр. Тогда справедливы
равенства:
1) 
или
;
2) 
или
.
Другими словами, при сложении векторов их координаты складываются, а при умножении скаляра на вектор его координаты умножаются на этот скаляр.
Доказательство. Пусть
, 
.
Складывая вектора х и у, и умножая вектор х на скаляр , получаем:
,
.
Отсюда,
, 
,
ч.т.д.
Теорема доказана.
Векторы
Обозначения: 
Длина
вектора, модуль (абсолютная величина): 
Сумма векторов:
(правило
треугольника) (рис. 1.22);
(правило
параллелограмма) (рис. 1.23);
(правило
многоугольника);
(правило
параллелепипеда, 
-
диагональ).
Разность
векторов: 
Формула
вычитания векторов: 
(рис.
1.24).
Признак
коллинеарности векторов: 
7) Скалярное произведение векторов и его свойства
Скалярным
произведением двух ненулевых векторов
называется число, равное произведению
длин этих векторов на косинус угла
между ними. Если хотя бы один из двух
векторов нулевой, то угол между ними
не определён, а скалярное произведение
считается равным нулю. Скалярное
произведение векторов 
и 
обозначается
(1.7)
где 
—
величина угла между векторами
и
(см.
рис. 1.22 в разд. 1.6).
Скалярное
произведение вектора самого на
себя 
называется
скалярным квадратам.
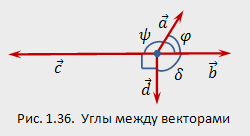
Пример
1.13. Найти скалярные произведения ,
если известно, что 
,
угол
между
векторами
и
равен 
, 
,
а вектор 
образует
с вектором
угол 
(рис.1.36).
Решение. По определению находим
Так
как векторы
и 
противоположно
направленные, то угол 
между
векторами
и
равен 
.
Поэтому
Угол
между противоположно направленными
векторами
и
равен 
,
поэтому
Вектор
ортогонален
вектору
(и
вектору
),
так как величина угла между ними равна 
,
а 
.
Поэтому 
.Угол 
между
векторами
и
равен 
,
поэтому 
8)
Скалярное
произведение векторов. Он-лайн
калькуляторы скалярного произведения
и угла между векторами по координатам.
Скалярное произведение векторов - это операция над двумя векторами, результатом которой является число (не вектор).
Определяется скалярное произведение, как правило, следующим образом:
|
|
Иными словами, скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними . Необходимо заметить, что угол между двумя векторами - это угол, который они образуют, если отложить их от одной точки, то есть начала векторов должны совпадать.
Непосредственно из определения следуют следующие простейшие свойства:
1
. Скалярное
произведение произвольного вектора а
на себя же (скалярный
квадрат вектора а) всегда
неотрицательно, и равно квадрату длины
этого вектора. Причем скалярный квадрат
вектора равен нулю тогда и только тогда,
когда данный вектор - нулевой.
2.Скалярное произведение любых перпендикулярных векторов a и b равно нулю.
3. Скалярное произведение двух векторов равно нулю тогда и только тогда, когда они перепендикулярны или хотя бы один из них - нулевой.
4. Скалярное произведение двух векторов a и b положительно тогда и только тогда, когда между ними острый угол.
5.Скалярное произведение двух векторов a и b отрицательно тогда и только тогда, когда между ними тупой угол.