43) Размерность и базис линейного пространства, координаты вектора
Пусть X — линейное пространство.
Определение. Если существует натуральное число n такое, что X содержит линейно независимую систему из n векторов, а любая система из n + 1 вектора линейно зависима, то X называется n –мерным линейным пространством, а число n – его размерностью.
Будем обозначать n –мерное линейное пространство Xn , где n = dimXn — размерность пространства Xn .
Из определения следует, что размерность линейного пространства равна максимальному количеству линейно независимых векторов.
Замечания.
Размерность пространства, состоящего только из одного нулевого вектора, равна нулю. Такое пространство называется тривиальным.
Если в линейном пространстве существует любое число линейно независимых векторов, то такое пространство называетсябесконечномерным. Мы будем рассматривать, в основном, конечномерные линейные пространства. Бесконечномерные пространства являются предметом специального изучения.
Определение. Упорядоченная система векторов e1, e2, … , en X называется базисом в X , если
система векторов e1, e2, … , en линейно независима;
любой вектор x пространства X может быть представлен в виде
x = ξ1e1 + ξ2e2 + … + ξnen.
(1)
Выражение (1) называется разложением вектора x по базису e1, e2, … , en .
Коэффициенты ξ1, ξ2, … , ξn в разложении векторапо данному базису определяются однозначно.
Коэффициенты разложения (1) вектора x по базису e1, e2, … , en называются координатами вектора x в этом базисе.
Удобно использовать обозначение для i –ой координаты ξi = ei, x и для вектора x = {ξ1, ξ2, … , ξn} . Координаты вектора записывают также в виде матрицы–столбца
ξ1
ξ2
…
ξn
который называется координатным столбцом вектора x .
В n–мерном линейном пространстве Xn существует базис. Он содержит n векторов.
Замечания.
1. В линейном пространстве существует бесчисленное множество базисов.
2. В бесконечномерном пространстве всегда существует базис. Он содержит бесконечное множество векторов.
3. Любая упорядоченная линейно независимая система из n векторов в n–мерном пространстве является базисом.
Теорема. Пусть Xn — линейное пространство и e1, e2, … , en — некоторый базис в Xn . Тогда:
При сложении векторов их координаты складываются.
При умножении вектора на число его координаты умножаются на это число.
Утверждения теоремы в наших обозначениях выглядят следующим образом:
ei, x + y = ei, x + ei, y ;
ei, αx = αei, x .
44) Разложение вектора по базису
п.2. Разложение вектора по базису.
Определение.
Пусть 
–
произвольный вектор, 
–
произвольная система векторов.
Если выполняется равенство
,
(1)
то
говорят, что вектор
представлен
в виде линейной комбинации
данной системы векторов.
Если данная система векторов
является
базисом векторного пространства,
то равенство (1)
называется разложением вектора
по
базису
. Коэффициенты
линейной комбинации 
называются
в этом случае координатами
вектора
относительно
базиса
.
Теорема. (О разложении вектора по базису.)
Любой вектор векторного пространства можно разложить по его базису и притом единственным способом.
Доказательство.
1) Пусть L произвольная прямая (или ось)
и 
–базис 
.
Возьмем произвольный вектор 
.
Так как оба вектора 
и
коллинеарные
одной и той же прямой L,
то 
.
Воспользуемся теоремой о
коллинеарности двух векторов.
Так как 
,
то найдется (существует) такое число 
,
что 
и
тем самым мы получили разложение
вектора
по
базису
векторного пространства
.
Теперь докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису векторного пространства :
и 
,
где 
.
Тогда 
и
используя закон дистрибутивности,
получаем:
.
Так
как
,
то из последнего равенства следует,
что 
,
ч.т.д.
2)
Пусть теперь Р произвольная плоскость и 
– базис 
.
Пусть 
произвольный
вектор этой плоскости. Отложим все три
вектора от какой-нибудь одной точки
этой плоскости. Построим 4 прямых.
Проведемпрямую 
,
на которой лежит вектор
, прямую 
,
на которой лежит вектор 
.
Через конец вектора
проведем прямую параллельную
вектору
и
прямую параллельную вектору
.
Эти 4 прямые высекают
параллелограмм. См. ниже рис. 3. По правилу
параллелограмма 
,
и 
, 
,
– базис
, 
– базис
.
Теперь,
по уже доказанному в первой части этого
доказательства, существуют такие числа 
,
что
и 
.
Отсюда получаем:
и
возможность разложения по базису
доказана.
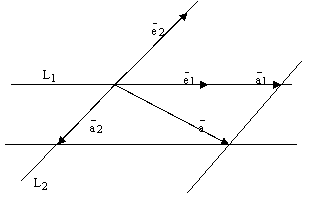
рис.3.
Теперь
докажем единственность разложения по
базису. Допустим противное. Пусть
имеется два разложения вектора
по
базису
векторного пространства
: 
и 
.
Получаем равенство
,
откуда следует 
.
Если 
,
то 
,
а т.к. 
,
то 
и
коэффициенты разложения равны: 
, 
.
Пусть теперь 
.
Тогда 
,
где 
.
По теореме о коллинеарностидвух векторов отсюда
следует, что 
.
Получили противоречие условию теоремы.
Следовательно,
и
,
ч.т.д.
3)
Пусть 
– базис 
и
пусть 
произвольный
вектор. Проведем следующие построения.
Отложим
все три базисных вектора 
и
вектор
от
одной точки и построим 6 плоскостей:
плоскость, в которой лежат
базисные векторы 
, плоскость 
и плоскость 
;
далее через конец вектора
проведем
три плоскости параллельно
только что построенным трем плоскостям.
Эти 6 плоскостей высекают
параллелепипед:
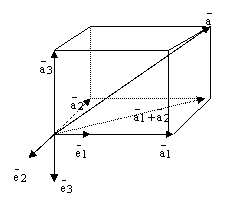
рис.4.
П
о
правилу сложения векторов получаем
равенство:
.
(1)
По
построению 
.
Отсюда, по теореме о коллинеарности двухвекторов,
следует, что существует число 
,
такое что 
.
Аналогично,
и 
,
где 
.
Теперь, подставляя эти равенства в (1),
получаем:
(2)
и возможность разложения по базису доказана.
Докажем единственность такого разложения. Допустим противное. Пусть имеется два разложения вектора по базису :
и 
.
Тогда
.
(3)
Заметим, что по условию векторы некомпланарные, следовательно, они попарно неколлинеарные.
Возможны два случая: или .
а) Пусть , тогда из равенства (3) следует:
.
(4)
Из
равенства (4) следует, что
вектор
раскладывается
по базису 
,
т.е. вектор
лежит
в плоскости векторов
и,
следовательно, векторы
компланарные,
что противоречит условию.
б)
Остается случай
,
т.е. 
.
Тогда из равенства (3) получаем 
или
.
(5)
Так
как
– базис пространства векторов лежащих
в плоскости, а мы уже доказали
единственность разложения по
базису векторов плоскости,
то из равенства (5) следует, что
и 
,
ч.т.д.
Теорема доказана.
45) Линейное подпространство линейного пространства
Определение. Множество
M векторов линейного пространства L,
такое, что для любых 
и 
из
M и любого числа справедливо 
,
назвается линейным подпространством
линейного пространства L.
Пример. Множество M арифметических векторов из Rn, у которых последние компоненты — нулевые, образует линейное подпространство в Rn:
Можно
доказать, что если M — линейное
подпространство линейного пространства
L, то нулевой элемент пространства L
принадлежит M и если 
,
то и 
.
Справедливо следующее утверждение
Линейное подпространство линейного пространства является линейным пространством.
2.7. Преобразование координат вектора при переходе к новому базису
Пусть 
и 
—
два базиса в n-мерном
линейном пространстве L.
Матрицей перехода от базиса к базису называется матрица C, столбцами которой являются координаты векторов в базисе :
Вектор 
линейно
выражается через векторы обоих базисов.
Тогда, если 
то координаты 
вектора
в базисе
,
и его координаты 
в
базисе
связаны
соотношениями
,
или 
где 
, 
—
матрица перехода от базиса
к
базису
и
обратная к ней; 
—
векторы-столбцы координат вектора
в
соответствующих базисах.
Таким образом доказана следующая
Теорема. Пусть (e)={ } и (f)={ }— два базиса в n-мерном линейном пространстве L.
Координаты 
вектора
в
базисе (e) и
координаты 
вектора
в
базисе (f)связаны
соотношением
где , — матрица перехода от базиса (e) к базису (f) и обратная к ней.