Правила дифференцирования

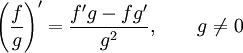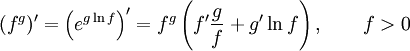При дифференцировании константу можно выносить за производную: Правило дифференцирования суммы функций: Правило дифференцирования разности функций: Правило дифференцирования произведения функций (правило Лейбница): Правило дифференцирования частного функций: Правило дифференцирования функции в степени другой функции: Правило дифференцирования сложной функции

Сложная функция (композиция функций, суперпозиция функций) обозначается или .

Производная композиции равна:

Если необходимо взять производную от композиции трех и более функций, то последовательно применяем указанное выше правило. Например,

Правило логарифма при дифференцировании функции:

21)Производные высших порядков

Производные высшего и дробного порядка

Другое простое обобщение, которое можно произвести, — это применить её больше, чем один раз, получая в результате производную второго (и выше) порядка, как определено в статье о производных. Этот способ может быть обобщён.

В добавок к производным n-ого порядка для любого натурального числа n, используя различные методы, возможно ввести производные в дробных степенях, получая при этом так называемые производные дробного порядка. Производные отрицательных порядков будут соответствовать интегрированию, откуда появляется термин дифферинтеграл. Изучение различных возможных определений и записей производных ненатуральных порядков известно под названием дробное исчисление.

Производные высших порядков

Если функция дифференцируема при всех , то мы можем рассмотреть функцию , сопоставляющую каждой точке значение производной . Эта функция называется производной функции , или первой производной от . (Иногда саму исходную функцию называют нулевой производной и обозначают тогда .) Функция , в свою очередь, может иметь производную во всех (или некоторых) точках интервала , которую мы обозначим и назовём второй производной функции . Если предположить, что вторая производная существует во всех точках , то она может также иметь производную , называемую третьей производной функции , и т. д. Вообще, -й производной функции называется производная от предыдущей, -й производной :

если эта производная существует. -я производная называется также производной -го порядка, а её номер называется порядком производной.

При первую, вторую и третью производные принято обозначать штрихами: или ; при прочих  -- числом в скобках в верхнем индексе: или .

Физический смысл производной второго порядка проясняется из того, что если первая производная задаёт мгновенную скорость изменения значений в момент времени , то вторая производная, то есть производная от , задаёт мгновенную скорость изменения значений мгновенной скорости, то есть ускорение значений . Следовательно, третья производная -- это скорость изменения ускорения (или, что то же самое, ускорение изменения скорости, поскольку, как очевидно следует из определения, ).

22)Дифференциалы высших порядков Дифференциалом порядка n, где n > 1 от функции   в некоторой точке называется дифференциал в этой точке от дифференциала порядка (n — 1), то есть

  .